总结——关系数据理论

Posted 2022-11-25 Fmm-PMO

全是理论<很费脑子>的一章结束了，这样一章主要涉及了一个很基本的问题：针对一个具体问题，应该如何构造一个适合于它的数据库模式，即应该构造几个关系模式，每个关系由哪些属性组成等。

📋目录
    前言
一、规范化
    1.函数依赖
    2.平凡函数依赖与非平凡函数依赖
    3.完全函数依赖与部分函数依赖
    4.传递函数依赖
    5.码
    6.范式
    7.多值依赖
    8.规范化小结
二、候选码的求解理论和算法
    用闭包求解之前的例题中的找候选码问题
三、规范化总结
四、课程感悟

前言：

❖关系模式由五部分组成，是一个五元组：R(U, D, DOM, F)

R是符号化的元组语义
U为一组属性
D为属性组U中的属性所来自的域
DOM为属性到域的映射
F为属性组U上的一组数据依赖

D、DOM与模式设计关系不大，只用到三元组：R<U,F>
二维表每个分量必须是不可分开的数据项。
满足了这个条件的关系模式就属于：第一范式（1NF）

❖数据依赖
    ◼是一个关系内部属性与属性之间的一种约束关系
    ◼通过属性间值的相等与否体现出来的数据间相互联系
    ◼是现实世界属性间相互联系的抽象
    ◼是数据内在的性质
    ◼是语义的体现。
❖主要类型:
    ◼函数依赖（Functional Dependency，简记为FD）
    ◼多值依赖（Multi-Valued Dependency，简记为MVD）

函数依赖普遍存在于现实生活中：
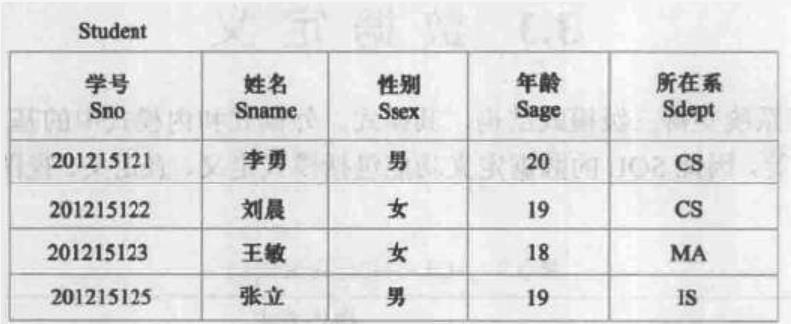
    描述一个学生关系，可以有学号、姓名、系名等属性。
        ◼一个学号只对应一个学生，一个学生只在一个系中学习
        ◼“学号”确定后，学生姓名及所在系的值就被唯一确定。

    Sname=f(Sno)，Sdept=f(Sno)
        ◼Sno函数决定Sname
        ◼Sno函数决定Sdept
        ◼记作：Sno→Sname，Sno→Sdept

未经加工的普通的关系模式通常由以下缺点disadvantages，相应的，这样的模式也就不是一个好的模式。

（1）数据冗余

浪费大量的存储空间:有些数据重复出现

（2）更新异常（Update Anomalies）

更新数据时，维护代价大:某系更换重复出现的数据后，须修改有关的每一个元组。

（3）插入异常（Insertion Anomalies）

（4）删除异常（Deletion Anomalies）

一、规范化

1.函数依赖

设R(U)是一个属性集U上的关系模式，X和Y是U的子集。
若对于R(U)的任意一个可能的关系r，r 中不可能存在： 两个元组在X上的属性值相等，而在Y上的属性值不等（可理解为两个元组在X上的属性值相等，则在Y上的属性值也一定相等）， 则称“X函数确定Y”或“Y函数依赖于X”，记作X→Y。若X→Y，并且Y→X, 则记为X←→Y。
若Y不函数依赖于X, 则记为X→Y。

举个栗子：

[例] Student(Sno, Sname, Ssex, Sage, Sdept),假设不允许重名，则有:Sno → Ssex，Sno → Sage，Sno → Sdept， Sno ←→ Sname，Sname → Ssex，Sname → Sage，Sname → Sdept，但Ssex →Sage, Ssex→ Sdept。

2.平凡函数依赖与非平凡函数依赖

（平凡函数依赖都是必然成立的，不反映新的语义。后边讨论的不出意外都是非平凡函数依赖）

X→Y，但Y⊈X则称X→Y是非平凡的函数依赖。
X→Y，但Y⊆X 则称X→Y是平凡的函数依赖。

若X→Y，则X称为这个函数依赖的决定因素

3.完全函数依赖与部分函数依赖

在R(U)中，如果X→Y，并且对于X的任何一个真子集X’, 都有 X’ ↛ Y, 则称Y对X完全函数依赖，记作$X\stackrel{F}{\to }Y$。若X→Y，但Y不完全函数依赖于X，则称Y对X部分函数依赖，记作$X\stackrel{P}{\to }Y$

举个栗子：
[例] 在关系SC(Sno, Cno, Grade)中，有：Sno ↛Grade，Cno ↛ Grade，
因此：$(Sno,Cno)\to /Grade$
$(Sno,Cno)\stackrel{P}{\to }Sno$
$(Sno,Cno)\stackrel{P}{\to }Cno$

4.传递函数依赖

在R(U)中，如果X→Y(Y⊈X)，Y↛X，Y→Z，Z⊈Y, 则称Z对X传递函数依赖。记为：X → Z。

PS：注: 如果Y→X, 即X←→Y，则Z直接依赖于X，而不是传递函数依赖。

举个栗子：
[例] 在关系Std(Sno, Sdept, Mname)中，有：
Sno → Sdept，Sdept → Mname，
Mname传递函数依赖于Sno

5.码

设K为R<U,F>中的属性或属性组合。若K → U，则K称为R的一个 候选码
如果U部分函数依赖于K，即K → U,则K称为超码 。
候选码是最小的超码，即K的任意真子集都不是候选码。
若关系模式R有多个候选码，则选定其中的一个做为主码(Primary key)。

主属性与非主属性
    ◼包含在任何一个候选码中的属性 ，称为主属性
    ◼不包含在任何码中的属性称为非主属性
    ◼整个属性组是码，称为全码（All-key）
举个栗子：
[例]S(Sno, Sdept, Sage)，单个属性Sno是码
SC(Sno, Cno, Grade)中，属性组(Sno, Cno)是码
[例] R(P,W,A) P：演奏者 W：作品 A：听众
一个演奏者可以演奏多个作品，某一作品可被多个演奏者演奏，听众可以欣赏不同演奏者的不同作品
为了唯一确定唯一的一个元组，需要同时确定演奏者，作品，听众，所以码为(P,W,A)，即All-Key
关系模式 R中属性或属性组X 并非 R的码，但 X 是另一个关系模式的码，则称 X 是R 的外部码（Foreign key）也称外码
[例]SC(Sno,Cno,Grade)中，Sno不是码。Sno是 S(Sno,Sdept,Sage)的码，则Sno是SC的外码

6.范式

范式是符合某一种级别的关系模式的集合。
各种范式之间存在联系：某一关系模式R为第n范式，可简记为R∈nNF。
一个低一级范式的关系模式，通过模式分解可以转换为若干个高一级范式的关系模式的集合，这种过程就叫规范化

第一范式（1NF）
二维表每个分量必须是不可分开的数据项。满足了这个条件的关系模式就属于1NF

第二范式（2NF）
关系模式R∈1NF，并且每一个非主属性都完全函数依赖于任何一个候选码
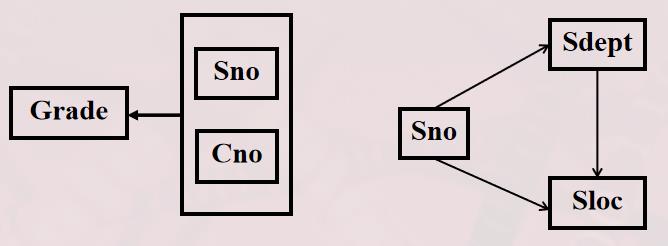
[例] S-L-C(Sno,Sdept,Sloc,Cno,Grade)， Sloc为学生的住处，并且每个系的学生住在同一个地方。S-L-C的码为(Sno,Cno)。
函数依赖有

(Sno,Cno)→Grade
Sno→Sdept, (Sno,Cno)→Sdept
Sno→Sloc, (Sno,Cno)→Sloc
Sdept→Sloc

    ◼非主属性Sdept、Sloc并不完全依赖于码
    ◼关系模式S-L-C不属于2NF

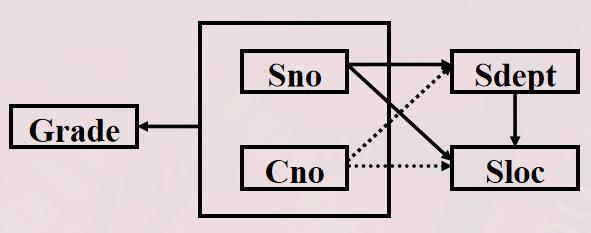
既然不是2NF，那么如何将其进行转换，使其成为2NF呢？
该例子中有两个非主属性，一类如Grade，它对码完全函数依赖，另一类如Sdept、Sloc，它们对码不是完全函数依赖
用投影分解把关系模式S-L-C分解成两个关系模式

SC(Sno,Cno,Grade)
S-L(Sno,Sdept,Sloc)

此时SC的码为(Sno,Cno),SL的码为Sno，就实现了完全函数依赖。

第三范式（3NF）
设关系模式R<U,F>∈1NF，若R中不存在这样的码X，属性组Y及非属性组Z（Z ⊉ Y）使得X→Y，Y→Z成立，Y↛ X，则称R<U,F>∈3NF

还拿刚才的栗子，SC没有传递依赖，因此SC ∈ 3NF
S-L中Sno →Sdept( Sdept ↛ Sno), Sdept→Sloc，可得Sno → Sloc。
解决的办法是将S-L分解成（一言不合分解就完事了！）

S-D(Sno,Sdept)∈ 3NF
D-L(Sdept,Sloc)∈ 3NF

BCNF
通常认为BCNF是修正的第三范式，有时也称为扩充的第三范式。关系模式R<U，F>∈1NF，若X → Y且 Y ⊈ X 时X必含有码，则R<U,F>∈BCNF。即在R中，每一个决定因素都包含码。
一个满足BCNF的关系模式有：

所有非主属性对每一个码都是完全函数依赖
所有主属性对每一个不包含它的码也是完全函数依赖
没有任何属性完全函数依赖于非码的任何一组属性。

由于R∈BCNF，按定义排除了任何属性对码的传递依赖与部分依赖，所以R∈3NF，但若R属于3NF，R未必属于BCNF。
举例如下：

属于BCNF的
考察关系模式C(Cno,Cname,Pcno)

1.C只有一个码Cno，非主属性：Canme，Pcno
2.没有非主属性对Cno部分依赖或传递依赖，所以C∈3NF。
3.C中Cno是唯一的决定因素，所以C∈BCNF。

不属于BCNF的
关系模式STJ(S,T,J)中，S表示学生，T表示教师，J表示课程。每一教师只教一门课。每门课有若干教师，某一学生选定某门课，就对应一个固定的教师。
由语义可得到函数依赖：(S,J)→T；(S,T)→J；T→J
候选码：（S,J），（S,T）；没有非主属性
因为没有非主属性对码传递依赖或部分依赖，STJ ∈ 3NF。
因为T是决定因素，而T不包含码，所以STJ不是 BCNF范式。

BCNF的关系模式也可以通过分解成为BCNF。
例如STJ可分解为ST(S,T)与TJ(T,J)，它们都是BCNF。

7.多值依赖

设R(U)是属性集U上的一个关系模式。X,Y,Z是U的子集，并且Z=U-X-Y。关系模式R(U)中多值依赖X→→Y成立，当且仅当对R(U)的任一关系r，给定的一对(x,z)值，有一组Y的值，这组值仅仅决定于x值而与z值无关。
【例】 Teaching（C, T, B）（C代表课程，如物理；T代表教师；B代表参考书，如普通物理）
Teaching具有唯一候选码(C,T,B)， 即全码。Teaching∈BCNF
对于C的每一个值，T有一组值与之对应，而不论B取何值。
因此T多值依赖于C，即C→→T

平凡多值依赖和非平凡的多值依赖
    若X→→Y，而Z＝Ф，则称X→→Y为平凡的多值依赖。
    否则称X→→Y为非平凡的多值依赖。

4NF
关系模式R<U,F>∈1NF，如果对于R的每个非平凡多值依赖X→→Y（Y ⊈ X），X都含有码，则R<U,F>∈4NF。如果一个关系模式是4NF， 则必为BCNF，因为每个决定因素都包含码。
不是4NF的，同样可以通过模式分解的方式将其化为4NF。

8.规范化小结

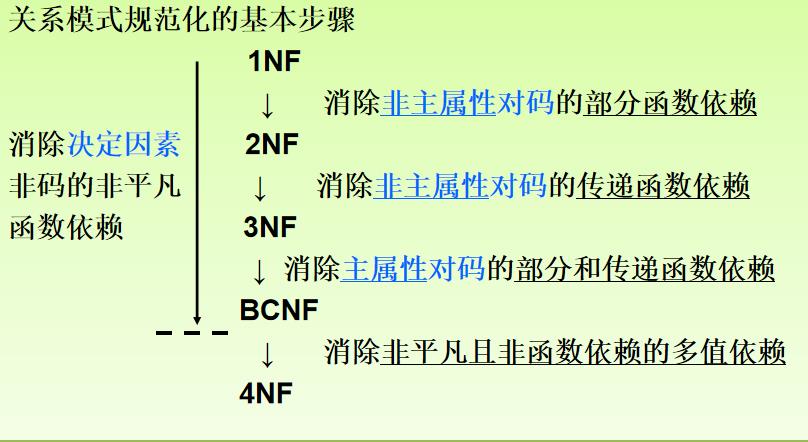
二、候选码的求解理论和算法

闭包（记作X＋ ）就是由一个属性直接或间接推导出的所有属性的集合。

例如：
f=a->b，b->c，a->d，e->f；由a可直接得到b和d，间接得到c，则a的闭包就是a，b，c，d
对于给定的关系R（A1，A2，…An）和函数依赖集F，可将其属性分为4类：
    L类 仅出现在函数依赖左部的属性。
    R 类 仅出现在函数依赖右部的属性。
    N 类 在函数依赖左右两边均未出现的属性。
    LR类 在函数依赖左右两边均出现的属性。

定理：
对于给定的关系模式R及其函数依赖集F，若X（X∈R）是L类属性，则X必为R的任一候选码的成员。

推论：
对于给定的关系模式R及其函数依赖集F，若X（X∈R）是L类属性，且X+包含了R的全部属性；则X必为R的唯一候选码。

例：
设有关系模式R（A，B，C，D），其函数依赖集F=D→B，B →D，AD →B，AC →D，求R的所有候选码。

解：
考察F发现，A，C两属性是L类属性，所以AC必是R的候选码成员，又因为（AC）+=ABCD，所以AC是R的唯一候选码。

定理：对于给定的关系模式R及其函数依赖集F，
若X（X∈R）是R类属性，则X不在任何候选码中。

定理：对于给定的关系模式R及其函数依赖集F，
若X（X∈R）是N类属性，则X必包含在R的任一候选码中。

推论：对于给定的关系模式R及其函数依赖集F，
若X（X∈R）是L类和N类组成的属性集，且X+包含了R的全部属性；则X是R的唯一候选码。

【例 1】
设关系模式 U=(A , B , C , D ),函数依赖集 F=D→ B , B → D , AD → B , AC → D, 求 U 的候 选码。
解：
(1) L=(A , C), R=空, LR=(B , D), N=空;
(2) L∪N=(A , C), 因为(AC) + = ACBD = U,
AC 是唯一候选码
【例2】
R<U,F>,U=(A,B,C,D,E,G),F=AB→C,CD→E,E→A，A→G,求候选码。
解:
(1) L=(B,D), R=(G), LR=(A,C,E ), N=空;
(2) L∪N=(B,D), (BD)+=BD;
(3)ABD：AB→C,CD→E, A→G,
所以(ABD)+ = ABDCEG = U BDC：CD→E, E→A, A→G
所以(BDC)+ = BDCEAG = U BDE：E→A, A→G, AB→C,
所以(BDE)+ = BDEAGC = U
候选码有3个分别是ABD、BCD和BDE

【例3】

这是一种特殊的情况，之前讨论的是没有等价等情况的，所以如果找到了含有2个属性的候选码，那么就不再找含有3个的，4个的，但当有等价等特殊情况时，就要再考虑，其实我觉得有一个避免漏找的方法：就是先从L和N的并集中找，然后和LR中的属性组合，直到所有的LR中属性都被考虑。

设关系模式 U=(A , B , C , D , E , F ),
函数依赖集
F=A→BC , BC→A , BCD→EF , E→C,
求 R 的候选码。
解:
(1) L=(D), R=(F), LR=(A , B , C , E ), N=空;
(2) L∪N=(D) , D+=D;
(3)因为 (DA)+=DABCEF=U, (DB)+=DB ,(DC)+=DC, (DE)+=DEC, 所以 DA 是候选码;
(4)因为 (DBC)+=DBCAEF=U, (DBE)+=DBECAF=U, (DCE)+=DCE, 所以DBC、DBE 是候选码;
(5) U 的候选码有 DA、DBC、DBE（A←→BC）

既然学了闭包，那么就来用一下吧，下面以这篇博客中例题中的求候选码的部分用闭包方式进行求解。

①
Y(X1,X2,X3,X4)
(X1,X2)→X3
X2→X4

L = (X1,X2)；R = (X3,X4)；LR = 空；N = 空
L∪N = （X1,X2）
（X1,X2）+ = X1X2X3X4 = U；所以候选码为（X1,X2）

②
R（A，B，C，D）
F=AB→D，AC→BD，B→C

L = （A,）; R = （D）；LR = （B,C）；N = 空
L∪N = （A）；
（A）+ = A
（AB）+ = ABCD = U；为候选码
（AC）+ = ABCD = U；为候选码
所以候选码为（A,B）和（A,C）

③
R（X，Y，Z，W）
F=Y←→W，XY→Z

L = （X,）；R = （Z）；LR = （Y,W）；N = 空
L∪N = （X）；
（X）+ = X
（XY）+ = XYZW = U；为候选码
（XW）+ = XYZW = U；为候选码
所以候选码为（X,Y）和（X,W）

④
R（A,B,C,D,E） F=A→B,CE→A,E→D

L = （C,E）；R = （B,D）；LR = （A,）；N = 空
L∪N = （C,E）
（CE）+ = ABCDE = U
所以候选码为（C,E）

⑤
R(商店编号，商品编号，数量，部门编号，负责人)
每个商店的每种商品只在一个部门销售，
每个商店的每个部门只有一个负责人
每个商店的每种商品只有一个库存数量

R（A,B,C,D,E），且有F=AB→D,AD→E,AB→C
L = （A,B,）；R = （C,E）；LR = （D,）；N = 空
L∪N = （A,B）
（AB）+ = ABCDE = U；为候选码

⑥
R(A,B,C,D,E,F) F=A→C,AB→D,C→E,D→BF

L = （A,）；R = （E,F）；LR = （B,C,D）；N = 空
L∪N = （A）
（A）+ = ACE ≠U
（AB）+ = （ABCDEF）= U；为候选码
（AC）+ = （ACE）≠U
（AD）+ = （ABCDEF）= U；为候选码
所以候选码为（A,B）和（AD）

三、规范化总结

不能说规范化程度越高的关系模式就越好。必须对现实世界的实际情况和用户应用需求作进一步分析，确定一个合适的、能够反映现实世界的模式。上面的规范化步骤可以在其中任何一步终止。

四、课程感悟

这一章的内容还蛮复杂的，需要花费时间去想，去思考，同时也考虑严谨性，不能漏掉情况，相较于前面章节的学习还是有点挑战性的，尤其是模式拆分和候选码的查找，需要多加练习，熟能生巧！