零知识证明|3.什么是KCA系数知识假设？

Posted 2022-11-23 TurkeyCock

上一篇介绍了盲计算，所谓盲计算，就是Alice在不知道s的情况下完成多项式计算。

那么，Bob如何确定Alice的计算结果是正确的呢？要实现这一目标，需要先介绍一个概念：α对。

在有限循环群G中，如果$\alpha ,\beta ̸=0且b=\alpha \cdot a$，那么就称$(a,b)$为一个α对。

也就是说，b是a的α倍（模p）。有了这个概念，就可以进行一项"系数知识测试"：

• Bob秘密选一个随机的α值，生成一个α对：$(a,b)=(a,\alpha \cdot a)$

• Bob把这个α对$(a,b)$发送给Alice

• Alice需要回复一个不同的α对：$(a^{\prime },b^{\prime })$

• Bob验证$(a^{\prime },b^{\prime })$是不是一个α对，如果是则接受该回复

乍一看有点迷糊，既然$b=\alpha \cdot a$，那Alice不就是可以反推出α等于多少了吗？请注意：这里的乘法是模p乘法。举个例子就清楚了：

假设Bob选定$a=2,\alpha =4$，那么$b=\alpha \cdot a=4\cdot 2{|}_{mod7}=1$，所以最终生成的α对是$(2,1)$，Alice没法反推出α的值是多少（在p非常大的情况下，这是一个离散对数难题）。

既然Alice不知道α，那么她就只有一种方法可以生成新的α对：给a和b各乘上同一个系数$\gamma$。

举个例子，假设Alice秘密选定$\gamma =5$，那么新生成的α对：

$(a^{\prime },b^{\prime })=(\gamma \cdot a,\gamma \cdot b)=(5\cdot 2{|}_{mod7},5\cdot 1{|}_{mod7})=(3,5)$

Bob收到这个新的α对$(a^{\prime },b^{\prime })$之后，验证$\alpha \cdot a^{\prime }=4\cdot 3{|}_{mod7}=12{|}_{mod7}=5=b^{\prime }$，接受该回复。

也就是说，Alice秘密持有$\gamma$，Bob秘密持有$\alpha$。跟上一篇文章中的图拼到一起：

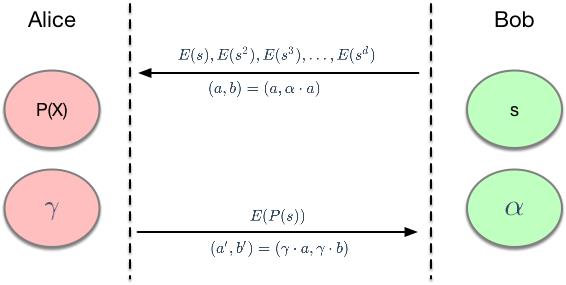
这就是所谓的"系数知识假设"，英文是"Knowledge of Coefficient Assumption"，简称KCA。一句话概括：所谓KCA，指的是如果Alice成功回复了一个α对，那么她一定持有某个$\gamma$使得$a^{\prime }=\gamma \cdot a$。

更多文章欢迎关注“鑫鑫点灯”专栏：https://blog.csdn.net/turkeycock
或关注飞久微信公众号：