卡通驱动项目ThreeDPoseTracker——关键点平滑方案解析

Posted 2022-11-22 风翼冰舟

前言

之前对ThreeDPoseTracker的深度学习模型和unity中的驱动方法进行过解析，还有一个比较重要的就是从深度学习模型出来的3D关键点数据会有抖动，在ThreeDPoseTracker源码中有做两次平滑，一部分是卡尔曼滤波，还有一部分是低通滤波。这次就是对这部分类型进行解析。

国际惯例参考博客：

ThreeDPoseTracker源码VNectBarracudaRunner.cs

理论与代码复现

在源工程的VNectBarracudaRunner.cs脚本中，有一个函数KalmanUpdate便是用于卡尔曼滤波的，而后续有这样一行代码：

jp.PrevPos3D[i] = jp.PrevPos3D[i] * Smooth + jp.PrevPos3D[i - 1] * (1f - Smooth);

便是低通滤波器。

卡尔曼滤波

其实这部分和我在网上搜到的卡尔曼滤波的方法公式很不相同，不过我们还是按照源码来实现解析吧，因为卡尔曼滤波的真正理论貌似有点复杂，暂时不准备去看。

在源码中，预定义了两个参数：KalmanParamQ、KalmanParamR，为了简写公式就简记为Q和R，随后按照时间推移不断迭代求解两个数组K和P，公式如下：
$$\begin{array}{rl}K& =\frac{P+Q}{P+Q+R}\\ P& =R\times \frac{P+Q}{P+R+Q}\end{array}$$
随后使用K对关键点进行平滑，首先得有一个中间变量X，设未平滑的姿态为C，则平滑后的姿态D:
$$\begin{array}{rl}D& =X+(C-X)\ast K\\ X& =D\end{array}$$
这就没了，感觉跟网上的卡尔曼滤波理论完全不同，如果有哪位大佬知道这个究竟属于什么算法，可以在评论区告知或者微信公众号私信讨论，谢谢。

低通滤波

这个和图像里面的低通滤波差不多，不过是一维的，公式很简单
$$now=prev\ast smooth+now\ast (1-smooth)$$
简单的写法是上面，论文用了一个时间轴，将历史的6帧数据联合起来为当前帧平滑，代码如下

jp.PrevPos3D[0] = jp.Pos3D;
for (var i = 1; i < NOrderLPF; i++)

    jp.PrevPos3D[i] = jp.PrevPos3D[i] * Smooth + jp.PrevPos3D[i - 1] * (1f - Smooth);

jp.Pos3D = jp.PrevPos3D[NOrderLPF - 1];

历史第0帧为当前未平滑的帧数据，然后依次向前平滑到帧窗口的最后一帧，那么当前帧平滑后的数据就是窗口的最后一帧。

实验

原始、unity平滑结果、python卡尔曼滤波、python卡尔曼+低通滤波三种方法平滑后的脚部z轴方向的坐标变化如下：

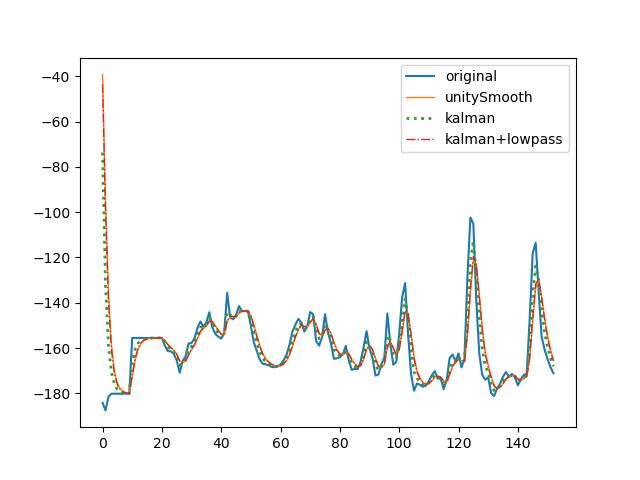
很清晰发现原始数据有很多小棱角的噪声，而经过kalman滤波以后，基本去掉了大部分棱角，然后用低通滤波降低了运动幅度。最终结果与unity源码结果相同，说明复现成功。

我们来看看动作的可视化效果：

未经平滑的可视化

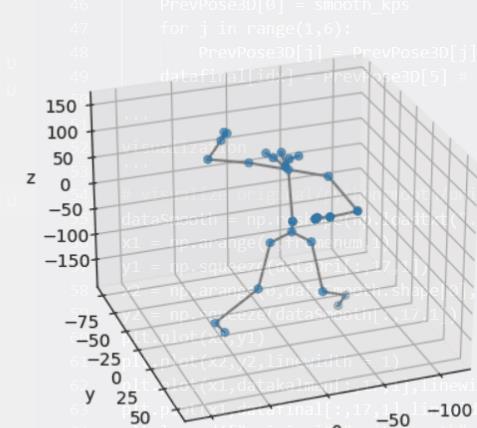
经过卡尔曼和低通平滑后：

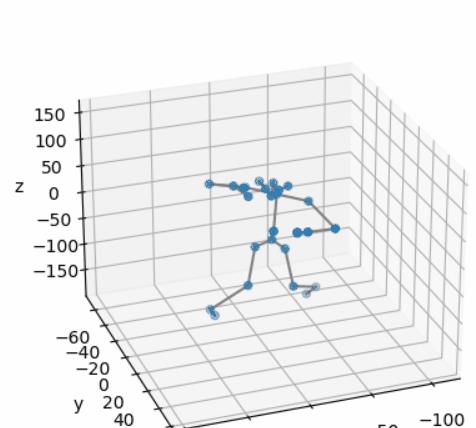
结论

论文的平滑方法虽然很少代码就搞定，但是从效果图可以发现，平滑效果还是不错的。

完整的python实现放在微信公众号的简介中描述的github中，有兴趣可以去找找。或者在公众号回复“ThreeDPose"，同时文章也同步到微信公众号中，有疑问或者兴趣欢迎公众号私信。