2d Laser 和 Odomter 内外参数标定工具原理及使用方法
Posted 白巧克力亦唯心
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了2d Laser 和 Odomter 内外参数标定工具原理及使用方法相关的知识,希望对你有一定的参考价值。
前言
两轮差速轮式机器人可以基于码盘数据和两轮间距以及车轮半径进行航迹推演,得到机器人的轨迹。激光雷达也可以利用 icp 等算法计算出两时刻间机器人的相对运动量。因此,可以利用两者数据进行融合定位,本博客根据 Censi 2013 年发表在 TRO 上的论文 《Simultaneous calibration of odometry and sensor parameters for mobile robots》,对如何标定里程计内参数 ( 轮子半径,两轮间距),以及外参数(激光和里程计之间的坐标关系)进行理论推导,并将对应标定代码整理在了我们的网站上。
说明: 这里的标定仅仅是 3 自由度的(激光坐标系和机器人坐标系都是平行于地面的,只能标定 yaw 和xy),如果还想标定激光相对于水平面的(pitch,roll,主要是安装误差,激光安装的并不水平),可以参考如下两篇论文:
- 2007 年 bmvc, Fully Automated Laser Range Calibration
- 2016 年 TRO, Full-DOF Calibration of a Rotating 2-D LIDAR with a Simple Plane Measurement
标定原理
原理概述
如下图所示,由于机器人在平面上运动,机器人相对于固定坐标系的姿态可以用 SE(2) 表示 q = ( q x , q y , q θ ) ∈ S E ( 2 ) \\boldsymbolq=\\left(q_x, q_y, q_\\theta\\right) \\in \\mathrmSE(2) q=(qx,qy,qθ)∈SE(2). 考虑到水平上运动,2d 激光通过自身无法确定 roll 和 pitch , 也无法知道相对于地面的高度,因此假设机器人运动时,激光坐标系在一个平行于地面的平面上运动,激光坐标系 (sensor frame) 坐标系相对于机器人坐标系的姿态为 ℓ = ( ℓ x , ℓ y , ℓ θ ) ∈ SE ( 2 ) \\boldsymbol\\ell=\\left(\\ell_x, \\ell_y, \\ell_\\theta\\right) \\in \\operatornameSE(2) ℓ=(ℓx,ℓy,ℓθ)∈SE(2).
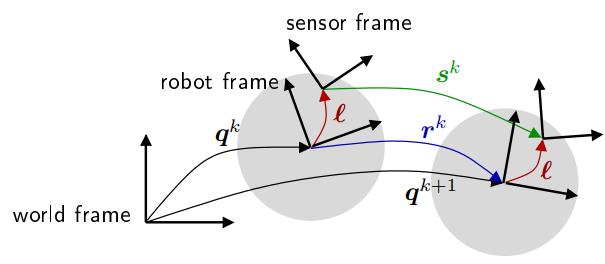
通常机器人两个轮子上各自装有一个编码器,能够计算左右轮的速度
ω
L
,
ω
R
\\omega_\\mathrmL, \\omega_\\mathrmR
ωL,ωR,利用左右轮速度以及轮半径和轮间距能够计算移动机器人前进速度
v
v
v 和旋转角速度
ω
\\omega
ω
(
v
ω
)
=
J
(
ω
L
ω
R
)
\\left( \\beginarraylv \\\\ \\omega\\endarray\\right)=\\boldsymbolJ \\left( \\beginarrayc\\omega_\\mathrmL \\\\ \\omega_\\mathrmR\\endarray\\right)
(vω)=J(ωLωR)
其中
J
\\boldsymbolJ
J 是一个关于左右轮半径及轮间距
r
L
,
r
R
,
b
r_\\mathrmL, r_\\mathrmR, b
rL,rR,b 的函数:
J
=
(
J
11
J
12
J
21
J
22
)
=
(
+
r
L
/
2
+
r
R
/
2
−
r
L
/
b
+
r
R
/
b
)
\\boldsymbolJ=\\left( \\beginarrayllJ_11 & J_12 \\\\ J_21 & J_22\\endarray\\right)=\\left( \\beginarraycc+r_\\mathrmL / 2 & +r_\\mathrmR / 2 \\\\ -r_\\mathrmL / b & +r_\\mathrmR / b\\endarray\\right)
J=(J11J21J12J22)=(+rL/2−rL/b+rR/2+rR/b)
当得到机器人前进速度和旋转速度以后,进行积分,就能得到车体姿态
q
\\boldsymbolq
q. 具体推导过程可参看我之前的博客。
考虑一段时间
t
∈
[
t
k
,
t
k
+
1
]
t \\in\\left[t_k, t_k+1\\right]
t∈[tk,tk+1],里程计推算得到的两个时刻机器人坐标系的姿态
q
k
\\boldsymbolq^k
qk 和
q
k
+
1
\\boldsymbolq^k+1
qk+1,利用外参数
ℓ
\\boldsymbol\\ell
ℓ 可以得到两时刻时间激光坐标系的相对变化量
s
k
=
⊖
(
q
k
⊕
ℓ
)
⊕
(
q
k
+
1
⊕
ℓ
)
(
1
)
\\boldsymbols^k=\\ominus\\left(\\boldsymbolq^k \\oplus \\boldsymbol\\ell\\right) \\oplus\\left(\\boldsymbolq^k+1 \\oplus \\boldsymbol\\ell\\right) ~~~~~~~ (1)
sk=⊖(qk⊕ℓ)⊕(qk+1⊕ℓ) (1)
其中
⊕
\\oplus
⊕ 表示 SE(2) 加法:
(
a
x
a
y
a
θ
)
⊕
(
b
x
b
y
b
θ
)
=
(
a
x
+
b
x
cos
(
a
θ
)
−
b
y
sin
(
a
θ
)
a
y
+
b
x
sin
(
a
θ
)
+
b
y
cos
(
a
θ
)
a
θ
+
b
θ
)
\\left( \\beginarrayla_x \\\\ a_y \\\\ a_\\theta\\endarray\\right) \\oplus \\left( \\beginarraylb_x \\\\ b_y \\\\ b_\\theta\\endarray\\right)=\\left( \\beginarrayca_x+b_x \\cos \\left(a_\\theta\\right)-b_y \\sin \\left(a_\\theta\\right) \\\\ a_y+b_x \\sin \\left(a_\\theta\\right)+b_y \\cos \\left(a_\\theta\\right) \\\\ a_\\theta+b_\\theta\\endarray\\right)
⎝⎛axayaθ⎠⎞⊕⎝⎛bxbybθ⎠⎞=⎝⎛ax+bxcos(aθ)−bysin(aθ)a