杠上数据结构 - 二叉树
Posted 星火燎原2016
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了杠上数据结构 - 二叉树相关的知识,希望对你有一定的参考价值。
二叉树在面试过程中出现的频率非常高,因此熟练掌握二叉树是吊打面试官的必备技能。
基本认识
二叉树:是节点的一个有限集合,该集合要么为空,要么由一个根节点加上左子树和右子树组成。
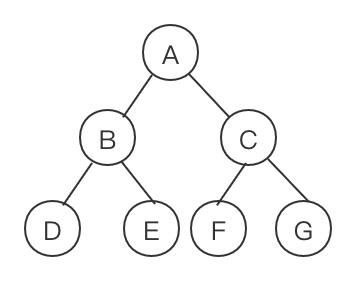
特点:
- 每个节点最多有两颗子树,即二叉树不存在度大于 2 的节点。
- 二叉树的子树有左右之分,左子树在左,右子树在右。
二叉树的存储结构
二叉树的存储结构有:
- 顺序存储
- 链式存储
顺序存储
顺序存储是使用一维数组存储二叉树中的节点,节点的存储位置就是数组的下表索引。
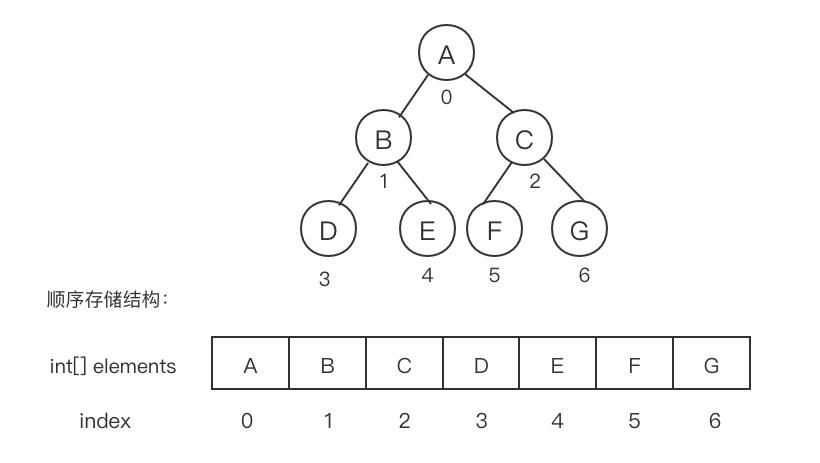
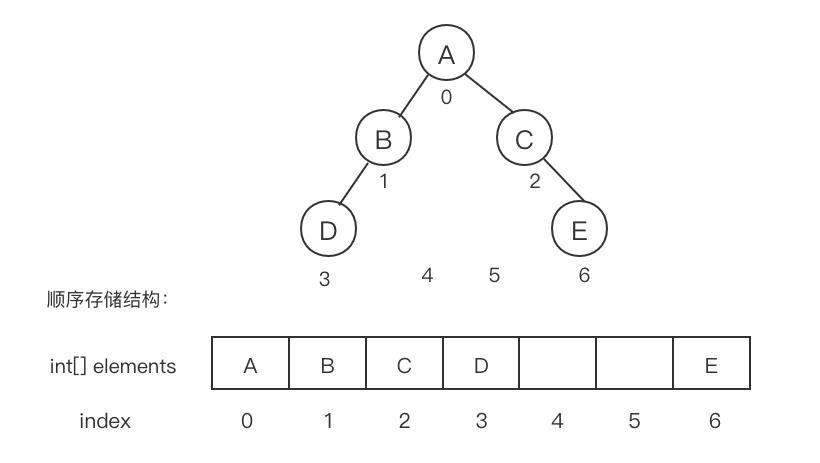
可以看到,顺序存储结构在存储非完全二叉树时,会出现空间利用不完全的问题。对于某种极端情况,比如只有左子树,或只有右子树,采用顺序存储结构是十分浪费空间的。因此顺序存储一般适用于完全二叉树。
链式存储
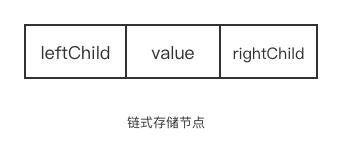
链式存储是使用链表来存储,每个节点包含三个域: 数据域和左右孩子域。
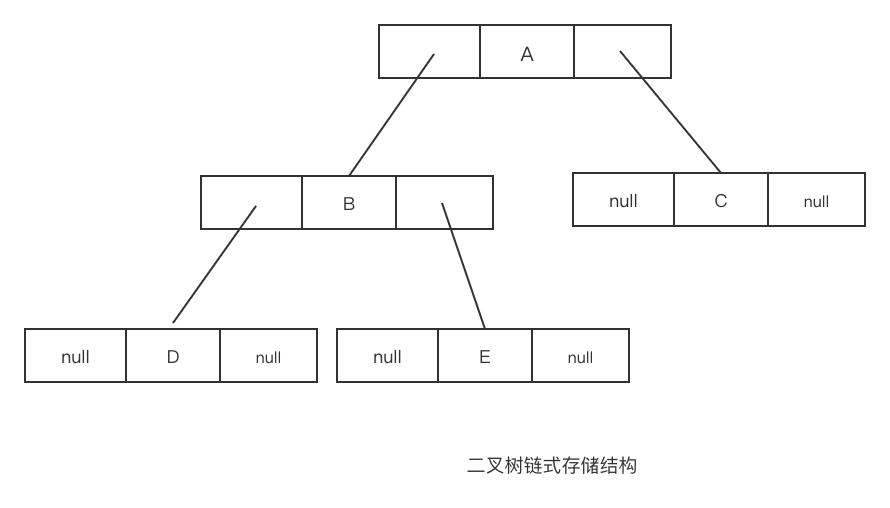
二叉树遍历
二叉树的遍历方式有:
- 先序遍历
- 中序遍历
- 后序遍历
- 层级遍历
其中先中后序都是相对于根节点而言的,先序就是先根再左右孩子,中序就是先左孩子再根最后右孩子,后续就是先左孩子再右孩子最后根。层级遍历就是从上往下一层层的访问节点。
例如上面二叉树链式存储结构图,
先序: A B D E C
中序: D B E A C
后续: D E B C A
层级: A B C D E
二叉树遍历代码实现
定义二叉树节点类:
/**
* 二叉树的节点
*/
public class Node
private int value;
private Node left;
private Node right;
public Node()
public Node(int value)
this.value = value;
public int getValue()
return value;
public void setValue(int value)
this.value = value;
public Node getLeft()
return left;
public void setLeft(Node left)
this.left = left;
public Node getRight()
return right;
public void setRight(Node right)
this.right = right;
@Override
public String toString()
return "ListNode" +
"value=" + value +
", left=" + left +
", right=" + right +
'';
定义二叉树类, 通过根节点来定义:
/**
* 二叉树类
*/
public class BinaryTree
/**
* 根节点
*/
private Node root;
public BinaryTree()
public BinaryTree(int value)
Node node = new Node(value);
setRoot(node);
public Node getRoot()
return root;
public void setRoot(Node root)
this.root = root;
1. 插入节点
/**
* 往二叉树中插入节点
*
* @param value
*/
public void add(int value)
Node newNode = new Node(value);
// 没有根节点时,插入到根节点
if (root == null)
root = newNode;
else // 有节点
Node curNode = root;
while (true)
// 插入节点的值小于当前节点的值,放到当前节点的左边
if (value < curNode.getValue())
// 如果当前节点没有左孩子,则直接放入,否则继续循环
if (curNode.getLeft() == null)
curNode.setLeft(newNode);
break;
curNode = curNode.getLeft();
else if (value > curNode.getValue()) // 插入节点大于当前节点的值,放到节点的右边
if (curNode.getRight() == null)
curNode.setRight(newNode);
break;
curNode = curNode.getRight();
2. 先序遍历
/**
* 先序遍历,输出到 List 集合中
*
* @return
*/
private void pre2(Node node, List<Integer> list)
if (node == null)
return;
list.add(node.getValue());
pre2(node.getLeft(), list);
pre2(node.getRight(), list);
3. 中序遍历
/**
* 中序遍历
*
* @param node
* @param list
*/
private void middle(Node node, List<Integer> list)
if (node == null || list == null)
return;
middle(node.getLeft(), list);
list.add(node.getValue());
middle(node.getRight(), list);
4. 后序遍历
/**
* 后续遍历
*
* @param node
* @param list
*/
private void after(Node node, List<Integer> list)
if (node == null || list == null)
return;
after(node.getLeft(), list);
after(node.getRight(), list);
list.add(node.getValue());
5. 层级遍历
/**
* 层级遍历(最基本的): 通过队列来实现
*/
public List<Integer> levelTraversal()
List<Integer> list = new ArrayList<>();
if (root == null)
return list;
Queue<Node> queue = new LinkedList<>(); // 定义一个队列
queue.add(root); // 根节点先插入队列
Node curNode;
while (!queue.isEmpty()) // 队列不为空,循环取出元素
curNode = queue.poll();
list.add(curNode.getValue());
if (curNode.getLeft() != null)
queue.add(curNode.getLeft());
if (curNode.getRight() != null)
queue.add(curNode.getRight());
return list;
6. 层级遍历, 并把每层分成一组
/**
* 层级遍历,将每一层分成一个单独的组
*/
public List<List<Integer>> levelTraversalGroup()
List<List<Integer>> resultList = new ArrayList<>(); // 包含每层的外部 list
if (root == null)
return resultList;
Queue<Node> queue = new LinkedList<>();
queue.offer(root);
while (!queue.isEmpty())
List<Integer> sublist = new ArrayList<>(); // 存放每一层中的元素 list
int size = queue.size(); // 此时的 size() 大小就是每层中元素的个数
for (int i = 0; i < size; i++)
Node curNode = queue.poll();
sublist.add(curNode.getValue());
if (curNode.getLeft() != null)
queue.offer(curNode.getLeft());
if (curNode.getRight() != null)
queue.offer(curNode.getRight());
resultList.add(sublist); // 将每层的list 加入到外部 list 中
return resultList;
7. 层级遍历, 把每层分成一组, 并按照奇数层从右往左,偶数层从左往右
/**
* 层级遍历,将每一层分为单独的一组,并且按照 z 字形输出
*
* @return
*/
public List<List<Integer>> levelTraversalGroupZ()
List<List<Integer>> resultList = new ArrayList<>(); // 包含每层的外部 list
if (root == null)
return resultList;
Queue<Node> queue = new LinkedList<>(); // LinkedList 实现队列
queue.offer(root);
boolean right2Left = true;
while (!queue.isEmpty())
List<Integer> sublist = new ArrayList<>(); // 存放每一层中的元素 list
int size = queue.size(); // 此时的 size() 大小就是每层中元素的个数
for (int i = 0; i < size; i++)
Node curNode = queue.poll();
if (right2Left)
sublist.add(0, curNode.getValue());
else
sublist.add(curNode.getValue());
if (curNode.getLeft() != null)
queue.offer(curNode.getLeft());
if (curNode.getRight() != null)
queue.offer(curNode.getRight());
right2Left = !right2Left;
resultList.add(sublist); // 将每层的list 加入到外部 list 中
return resultList;
8. 深度优先遍历
/**
* 二叉树深度遍历,利用堆栈,先将右子树压栈,再将左子树压栈,这样左子树就再栈顶。
*
* @return
*/
private List<Integer> depthTraversal(Node root)
List<Integer> list = new ArrayList<>();
if (root == null)
return list;
Stack<Node> stack = new Stack<>();
stack.push(root);
while (!stack.isEmpty())
Node node = stack.pop();
list.add(node.getValue());
if (node.getRight() != null)
stack.push(node.getRight());
if (node.getLeft() != null)
stack.push(node.getLeft());
return list;
9. 获取第 k 层节点
/**
* 获取第 k 层元素
*
* @param level
* @return
*/
public List<Integer> getDataByLevel(int level)
List<Integer> list = new ArrayList<>();
if (root == null || level < 1)
return list;
Queue<Node> queue = new LinkedList<>();
queue.offer(root);
int curLevel = 1;
while (!queue.isEmpty())
int size = queue.size(); // 此时的 size() 大小就是每层中元素的个数
for (int i = 0; i < size; i++)
Node curNode = queue.poll();
if (level == curLevel)
list.add(curNode.getValue());
if (curNode.getLeft() != null)
queue.offer(curNode.getLeft());
if (curNode.getRight() != null)
queue.offer(curNode.getRight());
curLevel++;
return list;
10. 查找某个值
/**
* 查找某个值
*/
private boolean query(Node node, int value)
if (node == null)
return false;
if (value < node.getValue())
return query(node.getLeft(), value);
else if (value > node.getValue())
return query(node.getRight(), value);
else
return true;
10. 获取二叉树的深度
private int getTreeDepth(Node node)
if (node == null)
return 0;
int left = getTreeDepth(node.getLeft());
int right = getTreeDepth(node.getRight());
return left > right ? left + 1 : right + 1;
11. 判断二叉树是否是平衡二叉树
private boolean isBalanceTree(Node node)
if (node == null)
return true;
int lh = getTreeDepth(node.getLeft());
int rh = getTreeDepth(node.getRight());
return Math.abs(lh - rh) <= 1 && isBalanceTree(node.getLeft()) && isBalanceTree(node.getRight());
测试代码
public class BinaryTreeDemo
public static void main(String[] args)
// 构建一个二叉树
/**
* 6
* / \\
* 4 9
* / \\ / \\
* 2 5 7 10
* / \\
* 1 3
* /
* 0
*
*
*/
BinaryTree binaryTree = new BinaryTree();
int[] arr <以上是关于杠上数据结构 - 二叉树的主要内容,如果未能解决你的问题,请参考以下文章