数字图像处理——基本运算

Posted 2022-11-13 _瞳孔

一：一些概念

1.1：相邻像素

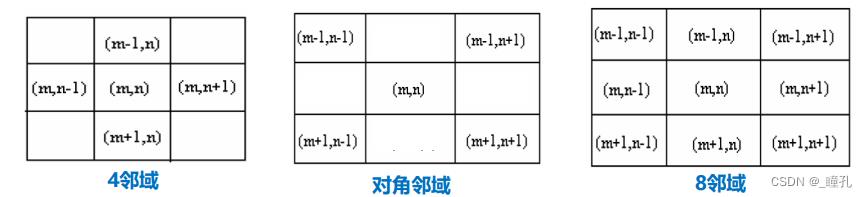
相邻像素(对于像素p(m,n))

• 4邻域：N₄(p)
• 对角邻域：N_D(p)
• 8邻域：N₈(8)

像素邻接：像素的相邻仅说明了两个像素在位置上的关系，若再加上取值相同或相近，则称两个像素邻接

1.2：像素距离

距离的度量：对于像素点 p(x,y), q(s,t), z，如果度量D满足以下条件，则称为距离的度量函数

• 正定性： 𝐷(𝑝, 𝑞) ≥ 0; (𝑖𝑓 𝑝 = 𝑞, 𝐷(𝑝, 𝑞) = 0)
• 对称性： 𝐷(𝑝, 𝑞) = 𝐷(𝑞, 𝑝)
• 距离三角不等式： 𝐷(𝑝, 𝑞) ≤ 𝐷(𝑝, 𝑧) + 𝐷(𝑧, 𝑞)

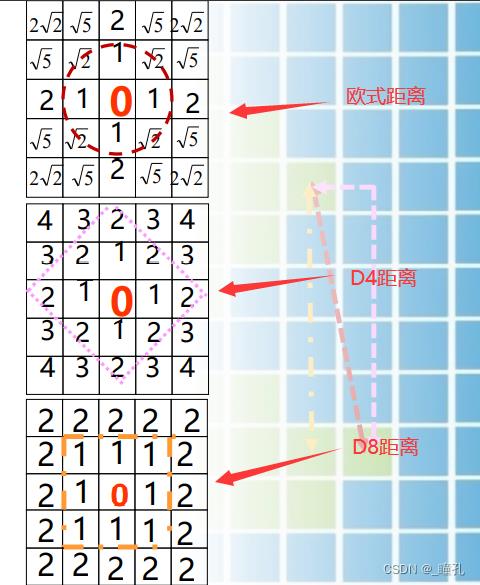
三种常见距离：

• 欧式距离 (像素点 p(x,y), q(s,t)) : 𝐷𝑒(𝑝, 𝑞) = sqrt((𝑥 − 𝑠)²+(𝑦 − 𝑡)²)
• D4距离（街区距离）：𝐷₄(𝑝, 𝑞) = |𝑥 − 𝑠| + |𝑦 − 𝑡|
• D8距离（棋盘格距离）：𝐷₈(𝑝, 𝑞) = max(|𝑥 − 𝑠| , |𝑦 − 𝑡|)

二：算数运算

算术运算是指对两幅或多幅输入图像进行点对点的加、减、乘、除计算而得到输出图像的运算

• 对应空间位置的像素间运算，element-wise / pixel-wise
• 在相同大小的图像间进行

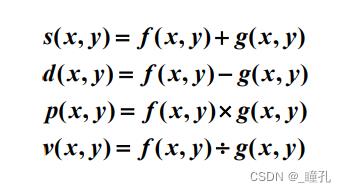
2.1：图像加法

图像加法，以加权融合为例：

• l_1 + l_2 = S_1
• 0.6 * l_1 + 0.4 * l_2 = S_2

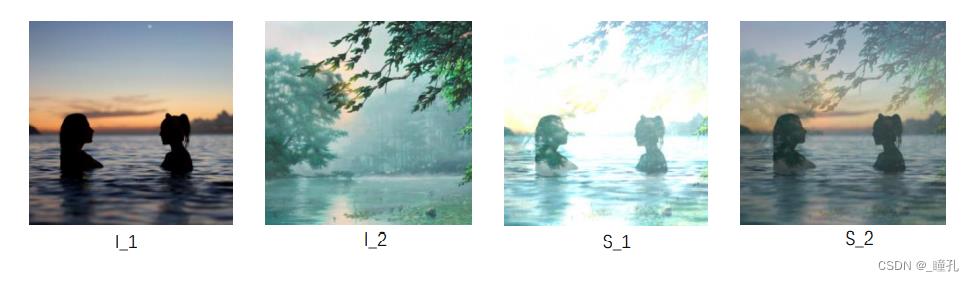
2.2：图像减法

图像减法，以一阶导数为例，图像的一阶和二阶导数：不连续函数f(x,y)的导数, 严格来说不算能算作导数, 只是形式上与真正的导数相似. 取Δx=1, 一阶与二阶偏导数分别为:

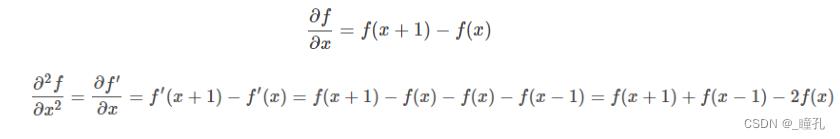
图像加、减法，以图像锐化为例：

• H = X – blur(X)
• Y = X +ɑH

2.3：图像乘法

图像乘法：对应像素相乘，常用于Mask、Attention等操作

2.4：算术运算应用示例

低照度图像增强（Low Light Image Enhancement）

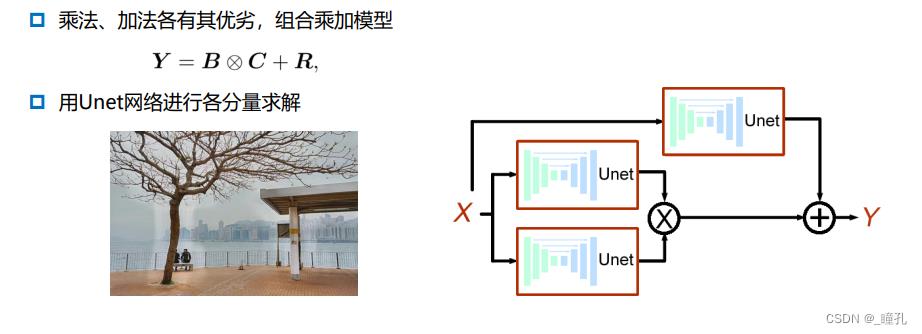
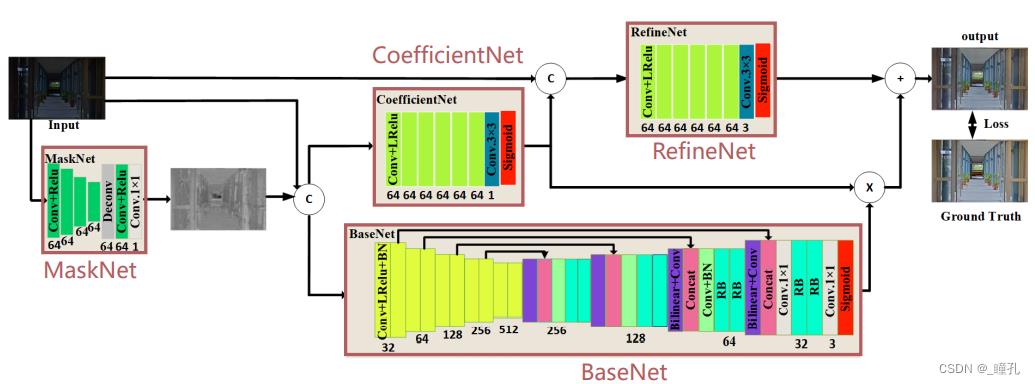
三：直方图运算

图像直方图（Image Histogram）：描述图像的各个灰度级的统计特性，它是图像灰度值的函数，统计图像中各个灰度级出现的次数或频率。其横坐标为图像中各个像素点的灰度级别，纵坐标表示具有各个灰度级别的像素在图像中出现的次数和频率。

直方图运算计算代价较小，且具有图像平移、旋转、缩放不变性等众多优点，广泛地应用于图像处理的各个领域，特别是灰度图像的阈值分割、基于颜色的图像检索以及图像分类。

3.1：灰度直方图

直方图是图像的一种统计表达 ，直方图反映了图像中灰度的分布情况。

直方图并不反映图像的空间信息，只展示具有一定灰度级的像素的数目或频数，通过对图像的直方图进行改变可以改善图像的质量

设图像中某种灰度r_k的像素数为n_k，n是图像中像素的总数，则灰度级r_k所对应的频数为：

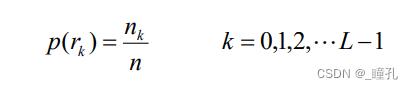
四类图像的直方图特征：

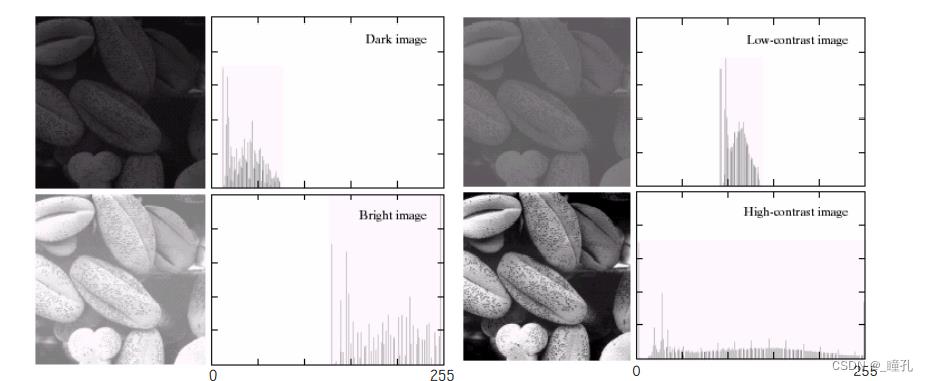
3.2：直方图均衡化

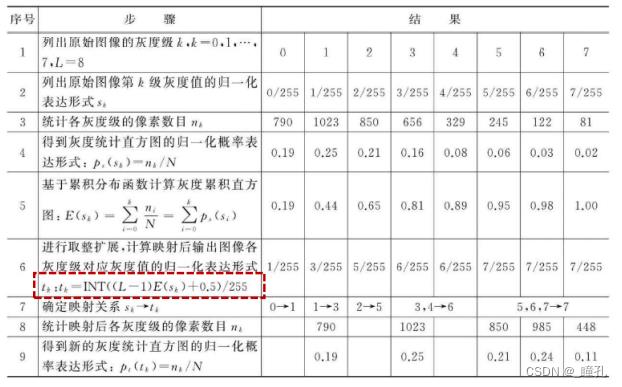
直方图均衡化（Histogram Equalization）通过某种灰度映射（如非线性拉伸）使原始图像的直方图变换为在整个灰度范围内均匀分布，即灰度的概率密度分布变为常数。可以增加像素灰度值的动态范围，增强图像整体对比度。

累积分布函数CDF可以把r变换到均衡化s，证明如下：

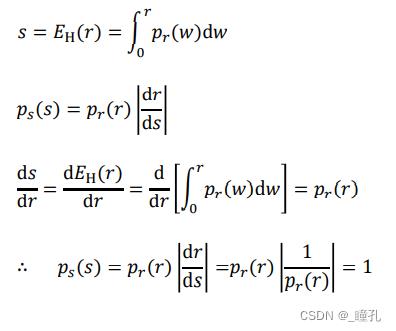
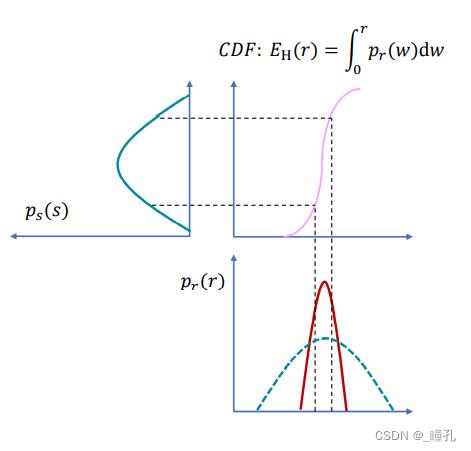
离散情况：累积直方图

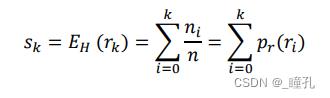
说明：

• 𝑠_𝑘是 k 的单值单增函数
• 灰度取值范围一致，0 ≤ 𝑠_𝑘 ≤ 1
• 将r的分布转换为s 的均匀分布

均衡化的缺点

• 增强效果不易控制，处理的结果总是得到全局均匀化的直方图。
• 均衡化图像的动态范围扩大，本质上是扩大了量化间隔，但量化级别（灰度级）反而减少了，导致某些图像细节消失。
• 对于直方图存在高峰的图像，经处理后对比度可能过分增强。
• 原来灰度值不同的像素经过处理后可能变为相同，从而形成一片灰度值相同的区域，各区域之间有明显的边界，导致出现伪轮廓。

3.3：直方图规定化

直方图规定化(Histogram Matching)：也常叫直方图匹配，指变换图像灰度直方图为指定的分布，从而有选择地增强某个灰度范围内的对比度

• 比均衡化更灵活，可以指定目标分布
• 能有效地改善图像的整体或局部特征，广泛运用在图像增强处理中
• 保证不同图像的影调风格的一致性，在处理艺术图像时十分有用

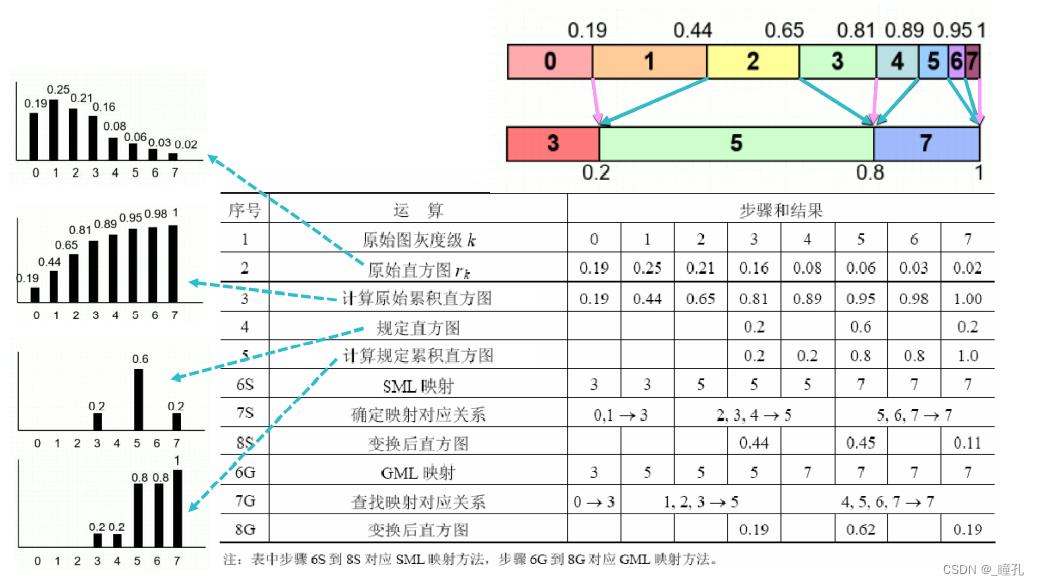
直方图规定化的步骤，借助直方图均衡变换实现规定的灰度映射：

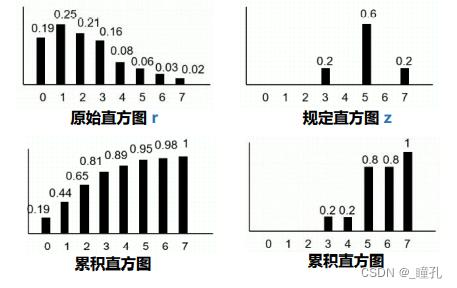
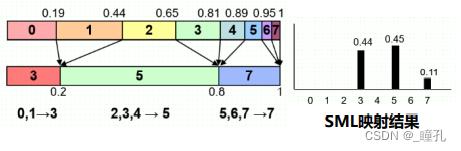
单映射规则SML (Single Mapping Law)：依次找到灰度级映射后的单个灰度级，逐个对应。比较直观，但可能产生较大的取整误差。

组映射规则GML (Group Mapping Law)：寻找最接近的对应灰度，中间的灰度级看作一组。映射误差用对应映射间数值的差值的绝对值的和来度量。

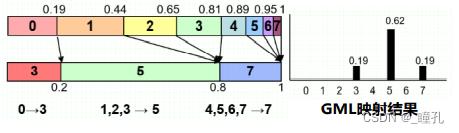
GML映射规则产生的误差小于SML。

SML: |0.44-0.2|+ |0.45-0.6|+|0.11-0.2|=0.48
GML: |0.19-0.2|+ |0.62-0.6|+|0.19-0.2|=0.04

3.4：直方图运算应用示例

神经风格迁移

• Image Style Transfer Using Convolutional Neural Networks(使用卷积神经网络的图像风格转换)
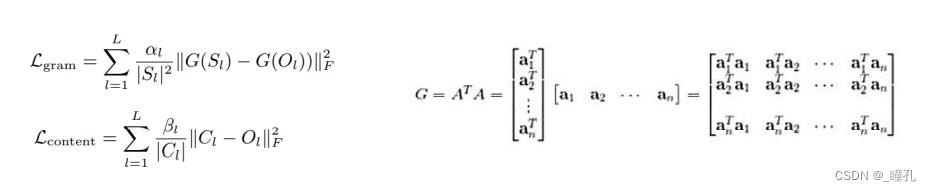
  • Gatys 2015: S和O是VGG网络特定层输出的特征；G为计算Gram Matrix
  • 输入噪声，用两个loss的梯度来迭代更新生成图像；Gram矩阵会扩大原本值的差异，突出风格和特点，但是Gram矩阵并非完美，会引起瑕疵。

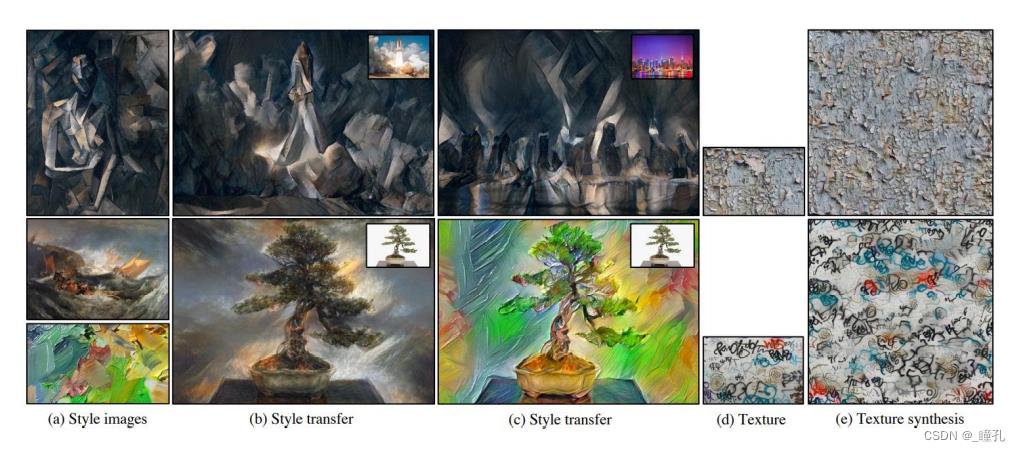
基于直方图匹配的神经风格迁移：

• Stable and Controllable Neural Texture Synthesis and Style Transfer Using Histogram Losses, 2017(使用直方图损失进行稳定可控的神经纹理合成和风格转换)

• Stable and Controllable Neural Texture Synthesis and Style Transfer Using Histogram Losses, 2017
  • 使用常规 histogram matching technique 来匹配源纹理图的直方图
  • 直方图匹配loss： O还是VGG输出特征，R为按风格S的直方图匹配操作

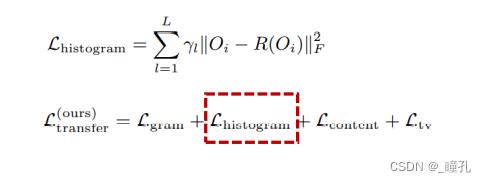
如果有兴趣了解更多相关内容，欢迎来我的个人网站看看：瞳孔空间