数据结构：图解归并过程

Posted 2022-11-10 流楚丶格念

文章目录

• 先来个传统的归并排序，也是咱们学的多的
• • 算法图解
  • 代码实现
  • 时间复杂度
• 接下来是一些奇怪的名词就冒出来了
• • 二路归并
  • 多路归并（三路为例）：
  • 归并趟数

先来个传统的归并排序，也是咱们学的多的

算法图解

我们首先来详细说说归并排序的算法思路，归并排序的算法思路并不复杂，其主要是一个拆分与合并的过程，接下来我们用图解来看看归并排序究竟是如何排序的。

首先，我们得到了这样的一个数组：

之后我们将其进行一次按照中间位置一分为二的划分：

之后我们在此基础上再为这两个被划分出来的数组进行进一步划分：

只要每个数组长度大于1，那么我们就会继续划分，因此在上图中的情况下我们仍然要继续划分，如图所示：

被划分成这个状态之后，我们便不再划分，而是两两将其进行有序数组的拼接，如图所示：

在此拼接的基础上我们继续拼接，只要这个数组还是被划分为多个子数组的状态我们就会一直继续拼接，下次拼接的结果如图所示：

我们继续拼接，如下图，发现整个数组又变成一个了，拼接完成：

现在我们可以总结出归并排序的算法思路了，那就是在将整个数组进行不断划分，知道划分的每个字数组的长度为0或者为1，这是每个字数组统统都是有序数组，这是再按照有序数组的拼接算法，对每个子数组进行拼接，这样就能保证每次的拼接结果都还是有序的最终拼接成一个之后，整个数组便都是有序的，而数组的排序也宣布完成，关于这个字数组的划分，实际上是通过递归实现的逻辑上的划分

代码实现

在我们了解了归并排序的基本算法之后，就要开始着手实现这个排序了。

递归分治：

在上面的排序算法图解中，并没有着重的介绍有序数组的合并是如何实现的，因此在之后的总结中，我还会介绍如何进行合并，不过首先我们来看看对于这个排序中的拆分过程时候如何使用代码实现的：

/**
 * 分治
 * @param arr
 * @param left
 * @param right
 */
private static void mergeSort(int[] arr, int left, int right) 
    if (left >= right) 
        return;
    
    int mid = (left + right) / 2;
    // 分治左边
    mergeSort(arr, left, mid);
    // 分治右边
    mergeSort(arr, mid + 1, right);
    // 归并左边右边
    ...

代码解析：

对于拆分过程实际上就是递归，我们不断进行左右的递归，并不断减小子数组的规模，最终便会减小到每个数组的规模为1或者为0

这里需要注意的是递归出口的判断条件为：left>=right，我们为什么不写成left==right呢？

这是因为在右递归中，我们的左边界为mid+1，我们的mid是通过直接整除2得到的，当数组规模为1的时候，mid的运算结果为0，此时进入下一层递归时，左递归的左右边界都是0，下层左递归正常退出，但是右递归这是便出现了问题，这是右递归中的right = mid + 1，为1，如果使用left==right，就无法判断并终止这个情况了，所有此时我们还要加入一个新情况，那就是left>right，所以我们合写为left>=right。

合并：

之后我们来探讨合并的过程，在合并的时候我们需要使用到一个额外空间，在合并时，我们需要先将合并结果存放在那个额外的新空间上，然后再将新空间上的结果复制回我们的当前数组位置上

例如：在数组1,3,0,6的分组合并过程中，1，3和0，6分别被分进了不同的组中，我们为两组分别声明i指针和j指针，同时为临时空间声明n指针，我们每次对两个数组中的指针指向数字进行比较，小的会被移动到额外的临时空间中，同时那个数组中的指针要向前移动一步，之后我们继续比较。最终我们会得到一个有序的数组，但是这个数组是被存放在临时空间中的，因此我们需要将它再复制回原数组中

接下来我们看代码实现：

/**
 * 归并
 * @param arr
 * @param left
 * @param mid
 * @param right
 */
private static void merge(int[] arr, int left, int mid, int right) 
    // 拿到左半部分首元素下标
    int s1 = left;
    // 拿到右半部分首元素下标
    int s2 = mid + 1;
    // 临时数组：计算，存储归并后的数组，最后再进行赋值
    int[] temp = new int[right - left + 1];
    // 临时数组当前访问到的下标
    int index = 0;
    while (s1 <= mid && s2 <= right) 
        // 如果第一个数组的指针数值小于第二个数组的，那么其放置在临时空间上
        if (arr[s1] <= arr[s2]) 
            temp[index++] = arr[s1++];
         else     // 否则是第二个数组的数值放置于其上
            temp[index++] = arr[s2++];
        
    
    // 如果这是s1仍然没有到达其终点，那么说明它还有剩下，直接接上就好
    while (s1 <= mid) 
        temp[index++] = arr[s1++];
    
    while (s2 <= right) 
        temp[index++] = arr[s2++];
    
    // 数组复制
    for (int i = 0; i < temp.length; i++) 
        arr[i + left] = temp[i];
    

完整代码如下：

package com.yyl.algorithm.mergesort;

import java.util.Arrays;

public class MergeSort 
    public static void main(String[] args) 
        int[] arr = new int[]5, 7, 4, 2, 0, 3, 1, 6;
        // int[] arr = new int[]1,0;
        int left = 0;
        int right = arr.length - 1;
        mergeSort(arr, left, right);
        System.out.println(Arrays.toString(arr));
    

    /**
     * 分治
     * @param arr
     * @param left
     * @param right
     */
    private static void mergeSort(int[] arr, int left, int right) 
        if (left >= right) 
            return;
        
        int mid = (left + right) / 2;
        // 分治左边
        mergeSort(arr, left, mid);
        // 分治右边
        mergeSort(arr, mid + 1, right);
        // 归并左边右边
        merge(arr, left, mid, right);
    

    /**
     * 归并
     * @param arr
     * @param left
     * @param mid
     * @param right
     */
    private static void merge(int[] arr, int left, int mid, int right) 
        // 拿到左半部分首元素下标
        int s1 = left;
        // 拿到右半部分首元素下标
        int s2 = mid + 1;
        // 临时数组：计算，存储归并后的数组，最后再进行赋值
        int[] temp = new int[right - left + 1];
        // 临时数组当前访问到的下标
        int index = 0;
        while (s1 <= mid && s2 <= right) 
            // 如果第一个数组的指针数值小于第二个数组的，那么其放置在临时空间上
            if (arr[s1] <= arr[s2]) 
                temp[index++] = arr[s1++];
             else     // 否则是第二个数组的数值放置于其上
                temp[index++] = arr[s2++];
            
        
        // 如果这是s1仍然没有到达其终点，那么说明它还有剩下，直接接上就好
        while (s1 <= mid) 
            temp[index++] = arr[s1++];
        
        while (s2 <= right) 
            temp[index++] = arr[s2++];
        
        // 数组复制
        for (int i = 0; i < temp.length; i++) 
            arr[i + left] = temp[i];
        
    

时间复杂度

接下来是一些奇怪的名词就冒出来了

二路归并

二路归并排序就是将两个有序子表归并成一个有序表，也就是说二路归并其实就是上面的归并排序，也是我们常用的。

就比如下面的归并：

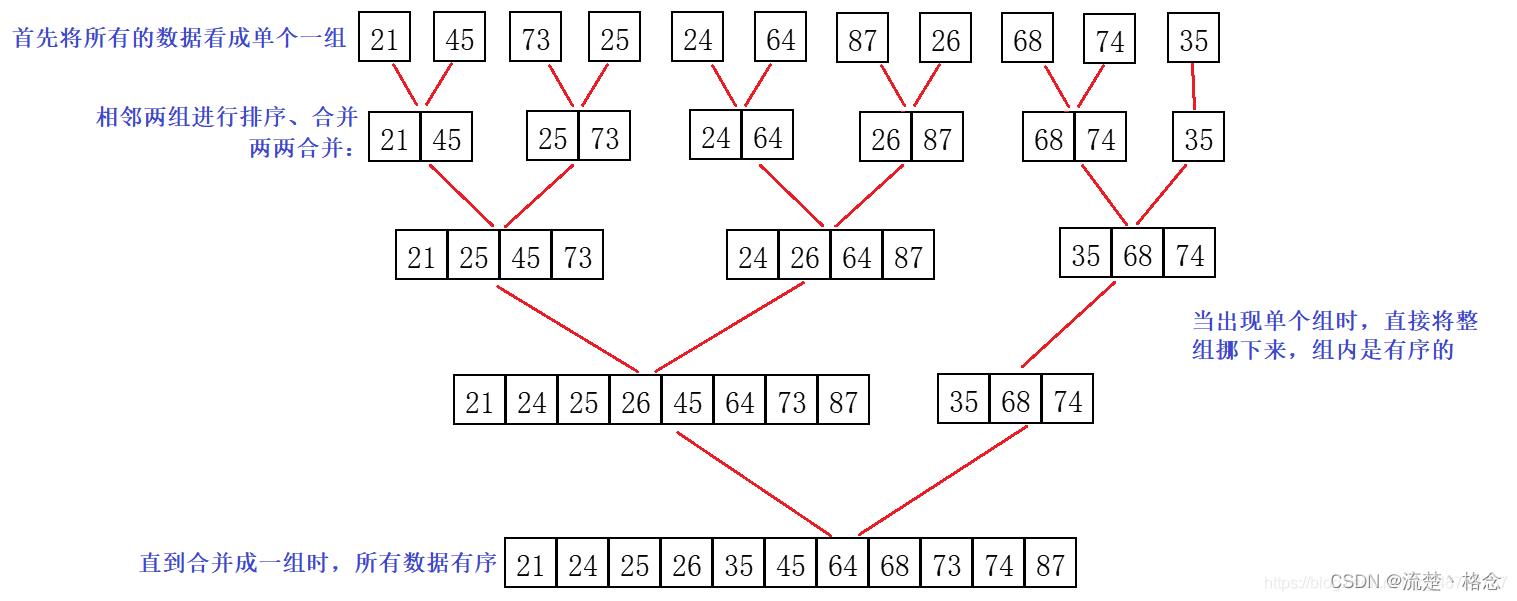
多路归并（三路为例）：

在上面的过程中，我们将序列分成两份。

那么尝试将序列均分为三段然后合并三个有序序列，这就是三路归并。

如果能将序列分成自然对数的底数 e 份所得的效率是这类分治然后合并的排序能得到的最好效率，但是 e≈2.718281828459，相对于 2，其与 3 更接近。

考虑合并的过程，每个元素只被加入临时数组一次，为 O(n) 的。

利用主定理 ：

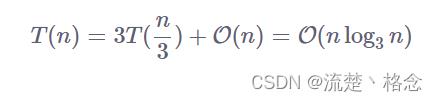
归并部分的代码如下：

void threeMergeSort(int *a,int l,int r) 
	if(l >= r) return ;
	static int t[N];
	int mid1 = l + (r - l) / 3,mid2 = r - (r - l) / 3;
	QytMergeSort(a,l,mid1);
	QytMergeSort(a,mid1 + 1,mid2);
	QytMergeSort(a,mid2 + 1,r);
	int p = l,p1 = l,p2 = mid1 + 1,p3 = mid2 + 1;
	while(p1 <= mid1 && p2 <= mid2 && p3 <= r) 
		if(a[p1] <= a[p2] && a[p1] <= a[p3])
			t[p++] = a[p1++];
		else if(a[p2] <= a[p1] && a[p2] <= a[p3])
			t[p++] = a[p2++];
		else
			t[p++] = a[p3++];
	
	
	while(p1 <= mid1 && p2 <= mid2) 
		if(a[p1] < a[p2]) t[p++] = a[p1++];
		else t[p++] = a[p2++];
	
	while(p1 <= mid1 && p3 <= r) 
		if(a[p1] < a[p3]) t[p++] = a[p1++];
		else t[p++] = a[p3++];
	
	while(p2 <= mid2 && p3 <= r) 
		if(a[p2] < a[p3]) t[p++] = a[p2++];
		else t[p++] = a[p3++];
	
	
	while(p1 <= mid1) t[p++] = a[p1++];
	while(p2 <= mid2) t[p++] = a[p2++];
	while(p3 <= r) t[p++] = a[p3++];
	rep(i,l,r) a[i] = t[i];

归并趟数

趟数说的是。

一趟排序最多可以排两个数据，即左边一个单元和右边一个单元归并到一个单元中。
两趟排序最多可以排四个数据，即一趟排好的两个单元归并到一个单元中。
……
……

过程如下：

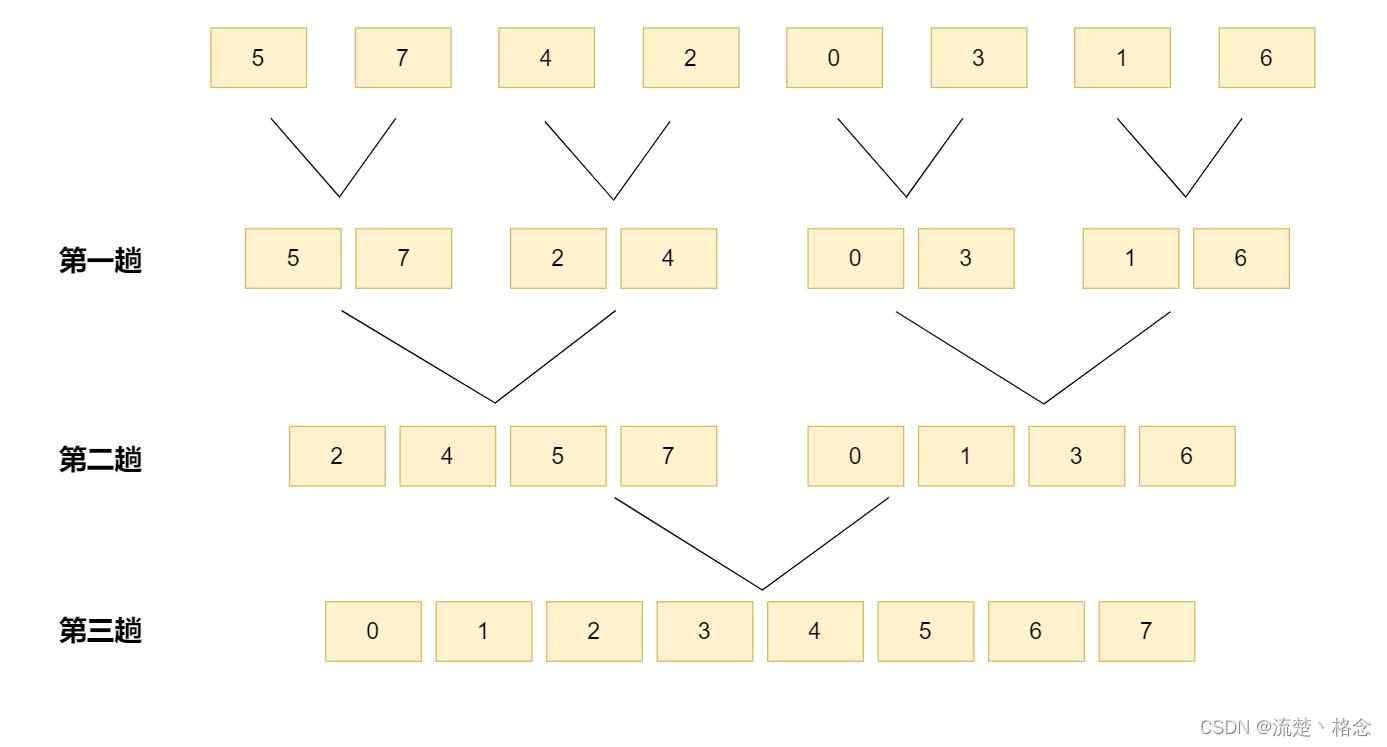
k趟排序最多可以排2的k次方个元素。

这里是8个元素，2的三次方是8，也就是这个数组最多是三趟

k趟排序最少可以排2的（k-1）次方个元素。
假设要排n个元素，则
2^(k-1) < n <=2^k
解得 k-1< log n <=k
即为 log n 往上取整