算法和数据结构解析-9 : 排序相关问题讲解
Posted 鮀城小帅
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了算法和数据结构解析-9 : 排序相关问题讲解相关的知识,希望对你有一定的参考价值。
1. 排序算法复习
常见的排序算法可以分为两大类:比较类排序,和非比较类排序。
- 比较类排序:通过比较来决定元素间的相对次序,由于其时间复杂度不能突破O(nlogn),因此也称为非线性时间比较类排序。
- 非比较类排序:不通过比较来决定元素间的相对次序,它可以突破基于比较排序的时间下界,以线性时间运行,因此也称为线性时间非比较类排序。主要思路是通过将数值以哈希(hash)或分桶(bucket)的形式直接映射到存储空间来实现的。
算法复杂度总览
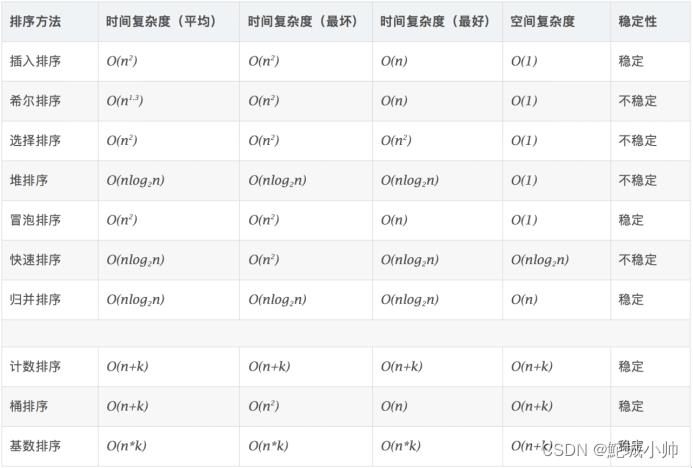
1.1 选择排序(Selection Sort)
选择排序是一种简单直观的排序算法。
它的工作原理:首先在未排序序列中找到最小(大)元素,存放到排序序列的起始位置,然后,再从剩余未排序元素中继续寻找最小(大)元素,然后追加到已排序序列的末尾。以此类推,直到所有元素均排序完毕。
1.2 冒泡排序(Bubble Sort)
冒泡排序也是一种简单的排序算法。
它的基本原理是:重复地扫描要排序的数列,一次比较两个元素,如果它们的大小顺序错误,就把它们交换过来。这样,一次扫描结束,我们可以确保最大(小)的值被移动到序列末尾。
这个算法的名字由来,就是因为越小的元素会经由交换,慢慢“浮”到数列的顶端。
1.3 插入排序
插入排序的算法,同样描述了一种简单直观的排序。
它的工作原理是:构建一个有序序列。对于未排序数据,在已排序序列中从后向前扫描,找到相应位置并插入。
以上三种简单排序算法,因为需要双重循环,所以时间复杂度均为O(n^2)。排序过程中,只需要额外的常数空间,所以空间复杂度均为O(1)。
1.4 希尔排序(Shell Sort)
1959年由Shell发明,是第一个突破O(n2)的排序算法,是简单插入排序的改进版。
它与插入排序的不同之处在于,它会优先比较距离较远的元素。希尔排序又叫缩小增量排序。
希尔排序在数组中采用跳跃式分组的策略,通过某个增量将数组元素划分为若干组,然后分组进行插入排序,随后逐步缩小增量,继续按组进行插入排序操作,直至增量为1。
希尔排序中对于增量序列的选择十分重要,直接影响到希尔排序的性能。一些经过优化的增量序列如Hibbard经过复杂证明可使得最坏时间复杂度为O(n^3/2)。
1.5 归并排序(Merge Sort)
归并排序是建立在归并操作上的一种有效的排序算法。该算法是采用分治法(Divide and Conquer)的一个非常典型的应用。
将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。若将两个有序表合并成一个有序表,称为2-路归并。
归并排序的时间复杂度是O(nlogn)。代价是需要额外的内存空间。
1.6 快速排序(Quick Sort)
快速排序的基本思想:通过一趟排序,将待排记录分隔成独立的两部分,其中一部分记录的关键字均比另一部分的关键字小,则可分别对这两部分记录继续进行排序,以达到整个序列有序。
可以看出,快排也应用了分治思想,一般会用递归来实现。
快速排序使用分治法来把一个串(list)分为两个子串(sub-lists)。具体算法描述如下:
- 从数列中挑出一个元素,称为 “基准”(pivot,中心,支点);
- 重新排序数列,所有元素比基准值小的摆放在基准前面,所有元素比基准值大的摆在基准的后面(相同的数可以到任一边)。这个称为分区(partition)操作。在这个分区退出之后,该基准就处于数列的中间位置(它应该在的位置);
- 递归地(recursive)把小于基准值元素的子数列,和大于基准值元素的子数列排序。
这里需要注意,分区操作在具体实现时,可以设置在序列首尾设置双指针,然后分别向中间移动;左指针找到最近的一个大于基准的数,右指针找到最近一个小于基准的数,然后交换这两个数。
package com.atguigu.algorithm.sort;
public class QuickSort
// 快排核心算法,递归调用
public static void qSort(int[] nums, int start, int end)
// 基准情况
if (start >= end) return;
// 1. 找到一个pivot,把数组划分成两部分,返回pivot索引位置
int index = partition(nums, start, end);
// 2. 递归排序左右两部分
qSort(nums, start, index - 1);
qSort(nums, index + 1, end);
// 分区方法
public static int partition1(int[] nums, int start, int end)
int pivot = nums[start]; // 以第一个元素作为中心点
// 定义双指针
int left = start, right = end;
// 要返回的pivot位置索引
int position = start;
while (left < right)
// 左指针向右移,找到一个比pivot大的数,就停下来
while (left < right && nums[left] <= pivot)
left ++;
while (left < right && nums[right] >= pivot)
right --;
// 判断左右指针是否相遇,如果没有相遇,交换两个元素
if (left < right)
swap(nums, left, right);
else
// 如果已经相遇,填入pivot
// 要判断当前位置和pivot的大小,确定到底填入哪个位置
if ( nums[left] < pivot)
position = left;
swap(nums, start, left);
else
position = left - 1;
swap(nums, start, left - 1);
return position;
public static int partition(int[] nums, int start, int end)
int pivot = nums[start];
int left = start, right = end;
while (left < right)
// 左移右指针,找到一个比pivot小的数,填入空位
while (left < right && nums[right] >= pivot)
right --;
nums[left] = nums[right];
while (left < right && nums[left] <= pivot)
left ++;
nums[right] = nums[left];
nums[left] = pivot;
return left;
public static void swap(int[] nums, int i, int j)
int temp = nums[i];
nums[i] = nums[j];
nums[j] = temp;
public static void main(String[] args)
int[] nums = 3, 45, 78, 36, 52, 11, 39, 36, 52;
qSort(nums, 0, nums.length - 1);
printArray(nums);
public static void printArray(int[] arr)
for (int num: arr)
System.out.print(num + "\\t");
System.out.println();
快速排序的时间复杂度可以做到O(nlogn),在很多框架和数据结构设计中都有广泛的应用。
1.7 堆排序(Heap Sort)
堆排序是指利用堆这种数据结构所设计的一种排序算法。
堆(Heap)是一个近似完全二叉树的结构,并同时满足堆的性质:即子结点的键值或索引总是小于(或者大于)它的父节点。
一般情况,将堆顶元素为最大值的叫做“大顶堆”(Max Heap),堆顶为最小值的叫做“小顶堆”。
算法简单来说,就是构建一个大顶堆,取堆顶元素作为当前最大值,然后删掉堆顶元素、将最后一个元素换到堆顶位置,进而不断调整大顶堆、继续寻找下一个最大值。
这个过程有一些类似于选择排序(每次都选取当前最大的元素),而由于用到了二叉树结构进行大顶堆的调整,时间复杂度可以降为O(nlogn)。
1.8 计数排序(Counting Sort)
计数排序不是基于比较的排序算法,其核心在于将输入的数据值转化为键存储在额外开辟的数组空间中。作为一种线性时间复杂度的排序,计数排序要求输入的数据必须是有确定范围的整数。
简单来说,就是要找到待排序数组中的最大和最小值,得到所有元素可能的取值范围;然后统计每个值出现的次数。统计完成后,只要按照取值顺序、依次反向填充目标数组就可以了。
计数排序时间复杂度是O(n+k),空间复杂度也是O(n+k),其排序速度快于任何比较排序算法。当k不是很大并且序列比较集中时,计数排序是一个很有效的排序算法。
1.9 桶排序(Bucket Sort)
桶排序是计数排序的升级版。它利用了函数的映射关系,高效与否的关键就在于映射函数的确定。
桶排序 (Bucket sort)的工作原理:假设输入数据服从均匀分布,将数据分到有限数量的桶里,每个桶再分别排序。
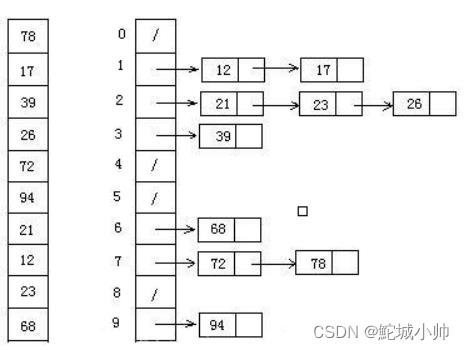
桶排序最好情况下使用线性时间O(n)。
桶排序的时间复杂度,取决与对各个桶之间数据进行排序的时间复杂度,因为其它部分的时间复杂度都为O(n)。很显然,桶划分的越小,各个桶之间的数据越少,排序所用的时间也会越少。但相应的空间消耗就会增大。
1.10 基数排序(Radix Sort)
基数排序可以说是桶排序的扩展。
算法原理是按照低位先排序,然后收集;再按照高位排序,然后再收集;依次类推,直到最高位。
最常见的做法,就是取10个桶,数值最高有几位,就按照数位排几次。例如:

第一次排序:按照个位的值,将每个数保存到对应的桶中:
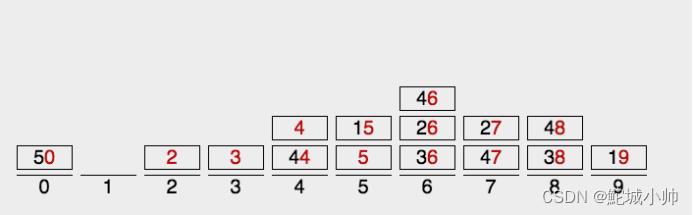
将桶中的数据依次读出,填充到目标数组中,这时可以保证后面的数据,个位一定比前面的数据大。
第二次排序:按照十位的值,将每个数保存到对应的桶中: 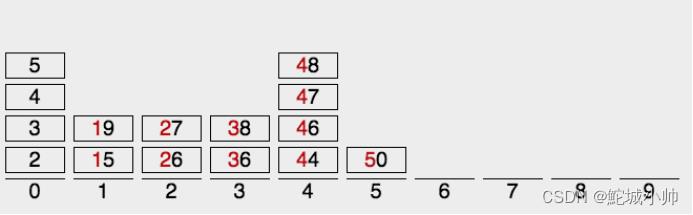
因为每个桶中的数据,都是按照个位从小到大排序的,所以再次顺次读出每个桶中的数据,就得到了完全排序的数组:

基数排序的空间复杂度为O(n+k),其中k为桶的数量。一般来说n>>k,因此额外空间需要大概n个左右。
2. 数组中的第K个最大元素
2.1 题目说明
在未排序的数组中找到第 k 个最大的元素。请注意,你需要找的是数组排序后的第 k 个最大的元素,而不是第 k 个不同的元素。
示例 1:
输入: [3,2,1,5,6,4] 和 k = 2
输出: 5
示例 2:
输入: [3,2,3,1,2,4,5,5,6] 和 k = 4
输出: 4
说明:
你可以假设 k 总是有效的,且 1 ≤ k ≤ 数组的长度。
2.2 分析
要寻找数组中第K大的元素,首先能想到的,当然就是直接排序。只要数组是有序的,那么接下来取出倒数第K个元素就可以了。
public class KthLargestElement
// 方法一:直接排序(调库)
public int findKthLargest1(int[] nums, int k)
Arrays.sort(nums);
return nums[nums.length - k];
我们知道,java的Arrays.sort()方法底层就是快速排序,所以时间复杂度为O(nlogn)。
如果实际遇到这个问题,直接调类库方法去排序,显然是不能让面试官满意的。我们应该手动写出排序的算法。
选择、冒泡和插入排序时间复杂度是O(n^2),性能较差;二计数排序、桶排序和基数排序尽管时间复杂度低,但需要占用大量的额外空间,而且只有在数据取值范围比较集中、桶数较少时效率比较高。所以实际应用中,排序的实现算法一般采用快速排序,或者归并和堆排序。
对于这道题目而言,其实还可以进一步优化:因为我们只关心第K大的元素,其它位置的元素其实可以不排。
基于这样的想法,显然归并这样的算法就无从优化了;但快排和堆排序可以。
2.3 方法一:基于快速排序的选择
我们可以改进快速排序算法来解决这个问题:在分区(partition)的过程当中,我们会对子数组进行划分,如果划分得到的位置 q 正好就是我们需要的下标,就直接返回 a[q];否则,如果 q 比目标下标小,就递归右子区间,否则递归左子区间。这样就可以把原来递归两个区间变成只递归一个区间,提高了时间效率。这就是“快速选择”算法。
另外,我们知道快速排序的性能和“划分”出的子数组的长度密切相关。我们可以引入随机化来加速这个过程,它的时间代价的期望是 O(n)。
// 方法二:基于快排的选择
public int findKthLargest2(int[] nums, int k)
return quickSelect(nums, 0, nums.length - 1, nums.length - k );
// 实现快速选择方法
public int quickSelect(int[] nums, int start, int end, int index)
// 找到pivot的位置返回
int position = randomPatition(nums, start, end);
// 判断当前pivot位置是否为index
if (position == index)
return nums[position];
else
return position > index ? quickSelect(nums, start, position - 1, index): quickSelect(nums, position + 1, end, index);
// 实现一个随机分区方法
public int randomPatition(int[] nums, int start, int end)
Random random = new Random();
int randIndex = start + random.nextInt(end - start + 1); // 随机生成pivot的位置
swap(nums, start, randIndex);
return partition(nums, start, end);
public static int partition(int[] nums, int start, int end)
int pivot = nums[start];
int left = start, right = end;
while (left < right)
// 左移右指针,找到一个比pivot小的数,填入空位
while (left < right && nums[right] >= pivot)
right --;
nums[left] = nums[right];
while (left < right && nums[left] <= pivot)
left ++;
nums[right] = nums[left];
nums[left] = pivot;
return left;
public static void swap(int[] nums, int i, int j)
int temp = nums[i];
nums[i] = nums[j];
nums[j] = temp;
复杂度分析
时间复杂度:O(n),证明过程可以参考《算法导论》9.2:期望为线性的选择算法。
空间复杂度:O(logn),递归使用栈空间的空间代价的期望为O(logn)。
2.4 方法二:基于堆排序的选择
我们也可以使用堆排序来解决这个问题。
基本思路是:构建一个大顶堆,做 k−1 次删除操作后堆顶元素就是我们要找的答案。
在很多语言中,都有优先队列或者堆的的容器可以直接使用,但是在面试中,面试官更倾
// 方法三:基于堆排序的选择
public int findKthLargest(int[] nums, int k)
int n = nums.length;
// 保存堆的大小,初始就是n
int heapSize = n;
// 1. 构建大顶堆
buildMaxHeap(nums, heapSize);
// 2. 执行k-1次删除堆顶元素操作
for (int i = n - 1; i > n - k; i--)
// 将堆顶元素交换到当前堆的末尾
swap(nums, 0, i);
heapSize --;
maxHeapify(nums, 0, heapSize);
// 3. 返回当前堆顶元素
return nums[0];
// 实现一个构建大顶堆的方法
public void buildMaxHeap(int[] nums, int heapSize)
for (int i = heapSize / 2 - 1; i >= 0; i --)
maxHeapify(nums, i, heapSize);
// 定义一个调整成大顶堆的方法
public void maxHeapify(int[] nums, int top, int heapSize)
// 定义左右子节点
int left = top * 2 + 1;
int right = top * 2 + 2;
// 保存当前最大元素的索引位置
int largest = top;
// 比较左右子节点,记录最大元素索引位置
if (right < heapSize && nums[right] > nums[largest])
largest = right;
if (left < heapSize && nums[left] > nums[largest])
largest = left;
// 将最大元素换到堆顶
if ( largest != top )
QuickSort.swap(nums, top, largest);
// 递归调用,继续下沉
maxHeapify(nums, largest, heapSize);
复杂度分析
时间复杂度:O(nlogn),建堆的时间代价是 O(n),k-1次删除的总代价是 O(klogn),因为 k<n,故渐进时间复杂为 O(n+klogn)=O(nlogn)。
空间复杂度:O(logn),即递归使用栈空间的空间代价。
3. 颜色分类
3.1 题目说明
给定一个包含红色、白色和蓝色,一共 n 个元素的数组,原地对它们进行排序,使得相同颜色的元素相邻,并按照红色、白色、蓝色顺序排列。
此题中,我们使用整数 0、 1 和 2 分别表示红色、白色和蓝色。
进阶:
- 你可以不使用代码库中的排序函数来解决这道题吗?
- 你能想出一个仅使用常数空间的一趟扫描算法吗?
示例 1:
输入:nums = [2,0,2,1,1,0]
输出:[0,0,1,1,2,2]
示例 2:
输入:nums = [2,0,1]
输出:[0,1,2]
示例 3:
输入:nums = [0]
输出:[0]
示例 4:
输入:nums = [1]
输出:[1]
提示:
- n == nums.length
- 1 <= n <= 300
- nums[i] 为 0、1 或 2
3.2 分析
本题是经典的“荷兰国旗问题”,由计算机科学家 Edsger W. Dijkstra 首先提出。
荷兰国旗是由红白蓝3种颜色的条纹拼接而成,如下图所示

假设这样的条纹有多条,且各种颜色的数量不一,并且随机组成了一个新的图形,新的图形可能如下图所示,但是绝非只有这一种情况:

需求是:把这些条纹按照颜色排好,红色的在上半部分,白色的在中间部分,蓝色的在下半部分,我们把这类问题称作荷兰国旗问题。
本题其实就是荷兰国旗问题的数学描述,它在本质上,其实就是就是一个有重复元素的排序问题。所以可以用排序算法来解决。
当然,最简单的方式,就是直接调Java已经内置的排序方法:
public void sortColors(int[] nums)
Arrays.sort(nums);
时间复杂度为O(nlogn)。但显然这不是我们想要的,本题用到的排序算法应该自己实现,而且要根据本题的具体情况进行优化。
3.3 方法一:基于选择排序
如果用选择排序的思路,我们可以通过遍历数组,找到当前最小(或最大的数)。
对于本题,因为只有0,1,2三个值,我们不需要对每个位置的“选择”都遍历一遍数组,而是最多遍历三次就够了:第一次遍历,把扫描到的0全部放到数组头部;第二次遍历,把所有1跟在后面;最后一次,把所有2跟在最后。
事实上,最后对于2的扫描已经没有必要了:因为除了0和1,剩下的位置一定都是2。所以我们可以用两次扫描,实现这个算法。
// 方法二:基于选择排序
public void sortColors2(int[] nums)
// 定义一个指针,指向当前应该填入元素的位置
int curr = 0;
// 1. 遍历数组,将所有0交换到数组头部
for (int i = 0; i < nums.length; i ++)
if (nums[i] == 0)
swap(nums, curr ++, i);
// 2. 遍历数组,将所有1交换到中间位置,接着之前的curr继续
for (int i = 0; i < nums.length; i ++)
if (nums[i] == 1)
swap(nums, curr ++, i);
public static void swap(int[] nums, int i, int j)
int temp = nums[i];
nums[i] = nums[j];
nums[j] = temp;
复杂度分析
时间复杂度:O(n),n为数组nums的长度。需要遍历两次数组。
空间复杂度:O(1),只用到了常数个辅助变量。
3.4 方法二:基于计数排序
根据题目中的提示,要排序的数组中,其实只有0,1,2三个值。
所以另一种思路是,我们可以直接统计出数组中 0,1,2 的个数,再根据它们的数量,重写整个数组。这其实就是计数排序的思路。
// 方法三:基于计数排序
public void sortColors3(int[] nums)
int count0 = 0, count1 = 0;
// 遍历数组,统计0,1,2的个数
for (int num: nums)
if (num == 0)
count0 ++;
else if (num == 1)
count1 ++;
// 将0,1,2按照个数依次填入nums数组
for (int i = 0; i < nums.length; i++)
if (i < count0)
nums[i] = 0;
else if (i < count0 + count1)
nums[i] = 1;
else
nums[i] = 2;
复杂度分析
时间复杂度:O(n),n为数组nums的长度。需要遍历两次数组。
空间复杂度:O(1),只用到了常数个辅助变量。
3.5 方法三:基于快速排序
前面的算法,尽管时间复杂度为O(n),但都进行了两次遍历。能不能做一些优化,只进行一次遍历就解决问题呢?
一个思路是,使用双指针。所有的0移到数组头,所有2移到数组尾,1保持不变就可以了。这其实就是快速排序的思路。
// 方法四:基于快速排序
public void sortColors(int[] nums)
// 定义左右指针
int left = 0, right = nums.length - 1;
// 定义一个遍历所有元素的指针
int i = left;
// 循环判断,遍历元素
while (left < right && i <= right)
// 1. 如果是2,换到末尾,右指针左移
while (i <= right && nums[i] == 2)
QuickSort.swap(nums, i, right --);
// 2. 如果是0,换到头部,左指针右移
if (nums[i] == 0)
QuickSort.swap(nums, i, left ++);
// 3. i++,继续遍历
i++;
复杂度分析
时间复杂度:O(n),n为数组nums的长度。双指针法只虚遍历一次数组。
空间复杂度:O(1),只用到了常数个辅助变量。
4. 合并区间
4.1 题目说明
给出一个区间的集合,请合并所有重叠的区间。
示例 1:
输入: intervals = [[1,3],[2,6],[8,10],[15,18]]
输出: [[1,6],[8,10],[15,18]]
解释: 区间 [1,3] 和 [2,6] 重叠, 将它们合并为 [1,6].
示例 2:
输入: intervals = [[1,4],[4,5]]
输出: [[1,5]]
解释: 区间 [1,4] 和 [4,5] 可被视为重叠区间。
提示:
- intervals[i][0] <= intervals[i][1]
4.2 分析
要判断两个区间[a1, b1], [a2, b2]是否可以合并,其实就是判断是否有a1 <= a2 <= b1,或者a2 <= a1 <= b2。也就是说,如果某个子区间的左边界在另一子区间内,那么它们可以合并。
4.3 解决方法:排序
一个简单的想法是,我们可以遍历每一个子区间,然后判断它跟其它区间是否可以合并。如果某两个区间可以合并,那么就把它们合并之后,再跟其它区间去做判断。
很明显,这样的暴力算法,时间复杂度不会低于O(n^2)。有没有更好的方式呢?
这里我们发现,判断区间是否可以合并的关键,在于它们左边界的大小关系。所以我们可以先把所有区间,按照左边界进行排序。
那么在排完序的列表中,可以合并的区间一定是连续的。如下图所示,标记为蓝色、黄色和绿色的区间分别可以合并成一个大区间,它们在排完序的列表中是连续的:

具体代码如下:
import java.util.ArrayList;
import java.util.Arrays;
import java.util.Comparator;
public class MergeIntervals
// 按区间左边界排序
public int[][] merge(int[][] intervals)
// 定义一个结果数组
ArrayList<int[]> result = new ArrayList<>();
// 1. 将所有区间按照左边界排序
Arrays.sort(intervals, new Comparator<int[]>()
@Override
public int compare(int[] o1, int[] o2)
return o1[0] - o2[0];
);
// 2. 遍历排序后的区间,逐个合并
for (int[] interval: intervals)
// 记录当前的左右边界
int left = interval[0], right = interval[1];
// 获取结果数组长度
int length = result.size();
// 如果left比最后一个区间的右边界大,不能合并,直接添加到结果
if ( length == 0 || left > result.get(length-1)[1] )
result.add(interval);
else
// 可以合并
int mergedLeft = result.get(length-1)[0];
int mergedRight = Math.max(result.get(length-1)[1], right);
result.set(length - 1, new int[]mergedLeft, mergedRight);
return result.toArray(new int[result.size()][]);
public static void main(String[] args)
int[][] intervals = 1,3,2,6,8,10,15,18;
MergeIntervals mergeIntervals = new MergeIntervals();
for (int[] interval: mergeIntervals.merge(intervals))
QuickSort.printArray(interval);
复杂度分析
时间复杂度:O(nlogn),其中 n 为区间的数量。除去排序的开销,我们只需要一次线性扫描,所以主要的时间开销是排序的 O(nlogn)。
空间复杂度:O(logn),其中 n 为区间的数量。O(logn) 即为快速排序所需要的空间复杂度(递归栈深度)。
以上是关于算法和数据结构解析-9 : 排序相关问题讲解的主要内容,如果未能解决你的问题,请参考以下文章