人工智能数学基础--概率与统计8：一个很有意思的下棋输赢概率问题

Posted 2022-11-04 LaoYuanPython

一、问题

甲、乙二人下象棋，每局甲胜的概率为a，乙胜的概率为b。为简化问题，设没有和局的情况，这意味着a+b=1。设想甲的棋艺高于乙，即a>b。考虑到这个情况，他们商定最终胜负的规则如下：
到什么时候为止甲连胜了三局而在此之前乙从未连胜二局，则甲胜;反之，若到什么时候为止乙连胜了二局而在此之前甲从未连胜三局，则乙胜。

求“甲最终取胜”这个事件A的概率P(A)及“乙最终取胜”这个事件B的概率P(B)。

二、求解甲胜的概率过程

为方便计，分别以E和F表示甲、乙在特定的一局取胜的事件，有P(E)=a，P(F)=b。现考虑“甲取胜”的事件 A，分两种情况：

1. 第一局甲胜而最终甲胜了
   这一情况又可分解为许多子情况:对n=0，1，2，···，甲经过n个“阶段”后才取胜，每个阶段是 EF 或EEF（注意：为了与下一阶段互相独立，一定要确保最后一个是F），然后接着来一个EEE。例如，甲经过3个阶段后获胜的一种可能实战结果为：EEF EFEEF EEE
   即共下了11局甲才获胜，其中第1，2，4，6，7，9，10，11局甲胜，其余乙胜。每个阶段不是EF 就是EEF，这两种情况互斥，又由独立性，知每个阶段的概率为ab+aab=ab(1+a)。
   再由独立性，知“经n个阶段后甲获胜”的概率为。[ab(1+a)]ⁿa³,n可以为0，1，2，···，不同的n 互斥，于是这部分概率总和为
   
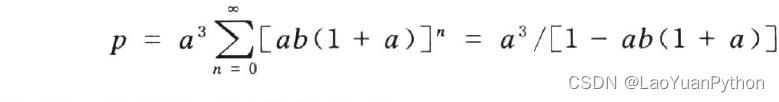
   关于这个求和结果不清楚的可以参考《转载：等比数列的求和公式，及其推导过程》算出等比数列和，在利用b=1-a及极限的知识即可求得。
2. 第一局乙胜而最终甲胜了
   既然第一局为F而最终甲胜，则第二局必须是E。故以第二局作起点看，我们回到了情况1，从而这部分的概率为bp，请注意，这里事实上已用了概率的乘法定理：
   P(第一局乙胜且最终甲胜)=P(第一局乙胜)P(第二局甲胜且最终甲胜)
   P(第一局乙胜) = b，P(第二局甲胜且最终甲胜) =p。综合两个情况(它们互斥)，由概率加法定理得：
   

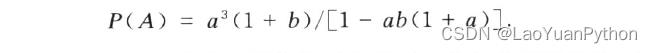
三、求解乙胜的概率过程

求乙胜的概率过程与求甲胜的概率过程类似，不过需要分三种情况：

1. 第一局乙胜，分为n+1个阶段，前n个阶段每个阶段是FEE或FEFE，最后一个阶段是FF，前n个阶段每阶段的概率是a²b（1+b）,最后一阶段是b²，可以求得这种情况的概率为：P(B) = b²Σ（ab+a²b）ⁿ=b²/(1-ab(1+a))；
2. 第一局甲胜，第二局乙胜，这个从第二局开始就是第一种情况，因此其概率为ab²/(1-ab(1+a))；
3. 前两局甲胜，这个从第二局开始就是第二种情况，因此其概率为a²b²/(1-ab(1+a))。

最终乙胜的概率为：（b²+ab²+a²b²）/（1-ab（1+a)）,由于a+b=1，可以计算得到:P(A)+P(B)=1。

四、小结

本文是根据陈希孺版《概率论与数理统计》《第一章事件的概率》结合老猿自己的理解介绍的，大部分内容来自书中原文，但补充了两方面的内容，一是求甲胜的概率的等比数列求和式子的结果的计算原理，二是求乙胜的每种情况的概率计算过程和结果。

这个例子值得细心品味。第一，它提供了一个涉及无限个事件的情况(在甲最终取胜前可以经过任意多的“阶段”)，以及在无穷个事件时使用概率加法定理。第二，本例告诉我们，在面对一个复杂事件时，主要的方法是冷静地分析，以设法把它分拆成一些互斥的简单情况。这里，必须细心确保互斥性又无遗漏，一着不慎，满盘皆非。

更多人工智能数学基础请参考专栏《人工智能数学基础》。

写博不易，敬请支持：

如果阅读本文于您有所获，敬请点赞、评论、收藏，谢谢大家的支持！

关于老猿的付费专栏

1. 付费专栏《https://blog.csdn.net/laoyuanpython/category_9607725.html 使用PyQt开发图形界面Python应用》专门介绍基于Python的PyQt图形界面开发基础教程，对应文章目录为《 https://blog.csdn.net/LaoYuanPython/article/details/107580932 使用PyQt开发图形界面Python应用专栏目录》；
2. 付费专栏《https://blog.csdn.net/laoyuanpython/category_10232926.html moviepy音视频开发专栏 )详细介绍moviepy音视频剪辑合成处理的类相关方法及使用相关方法进行相关剪辑合成场景的处理，对应文章目录为《https://blog.csdn.net/LaoYuanPython/article/details/107574583 moviepy音视频开发专栏文章目录》；
3. 付费专栏《https://blog.csdn.net/laoyuanpython/category_10581071.html OpenCV-Python初学者疑难问题集》为《https://blog.csdn.net/laoyuanpython/category_9979286.html OpenCV-Python图形图像处理 》的伴生专栏，是笔者对OpenCV-Python图形图像处理学习中遇到的一些问题个人感悟的整合，相关资料基本上都是老猿反复研究的成果，有助于OpenCV-Python初学者比较深入地理解OpenCV，对应文章目录为《https://blog.csdn.net/LaoYuanPython/article/details/109713407 OpenCV-Python初学者疑难问题集专栏目录 》
4. 付费专栏《https://blog.csdn.net/laoyuanpython/category_10762553.html Python爬虫入门 》站在一个互联网前端开发小白的角度介绍爬虫开发应知应会内容，包括爬虫入门的基础知识，以及爬取CSDN文章信息、博主信息、给文章点赞、评论等实战内容。

前两个专栏都适合有一定Python基础但无相关知识的小白读者学习，第三个专栏请大家结合《https://blog.csdn.net/laoyuanpython/category_9979286.html OpenCV-Python图形图像处理 》的学习使用。

对于缺乏Python基础的同仁，可以通过老猿的免费专栏《https://blog.csdn.net/laoyuanpython/category_9831699.html 专栏：Python基础教程目录）从零开始学习Python。

如果有兴趣也愿意支持老猿的读者，欢迎购买付费专栏。

老猿Python，跟老猿学Python！

☞ ░ 前往老猿Python博文目录 https://blog.csdn.net/LaoYuanPython ░