模糊时间的柔性车间调度问题-Python实现遗传算法求解

Posted 2022-11-03 码丽莲梦露

目录

1 问题描述

1.1 模糊加工时间的运算

 2 编码解码

 3 算例

4 算法

4.1 文献【2】中算例验证

4 部分代码展示

完整代码：https://github.com/Aihong-Sun/FJSP_FP_GA

---

1 问题描述

        模糊性和灵活性的概念普遍存在于实际制造系统中，因为机器通常具有多种功能，并且无法提前不精确地知道处理时间。因此，研究具有模糊处理时间的柔性调度问题对于实际应用非常重要。        

        FJSPF（the FJSP with Fuzzy Processing time）可以表述如下：有n 个工件要在 m 台机器上加工。每个工件有ni个工序，每个工件必须按确定的路径完成所有工序，每道工序有1台及以上加工工序，工序的加工时间为模糊时间。

1.1 模糊加工时间的运算

        当工序加工时间为模糊时间时，要想能很好的排产出来，比如在甘特图上排产，需要一些模糊数运算操作。这些运算包括加法运算、两个模糊数的最大运算和模糊数的排序方法。加法运算用于计算运算的模糊完成时间。最大操作用于定义操作。另一种方法是比较最大模糊完成时间。

 对于两个三角模糊数（Triangle fuzzy numbers），和,

(1)加法操作：

(2)取大操作：为了衡量三角模糊书的大小关系,, Sakawa等[1]提出判定方法,此后又有许多学者 重新进行了定义. 本文采用Lei[2] 提出的判别规则, 令

 有: 

        1）若F(X)>F(Y),则X>Y.

        2)   若F(X)=F(Y),则比较,若,则X>Y

        3)   若F(X)=F(Y),且,则比较区间大小，如果,则X>Y

 2 编码解码

参考文献[3]

算例如下：

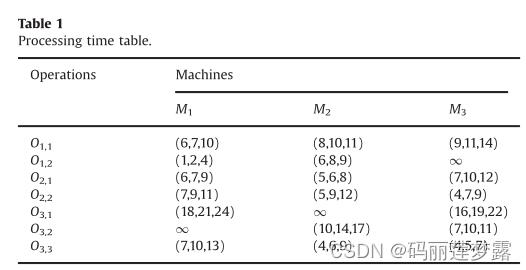
 编码：编码采用OSMS编码，不太知道的可以看我之前写的关于柔性作业车间调度的文章

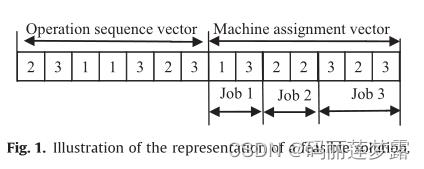
解码：

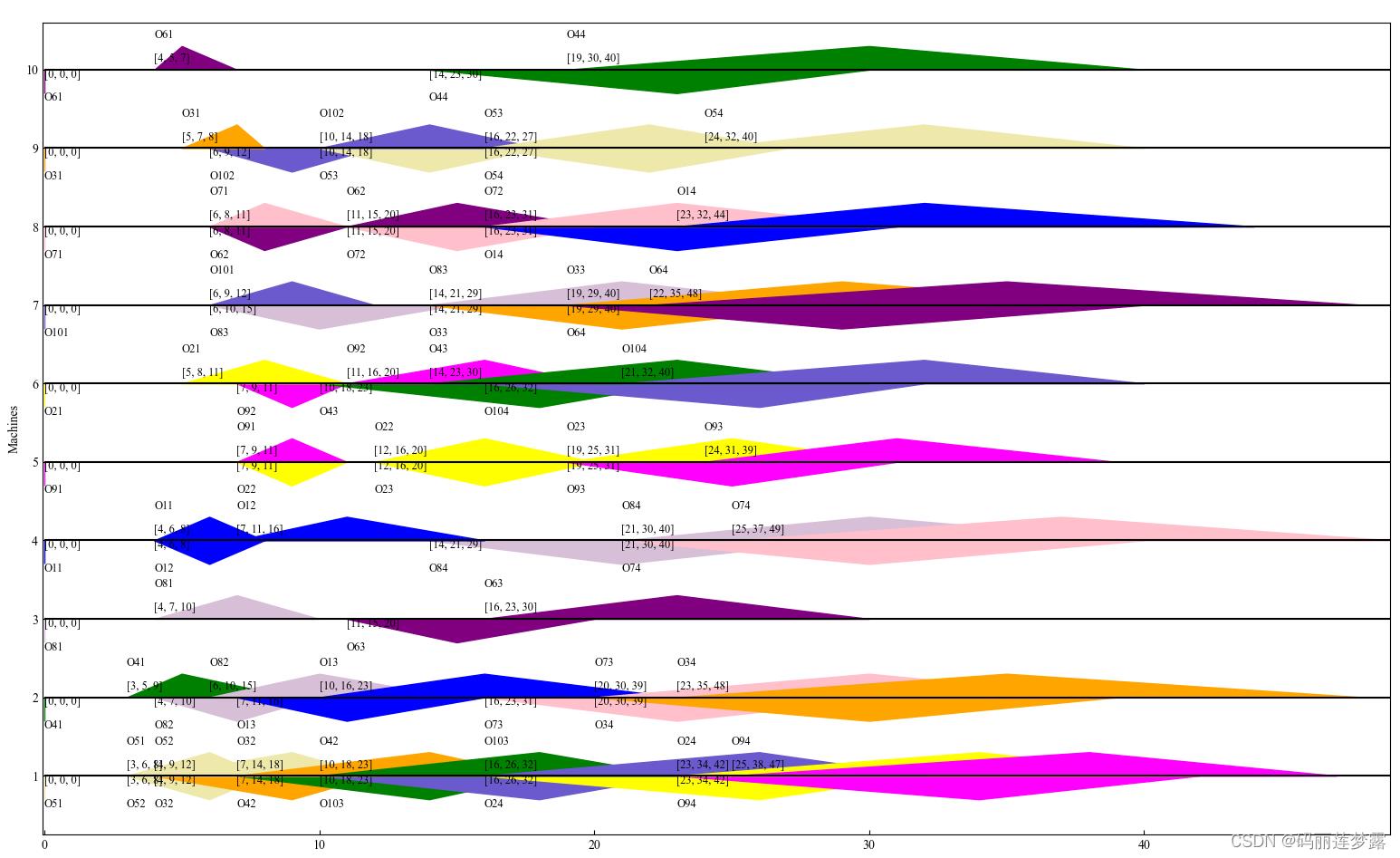
解码前，首先对三角模糊Gantt图进行说明，我们都知道，Gantt图是对各工序在每个机器上加工的开始结束时间进行可视化表述，同理三角模糊Gantt图也是如此，同一横线上的表示一个机器上的工序，横线下方为工序的模糊开始时间，横线上方为工序的模糊结束时间。

普通解码：从左到右读取OS、MS编码，不考虑插入，直接解码

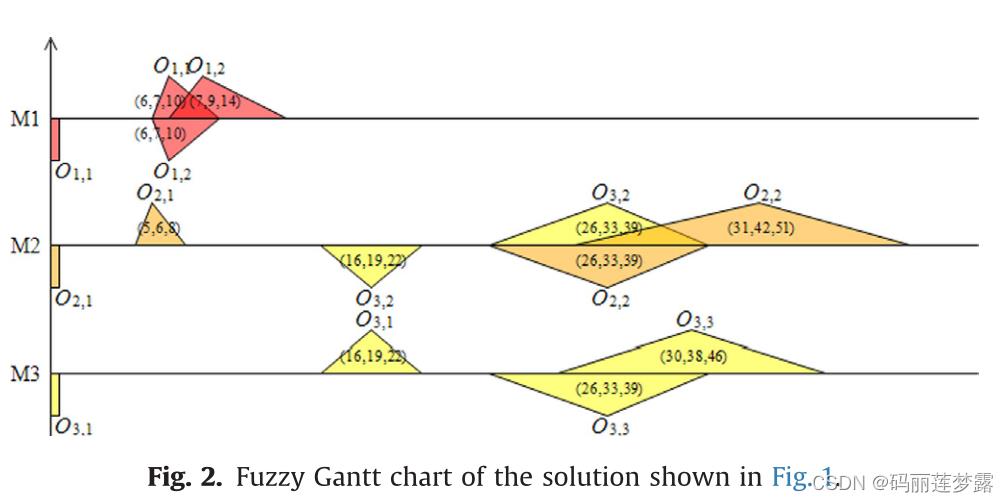
 贪婪解码：考虑工序前插（这跟普通FJSP问题差不多，唯一的区别在于，这里的工序时间是模糊时间）

上诉普通解码的考虑前插后变为：

适应度值为模糊完工时间的三角模糊数：

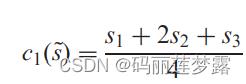
 3 算例

上面给出的文献【2】中提供了4个算例。（单目标），我也对算例进行了整理，需要的可前往此处获取：Aihong-Sun/Fuzzy_time_FJSP_Instance: Instance from <A genetic algorithm for flexible job shop scheduling with fuzzy processing time> (github.com)文献[3]中提供了以完工时间、加工成本、设备负载平衡和加工能耗为目标的多目标算例:

Fuzzy_time_FJSP_Instance/base_instance.py at main · Aihong-Sun/Fuzzy_time_FJSP_Instance (github.com)

4 算法

使用普通GA+精英保留策略（种群个数：100，迭代次数：100，交叉率：0.8，变异率：0.05，Elite个数：10）对算例进行了测试.

注：本文的交叉变异设置较为随意且未加任意局部搜索等，效果有差距属于正常，

4.1 文献【2】中算例验证

        文献2中对自己生成的算例的测试结果如下：

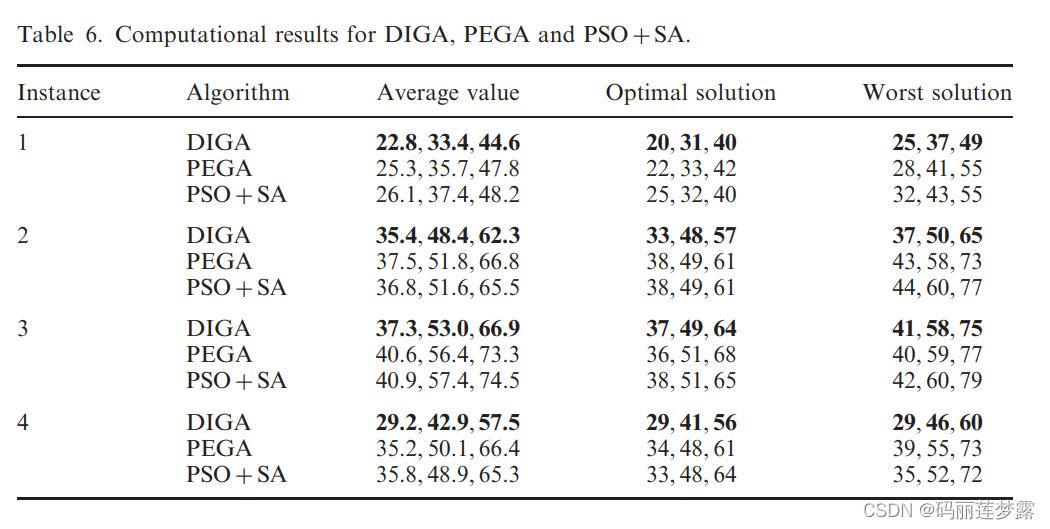
        本文用普通GA的测试10次得到的效果如下 ：

Instance	Best	worst	CPU(s)
1	[21,32,44]	[25,35,49]	4.19
2	[35,50,62]	[36,50,67]	4.06
3	[40,55,69]	[38,55,74]	5.53
4	[28,40,57]	[30,43,62]	5.52

参考文献：

[1]Sakawa M, Kubota R. Fuzzy programming for multiobjective job shop scheduling with fuzzy processing time and fuzzy duedate through genetic algorithms[J]. European Journal of Operational Research, 2000, 120(2): 393-407.

[2]Lei D M. A genetic algorithm for flexible job shop scheduling with fuzzy processing time[J]. International Journal of Production Research, 2010, 48(10): 2995-3013.

[3]Xu,,Ye,Wang,,Ling,Wang,,Sheng-yao,Liu,,& Min.(2015).An effective teaching-learning-based optimization algorithmfor the flexible job-shop scheduling problem with fuzzy processing time.NEUROCOMPUTING,148,260-268.

[4]郭钧,钟精诚,杜百岗等.考虑模糊作业时间的再制造加工车间多目标调度方法[J].控制与决策,2020,35(6):1497-1504.

4 部分代码展示

'''
by: Aihong-Sun
use for: Job describe
'''
from Flexible_Job_Shop.Job import Job
from Flexible_Job_Shop.Machine import Machine
from Fuzzy_Shop_Floor.Fuzzy_time_operator import *

class Job_fuzzy(Job):
    def __init__(self,idx,processing_machine,processing_time):
        super(Job_fuzzy, self).__init__(idx,processing_machine,processing_time)
        self.end=[0,0,0]

class Machine_fuzzy(Machine):
    def __init__(self, idx):
        super(Machine_fuzzy, self).__init__(idx)

    def update(self,s,e,Job):
        self.start.append(s)
        self.start.sort(key=lambda u:u[1])
        self.end.append(e)
        self.end.sort(key=lambda u:u[1])
        idx=self.start.index(s)
        self._on.insert(idx,Job)

    def find_start(self,s,o_pt):
        if self.end==[]: return s
        else:
            if Measure(s,self.end[-1]):return s
            else:
                o_s=self.end[-1]
                l = len(self.end) - 2
                while l>=0:
                    if Measure(add(s,o_pt),self.start[l+1]):
                        break
                    if Measure(self.end[l],s) and Measure(self.start[l+1],add(self.end[l],o_pt)):
                        o_s=self.end[l]
                    elif  Measure(s,self.end[l]) and Measure(self.start[l+1],add(s,o_pt)):
                        o_s=s
                    l-=1
                return o_s

'''
by: Aihong-Sun
use for: Job shop describe
'''
from Fuzzy_Shop_Floor.fuzzy_SF_Item import Job_fuzzy as Job
from Fuzzy_Shop_Floor.fuzzy_SF_Item import Machine_fuzzy as Machine
from Fuzzy_Shop_Floor.Fuzzy_time_operator import *

class Job_shop:
    def __init__(self,args):
        self.n= args.n
        self.m=args.m
        self.O_num=args.O_num
        self.PM = args.Processing_Machine
        self.PT = args.Processing_Time

    def reset(self):
        self.C_end=[0,0,0]
        self.C_max = 0
        self.Jobs=[]
        for i in range(self.n):
            Ji=Job(i,self.PM[i],self.PT[i])
            self.Jobs.append(Ji)
        self.Machines=[]
        for j in range(self.m):
            Mi=Machine(j)
            self.Machines.append(Mi)

    #Xu,,Ye,Wang,,Ling,Wang,,Sheng-yao,Liu,,& Min.(2015).An effective teaching-learning-based optimization algorithm
    # for the flexible job-shop scheduling problem with fuzzy processing time.NEUROCOMPUTING,148,260-268.
    def decode(self,Job,Machine):
        Ji=self.Jobs[Job]
        o_pt, s,M_idx = Ji.get_next_info(Machine)
        Mi=self.Machines[M_idx-1]
        start=Mi.find_start(s,o_pt)
        end=add(start,o_pt)
        Ji.update(end)
        Mi.update(start,end,[Ji.idx,Ji.cur_op])
        if Measure(end,self.C_end):
            self.C_end=end
            self.C_max=TFN_value(end)

'''
operation of fuzzy time
Contain function: add(X,Y);Measure(X,Y);
'''

def add(X,Y):
    return [X[_]+Y[_] for _ in range(3)]

def TFN_value(X):
    return (X[0] + 2 * X[1] + X[2]) / 4

def Measure(X,Y):
    F_X=TFN_value(X)
    F_Y=TFN_value(Y)
    if F_X!=F_Y:
        if F_X>F_Y:return True
        else:return False
    else:
        if X[1]!=Y[1]:
            if X[1]>Y[1]:return True
            else:return False
        else:
            if X[2]-X[0]>Y[2]-Y[0]:return True
            else:return False