关于数据均衡化方法的简介（以EasyEnsemble算法为例）

Posted 2022-10-29 卖山楂啦prss

1 数据均衡方法

数据的不均衡问题往往会让模型更偏向于多数类的样本，而对少数类样本的识别表现不佳，因此数据的不均衡是模型构建中需要重点解决的问题。

常用的解决方法可以划分为两个层面：

• 一个层面是从数据的角度出发，通过采样的方式调整样本类别比例来实现数据的均衡；
• 另外一个层面是从算法的角度考虑，通过集成的思想改进算法或者构建新的分类算法来实现数据的均衡。

（1）数据层面

对于数据层面而言，通过采样来实现数据的均衡化是非常简单有效的一种方式，常用的采样方法包括欠采样、过采样以及组合采样等。具体的：

1）欠采样也称为下采样（Under-Sampling），是通过减少多数类样本的数量来实现数据类别的均衡。常见的欠采样方法包括：随机欠采样、Tomek Link等。其中，随机欠采样（Random Under Sampling ,RUS）的基本思想是按照少数类样本的数目，在多数类样本中随机抽取样本来使得各类别样本数达到平衡的一种方法。显然，RUS方法因具有很强的随机性，极可能会造成多数类样本中重要信息的丢失，导致模型对样本分类的准确率降低，出现欠拟合。

2）过采样也称为上采样（Over-Samplig），，是通过增大少数类样本的数量来实现数据类别的均衡。常用的过采样方法是随机过采样、SMOTE过采样等。对于随机过采样（Random OverSampling,ROS），其基本思想是对少数类样本不断进行随机抽样，直到达到与多数类样本数量一致才停止，可以看出这种方法在平衡数据集时并没有新的数据信息的加入，不断重复增加少数类样本信息将非常容易出现过拟合现象。如下图所示，分别展示了欠采样方法和过采样方法的前后数据量过程。

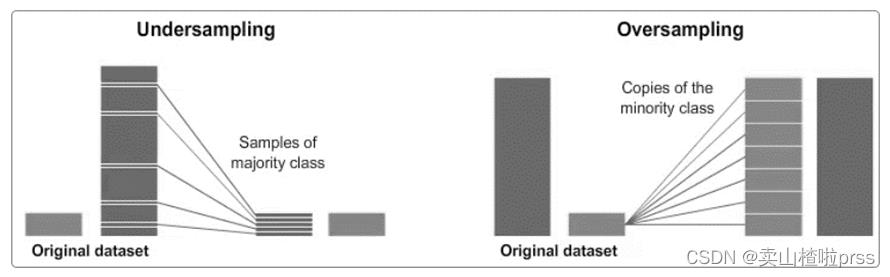
为解决随机过采样会导致模型过拟合的问题，后续又提出SMOTE算法。该方法基于线性插值的思想，利用KNN技术来生成新的少数类样本，这种该方法相比ROS有很大的改进，可以有效的避免模型过拟合，但是当少数类样本和多数类样本的边界模糊时，这种方法生成新少数类样本会将没有价值，反而使得模型效果降低。

因此，为弥补过采样方法的不足，随后学者们又基于SMOTE过采样提出了如SMOTETomek、BorderlineSMOTE以及STMOTEENN等改进采样方法。

（2）算法层面

（1）集成学习是处理不均衡数据常用的方法之一，其基本思想是通过一种分而治之的策略将多个分类器集合起来，再根据一定的规则得到最终结果，从而解决共同的问题。根据目前的研究文献[26]表明，集成学习方法对研究不均衡数据有较好的效果。目前，常见包括SMOTEBagging、UnderOverBagging等算法。

（2）代价敏感法主要通过在训练函数中对不同类别的样本给予不同的错分代价，从而实现解决不均衡数据的问题。通过设置不同的代价，模型会对样本给予不同的重视程度，区别对待多数类和少数类，提高错分少数类的代价。

2 EasyEnsemble算法

对于数据的不均衡问题，欠采样是最简单有效的一种方法，当数据为大量级且处于轻度或中度不均衡时，使用欠采样方法通常要优于其他采样方法，不过欠采样方法也存在明显不足，即极有可能造成数据信息的损失。

为此，2006年X.Y.Liu和J.Wu等人提出了一种基于欠采样技术与集成学习技术相结合的EasyEnsemble算法，该算法针对欠采样可能会损失重要信息的不足作了一定的改进，即按照少数类样本的数量将多数类样本分割成多个子集，然后分别与少数类样本进行组合，之后将各个组合样本分别使用Adaboost算法进行训练，最终通过集成策略输出结果。

具体的，EasyEnsemble算法的基本流程如下表所示：

可以看出，该算法本质上还是一种欠采样技术，虽然欠采样后每个组合子集中多数类样本数量不及多数类样本总数量，但是在无放回的随机采样情况下将所有多数类样本子集组合起来仍然是多数类样本全集，从全局来看并没有丢失有效信息，所以这是一种简单且高效的数据不均衡处理方法。

参考文献：
基于E-LightGBM算法的5G套餐潜在客户识别研究[D],2022