最优化所需基础知识-第二节：凸集

Posted 2022-10-28 快乐江湖

• B

文章目录

• 一：直线和线段
• 二：仿射集
• （1）仿射集定义
• （2）仿射组合
• （3）仿射集的子空间
• （4）仿射包
• 二：凸集
• （1）凸集定义
• （2）凸集的性质
• （3）凸组合
• （4）凸包
• （5）锥、锥组合和凸锥

一：直线和线段

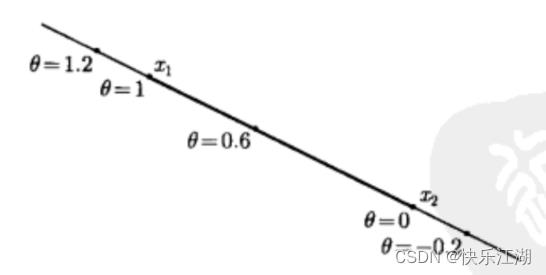
直线：设$x_1$和$x_2$为$\\R^n$空间中两个不同的点，那么经过这两个点可以确定一条直线

$$y=\\theta x_1+(1-\\theta)x_2,\\theta\\in \\R$$

关于上式可以这样理解，首先将其变形为$y=x_2+\\theta(x_1-x_2),\\theta\\in \\R$

• $\\theta(x_1-x_2)$表示方向由$x_2$到$x_1$，大小由$\\theta$控制，则$y$表示基点$x_2$和它们的和
• 当$\\theta=0$时，$y$就在$x_2$处；当$\\theta=1$时，$y$就在$x_1$处
• 所以当$0 \\leq \\theta \\leq1$时，直线就退化为以$x_1$和$x_2$为端点的线段

二：仿射集

（1）仿射集定义

仿射集：如果过集合$C$中任意两点的直线都在$C$内，那么称集合$C$是仿射的，也即$C$为仿射集。由于前面已经给出了直线的表达式，所以这里可以等价描述为：对于任意的$x_1,x_2\\in C$及$\\theta \\in R$，都有$\\theta x_1+(1-\\theta)x_2\\in C$，也即

$$x_1,x_2\\in C =>\\theta x_1+(1-\\theta)x_2\\in C,\\forall\\theta\\in \\R$$

换言之：$C$包含了$C$中任意两点的系数之和为1的线性组合

• 例如：线性方程组$Ax=b$的解集$\\chi$是仿射集，因为$\\forall x_1,x_2\\in \\chi(x_1\\not=x_2)$均满足$\\theta Ax_1+(1-\\theta)Ax_2=b$。反之，任何仿射集均可以表示为某一线性方程组的解集

（2）仿射组合

• （1）中仿射集的定义只是针对两个点，其实这个定义可以推广至多个点

仿射组合：如果$\\theta_1+\\theta_2+...+\\theta_k=1$，则称$\\theta_1x_1+\\theta_2x_2+...+\\theta_kx_k$形式的点为$x_1, x_2, ... , x_k$的仿射组合。所以，一个仿射集包含任意点的仿射组合，也即若$C$是一个仿射集合，有$x_1, x_2, ... , x_k\\in C$且$\\theta_1+\\theta_2+...+\\theta_k=1$