多径信道下通过LMS均衡算法提高通信质量

Posted 2022-10-26 fpga和matlab

目录

一、理论基础

二、核心程序

三、仿真测试结果

---

作者ID  ：fpga和matlab
CSDN主页：https://blog.csdn.net/ccsss22?type=blog
擅长技术：
1.无线基带,无线图传,编解码 
2.机器视觉,图像处理,三维重建 
3.人工智能,深度学习 
4.智能控制,智能优化
5.其他

一、理论基础

        在无线通信系统中，信道特性的变化对通信质量有着重要的影响。对通信信道的自适应均衡是无线通信中的一个重要问题。通过信道自适应均衡可以在信道特性发生变化后快速适应至正常通信。本课题主要研究由滑动自回归系统构成的信道均衡模型。由于LMS算法具有结构简单，运行速度快的优点。本本课题使用LMS算法在滑动自回归系统上实现信道自适应均衡，验证了LMS算法在二阶条件下的收敛过程以及在QPSK调制模型的自适应均衡結果。通过验证可以得出LMS算法在信道自适应均衡过程中可以得到较好的结果。

       自适应均衡属于自适应信号处理的应用范畴，各种各样的自适应均衡算法如迫零（ZF）算法、最小均方（LMS）算法、递归最小二乘（RLS）算法、变换域均衡算法、Bussgang 算法、高阶或循环统计量算法、基于非线性滤波器或神经网络的均衡算法等应运而生。均衡器通常工作在接收机的基带或中频信号部分，基带信号的复包络含有信道带宽信号的全部信息，所以，均衡器通常在基带信号完成估计信道冲激响应和解调输出信号中实现自适应算法等，本文选择了两种典型的自适应算法：以LMS自适应均衡器和RLS自适应均衡器为基础，用MATLAB 仿真软件对LMS和RLS两种算法进行仿真，比较并分析了两种算法的性能。

       LMS算法有它自身的优点，但是，由于LMS算法采用梯度矢量的瞬时估计，有大的方差，以至于不能获得最优滤波性能。

二、核心程序

clc;
clear;
close all;
warning off;
addpath 'func\\'

%**************************************************************************
%**************************************************************************
%********(0)整个算法的流程如下所示：
%********(1)产生信号
%********(2)QPSK调制
%********(3)信道，加入多径信号
%********(4)QPSK解调
%********(5)LMS均衡
%********(6)判决
%********(7)得到误码率，眼图，星座图
%**************************************************************************
%**************************************************************************

Symble_Rate       = 1e6;                          %符号速率
Sample_Frequency  = 32e6;                         %时钟采样率
Frequency_carrier = 512e6;                        %初始载波频率
Number            = 40000;                        %仿真bit符号数    
SNR               = 0:1:12;
alpha             = 0.5;                          %成形滤波和匹配滤波器的滚降系数
Delay             = [0 20 50]/Sample_Frequency; %设置多径延迟
Gain              = [0 -4 -8];                      %设置每一径的衰减
Lms_Coff1         = 0.99;
Delta             = 0.001;
Iter              = 400;

%步骤一：产生二进制信号
Signal            = double(rand(1,Number) >= 0.5);

%步骤二：产生QPSK映射信号
QPSK_signal       = func_QPSK_map(Signal,Number);

%步骤三：进行成形滤波，乘以载波进行QPSK的调制,DAC为最后发送端发送的中频信号
DAC               = func_QPSK_Modulate(QPSK_signal,Sample_Frequency,Symble_Rate,Frequency_carrier,alpha);


%开始循环，对不同的SNR下的误码率进行仿真

for i = 1:length(SNR)
    
    i
    
    %步骤四：通过多径信道       
    ADC          = func_multipath(DAC,Sample_Frequency,Delay,Gain,SNR(i),Symble_Rate);

    %步骤五：数字下变频
    I_Q          = func_QPSK_DeModulate(ADC,Sample_Frequency,Frequency_carrier,Symble_Rate,alpha);

    %步骤六：LMS均衡算法 
    [Data,Learn] = func_LMS_eq(QPSK_signal,Number,I_Q,Lms_Coff1,Delta,Iter);

    %步骤七：判决        
    R            = func_check(Data,Number);


    %步骤八：计算误码率误码率
    error         = find(Signal(2*Iter+1:end)-R(2*Iter+1:end));
    error_sum     = length(error);
    error_rate(i) = error_sum/length(Signal(2*Iter+1:end));


    %步骤九：绘制中间图
    figure(1);
    plot(real(QPSK_signal),imag(QPSK_signal),'r*');   
    title('发送端：QPSK映射星座图') 

    figure(2);
    plot(DAC);
    title('上变频：QPSK映射星座图') 

    figure(3);
    plot(ADC);
    title('多径信道：QPSK映射星座图') 

    figure(4);
    plot(I_Q);   
    title('下变频后：QPSK映射星座图')

    figure(5);
    plot(Data);  
    title('LMS均衡后：QPSK映射星座图')
end


figure(6);
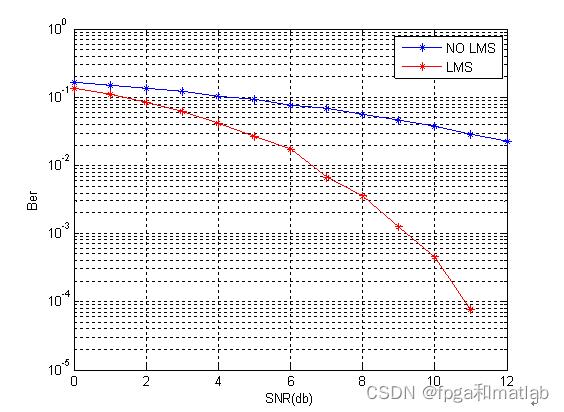
semilogy(SNR,error_rate,'b-*');
grid on
xlabel('SNR(db)');
ylabel('Ber');

figure(7);

subplot(211);
s = real(Data);
L = floor(length(s)/200);

for jj=1:200
    plot(s((jj-1)*L+1:(jj-1)*L+L));
    hold on;
end 

subplot(212); 
s = imag(Data);
L = floor(length(s)/200);

for jj=1:200
    plot(s((jj-1)*L+1:(jj-1)*L+L));
    hold on;
end 


figure(8);
subplot(211);
plot(real(I_Q(2000:2400)));
subplot(212); 
plot(real(Data(2000:2400)));

figure(9);
plot(abs(Learn(11:end)));

save lms.mat SNR error_rate

三、仿真测试结果

本课题仿真所涉及到的仿真参数如下所示：

参数	含义	值
Symble_Rate	符号速率	1M
Sample_Frequency	时钟采样速率	32M
Frequency_carrier	载波频率	512M
Number	仿真bit个数	40000
SNR	SNR	0,1,2,3,4,5,6,7,8,9,10,11,12
alpha	滤波器滚降系数	0.5
Delay	多径延迟	20,50
Gain	多径增益	-4，-8
Lms_Coff1	LMS算法系数1	0.99
Delta	LMS算法系数2	0.001
Iter	LMS迭代次数	400

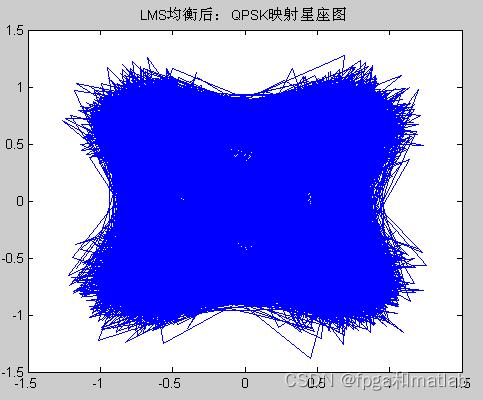
QPSKLMS均衡后输出

    图1的仿真结果是各个仿真过程中的星座图，从上面的仿真结果可知，通过多径信道之后，系统的星座图明显恶化，在通过LMS均衡之后，系统的星座图得到改善。

   从图3的仿真结果可知，通过LMS均衡之后，系统的符号信息得到明显的改善。

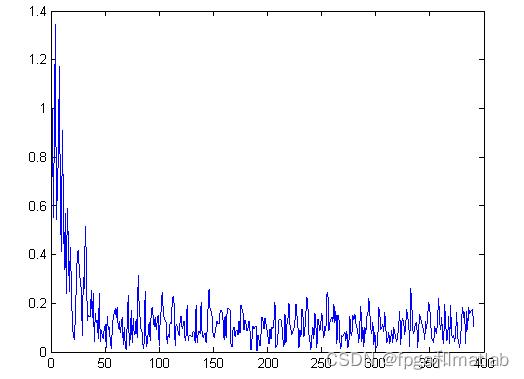
图5 LMS算法收敛曲线

   图5为LMS均衡算法的收敛曲线。

 A25-06