PRML 学习: Polynomial Curve Fitting

Posted 2022-10-25 yhl_leo

本系列文章由 @YhL_Leo 出品，转载请注明出处。 文章链接： http://blog.csdn.net/yhl_leo/article/details/75534111

---

多项式曲线拟合是比较基础的回归分析方法，假设有一独立变量 $x$ 和与其相关的变量 $y$，存在着变量 $x$ 的 $m$ 阶多项式可以模拟这种映射关系，可以用于解决一些非线性拟合问题。

1 基础概念

给定一组包含 $n$ 个观测数据 $x$，$\mathbf{x}=x_0,x_1,\dots ,x_n$，和其对应的预测值 $y$, $\mathbf{y}=y_0,y_1,\dots ,y_n$, 例如图1中利用 $sin(2\pi x)$ 函数合成的观测数据（30组加入了随机均匀噪声的观测值）。我们的目标就是使用这样的一个观测数据，训练/学习到一个模型，当引入新的数值 $\hat{x}$ 时，可以有效得预测它对应的数值 $\hat{y}$ 。

图 1

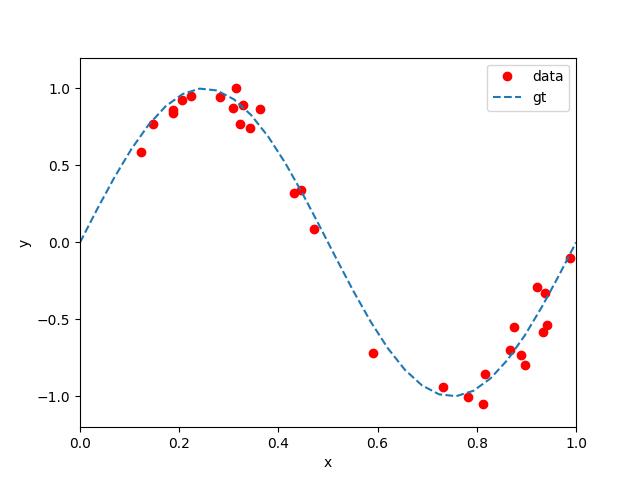
可以看出，实现这一目标暗示着，我们要尽可能地找到观测数据所对应的潜在的模型，即 $sin(2\pi x)$ 。 但是要通过有限的观测数据（含有噪声）准确地泛化出这一模型，是相当困难的。即便如此，我们还是可以把这一问题简化成为曲线拟合问题。我们指定采用的多项式形式为：

$$y(x,\mathbf{w})=w_0+w_{1}x+w_2\ast x^2+\cdots +w_m{x}^m=\sum _{i=0}^m{w}_i{x}^i,\text{\hspace{1em}(1)}$$

其中，取 $x$ 幂次最高值 $m$， 称该多项式为 $m$ 次多项式。虽然，该多项式是 $x$ 的非线性函数，但是却是待系数 $\mathbf{w}$ 的线性方程。方程$(1)$ 的矩阵形式为：
$$\mathcal{Y}\text{Y}\mathcal{Y}=\mathcal{X}\text{X}\mathcal{X}\mathbf{w},\text{\hspace{1em}(2)}$$

其中，
$$\mathcal{Y}\text{Y}\mathcal{Y}=\left[\begin{array}{c}{y}_0\\ y_1\\ ⋮\\ y_n\end{array}\right],$$

$$\mathcal{X}\text{X}\mathcal{X}=\left[\begin{array}{cccc}1& x_0& x_0^2\dots & x_0^m\\ 1& x_1& x_1^2\dots & x_1^m\\ & & ⋮& \\ 1& x_n& x_n^2\dots & x_n^m\end{array}\right],$$

$$\mathbf{w}=\left[\begin{array}{c}{w}_0\\ w_1\\ ⋮\\ w_n\end{array}\right]$$

通过观测数据就可以确定该多项式的系数，假设我们已经得到了这样一组系数