从Non-negative Matrix Factorization说说Clustering

Posted 2022-10-17 vast_w

转载：http://maider.blog.sohu.com/303848412.html

背景：

假设你在Netflix工作，拿到了一个matrix形式的dataset： 1    2    1   ...   5    0 3    4    0   ...   1    1 ...             5    2    1   ...   3    2
这个dataset包含了m个用户对n部电影的rating（rating在0-5之间），故这个matrix的大小为n*m。每一个column表示单个用户对n部电影的rating情况，例如示例矩阵中用户1对第一部电影的评分是1，对第二部电影的评分是3， 对第n部电影的评分是5。我们假设表示dataset的matrix为

V

。

Matrix Factorization：

如果我们能找到两个矩阵：

W

（大小为n*r），

H

（大小为r*m），并且

V

=

WH

，那么我们就相当于将这个dataset聚为了r个类。

W

可以看作r列长度为n的向量组成的矩阵，每个向量表示一个类的基向量(basis vector)，

W其实就是个存放r个类的基向量的矩阵

。而

H

则可以看成m列长度为r的向量组成的矩阵，每个向量表示

V

中的每个数据（即V中的每一列）软分配（soft label）到各个类中的权重。如果用小写的v表示

V

中的每一列，用小写的h表示

H

中的每一列，则v=

W

h。
如果我们允许

W

中包含任意值（正、负均可），那么

V

=

WH

就是个普通的Matrix Factorization。虽然可以用于聚类，但是结果却不够直观： 1. 用户的rating只可能是0，1，2，3，4，5，如果

W

里含有负值，相当于表示某个类的基向量给出了负分的评价。（这是Netflix而不是留几手，不能负分滚粗的哦，亲） 2. 在soft label时，我们常常这么表示一个数据的聚类结果：这个data point有30%的可能来自类1，有20%的可能来自类2，有50%的可能来自类3。。。 如果

H

里含有负值，就无法理解为何一个data point有 负百分之几的可能性来自某个类。
参考资料： http://www.quuxlabs.com/blog/2010/09/matrix-factorization-a-simple-tutorial-and-implementation-in-python/

Non-negative Matrix Factorization

于是，我们就想对W和H都加以限制，让它们中的每一个元素都为非负值，这就是所谓的Nonnegative Matrix Factorization，更正式的定义则为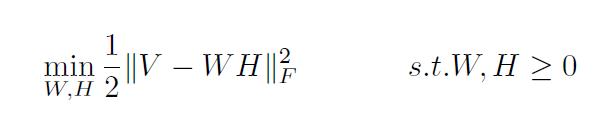： norm号带下标F意为Frobenius Norm： http://mathworld.wolfram.com/FrobeniusNorm.html
那么如何解出

W

和

H

呢？首先，先随机初始化

W

和

H

；之后，用gradient descent的方法，不断迭代更新W和H直至稳定。（Gradient Descent迭代的方法，以及最终W和H会Converge的证明，参见： http://hebb.mit.edu/people/seung/papers/nmfconverge.pdf）

Non-negative Matrix Factorization 和K-means的关系

不敢越俎代庖，Gatech的一个韩国棒子在这篇paper里解释了Non-negative Matrix Factorization和K-means的关系， http://www.cc.gatech.edu/~hpark/papers/GT-CSE-08-01.pdf。我在这里只说说本人自己intuitive的解释： Kmeans中的

W

同样是 存放r个类的基向量的矩阵，只不过每个基向量必须是那个类的中心（centroid），Kmeans中的H同样表示各个数据点分配到各个类的权重，只不过H的每一列只有一个非0元素（即每个数据点被hard label到唯一的一个类）。而Non-negative Matrix Factorization则放宽了这些要求，W中的每一列向量虽为每个类的basis vector，但不必是centroid；H中的每一列向量并不只能有一个非0的元素，即NMF为soft label形式的聚类算法。

Sparse Non-negative Matrix Factorization——游走于K-means和NMF之间

我们不想让如果每个数据点只属于一个类，但也不想让每个数据点由太多类“组成”，那么我们就要加一个regularization的系数，来让

H

尽可能的sparse：

H

中的每一列由尽可能少的非0元素构成。SNMF的构成，即迭代方法，在韩国棒子的那篇paper里也有。

如何定义聚类的个数？

K-means和NMF共同遇到的问题就是需要事先人为定下聚类的个数。韩国棒子的那篇paper，还讲到了一个算法（dispersion coeffient），来大致决定聚类的个数。但我想说的是，在不事先知道dataset的类的数目的时候，有一种更diao的方法，那就是Dirichlet Mixture Model：  http://blog.echen.me/2012/03/20/infinite-mixture-models-with-nonparametric-bayes-and-the-dirichlet-process/，大致的思路是在遍历每一个data point的时候，这个data point会以概率Pn被分配到已经存在的第n个cluster，概率Pn和第n个cluster中已有的数据个数成正比，或者以概率Pnew分配到新的cluster中，概率Pnew随着已聚好类的data point个数的增加而减少。

还有哪些聚类的方法？

除了Kmeans和NMF，常见的聚类方法还有Archetypal Analysis、Principle Component Analysis以及Hierarchical Clustering。NEU Game Department的一位教授（虽然这位教授已经远走Denmark只在NEU挂名），通过常见的这几种聚类方法，对World of Warcraft 7万多名玩家的升级数据进行聚类，并对比了它们各自的优缺点： https://www.dropbox.com/s/x9r2f3zq0i9ym7n/A%20Comparison%20of%20Methods%20for%20Player%20Clustering%20via%20Behavioral%20Telemetry.pdf 从结果显示，K means在实际应用中，易产生多个非常相似的centroid，使得我们不容易区分每一个类的特征。NMF和PCA产生的basis vector虽然理论上正确，但却不符合实际情况（例如在这篇文章中，某个类的基向量表示玩家的level随着时间的增加竟然可以减少），所以也不利于我们分析出各个类的特征。而Archetypal Analysis产生的结果最利于直观分析。