循环神经网络及其变体深度解读
Posted 彭祥.
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了循环神经网络及其变体深度解读相关的知识,希望对你有一定的参考价值。
RNN存在梯度消失和梯度爆炸的问题,因此提出了LSTM等变体来解决这个问题,针对RNN的问题,是如何解决的呢?
LSTM如何改进RNN
其实,长短时记忆网络的思路比较简单。原始RNN的隐藏层只有一个状态,即h,它对于短期的输入非常敏感。那么,假如我们再增加一个状态,即c,让它来保存长期的状态,那么问题不就解决了么?如下图所示:
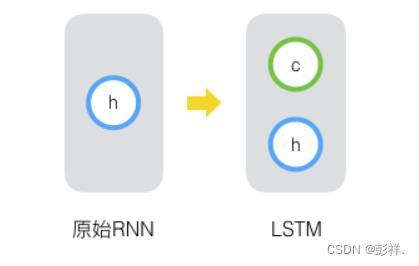
新增加的状态c,称为单元状态(cell state)。我们把上图按照时间维度展开:
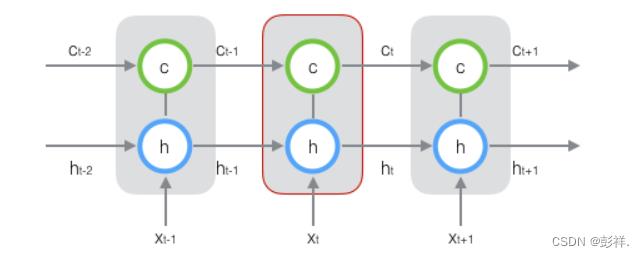
上图仅仅是一个示意图,我们可以看出,在t时刻,LSTM的输入有三个:当前时刻网络的输入值x t 、上一时刻LSTM的输出值 h t−1 、以及上一时刻的单元状态c t−1 ;LSTM的输出有两个:当前时刻LSTM输出值h t 、和当前时刻的单元状态ct。注意 x t 、 h t 、 ct 都是向量。
LSTM的关键,就是怎样控制长期状态c 。在这里,LSTM的思路是使用三个控制开关。第一个开关,负责控制继续保存长期状态c;第二个开关,负责控制把即时状态输入到长期状态c ;第三个开关,负责控制是否把长期状态c作为当前的LSTM的输出。三个开关的作用如下图所示:
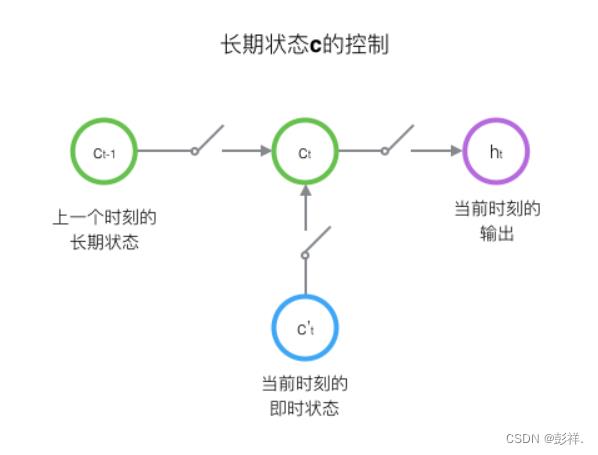
接下来,我们要描述一下,输出h和单元状态c的具体计算方法。
长短时记忆网络的前向计算
前面描述的开关是怎样在算法中实现的呢?这就用到了门(gate)的概念。门实际上就是一层全连接层,它的输入是一个向量,输出是一个0到1之间的实数向量。假设W是门的权重向量,b 是偏置项,那么门可以表示为:
g(x)=σ(Wx+b)
门的使用,就是用门的输出向量按元素乘以我们需要控制的那个向量。因为门的输出是0到1之间的实数向量,那么,当门输出为0时,任何向量与之相乘都会得到0向量,这就相当于啥都不能通过;输出为1时,任何向量与之相乘都不会有任何改变,这就相当于啥都可以通过。因为σ (也就是sigmoid函数)的值域是(0,1),所以门的状态都是半开半闭的。
LSTM用两个门来控制单元状态c 的内容,一个是遗忘门(forget gate),它决定了上一时刻的单元状态ct−1有多少保留到当前时刻ct;另一个是输入门(input gate),它决定了当前时刻网络的输入x t 有多少保存到单元状态c t 。LSTM用输出门(output gate)来控制单元状态c t 有多少输出到LSTM的当前输出值ht。
我们先来看一下遗忘门:
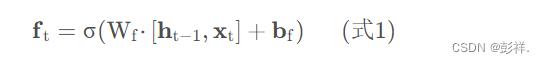
上式中,W f 是遗忘门的权重矩阵,[ h t−1 , x t ],表示把两个向量连接成一个更长的向量,b f 是遗忘门的偏置项,σ 是sigmoid函数。如果输入的维度是d x ,隐藏层的维度是d h,单元状态的维度是d c (通常d c = d h ),则遗忘门的权重矩阵W f 维度是d c × ( d h + d x ) 。事实上,权重矩阵Wf 都是两个矩阵拼接而成的:一个是W fh ,它对应着输入项h t−1 ,其维度为d c × d h ;一个是W fx ,它对应着输入项x t ,其维度为d c× d x 。W f 可以写为:
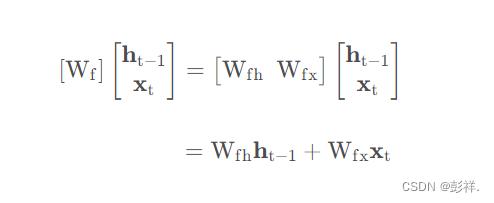
下图显示了遗忘门的计算:
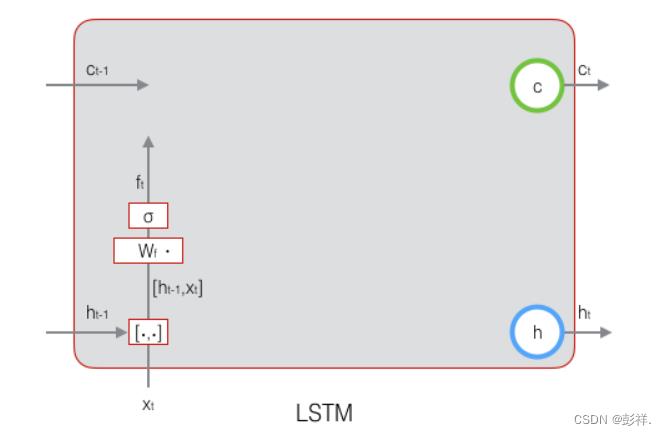
接下来看看输入门:
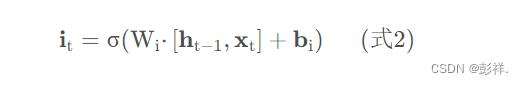
上式中,W i 是输入门的权重矩阵,b i 是输入门的偏置项。下图表示了输入门的计算:
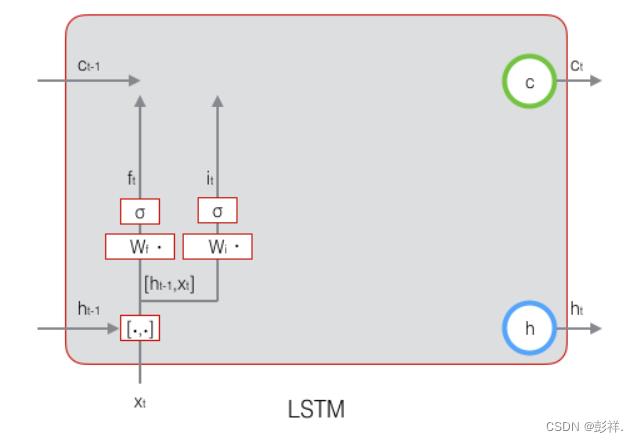
接下来,我们计算用于描述当前输入的单元状态c t ,它是根据上一次的输出和本次输入来计算的:
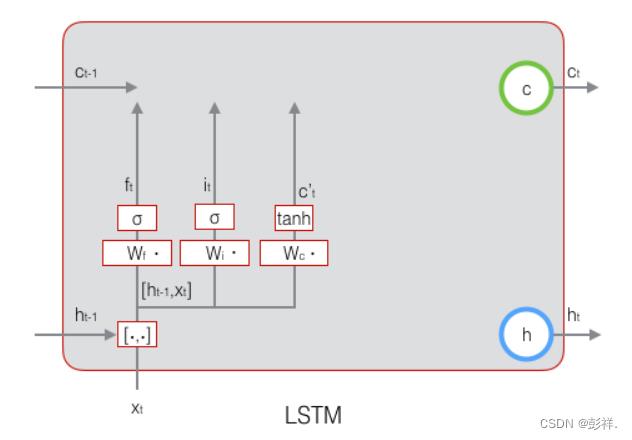
现在,我们计算当前时刻的单元状态c t。它是由上一次的单元状态c t−1 按元素乘以遗忘门f t,再用当前输入的单元状态c t 按元素乘以输入门i t,再将两个积加和产生的:

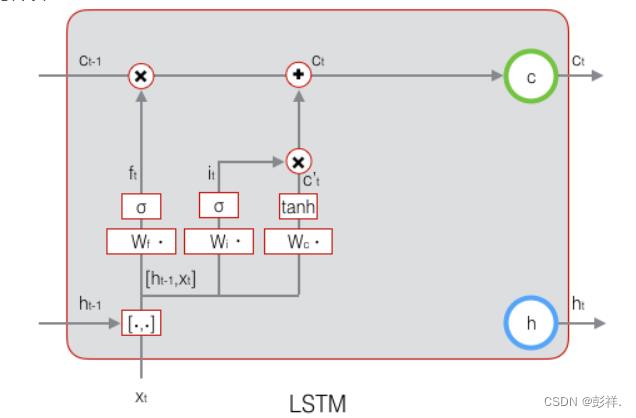
这样,我们就把LSTM关于当前的记忆c t和长期的记忆ct−1组合在一起,形成了新的单元状态c t 。由于遗忘门的控制,它可以保存很久很久之前的信息,由于输入门的控制,它又可以避免当前无关紧要的内容进入记忆。下面,我们要看看输出门,它控制了长期记忆对当前输出的影响:
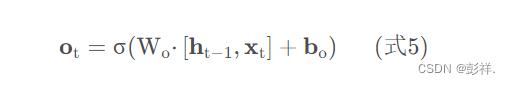
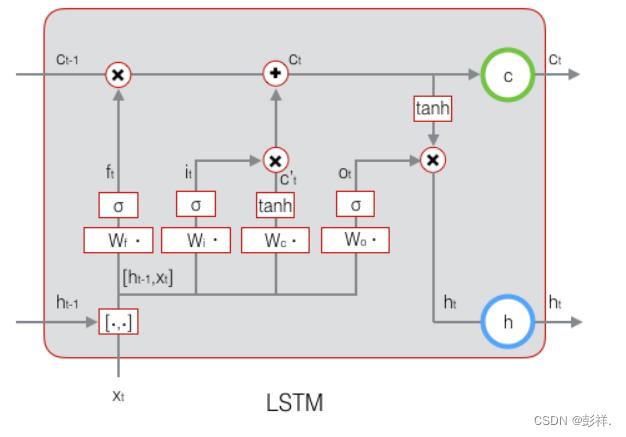
下图表示输出门的计算:
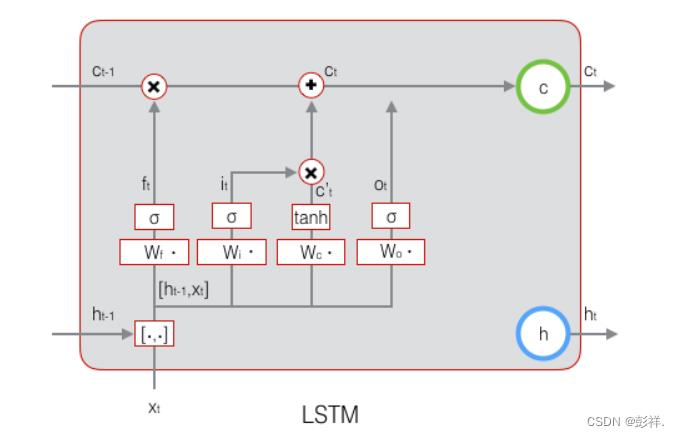
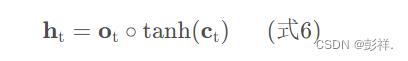
下图表示LSTM最终输出的计算:
(式1)到(式6)就是LSTM前向计算的全部公式。至此,我们就把LSTM前向计算讲完了。
长短时记忆网络的训练
训练部分往往比前向计算部分复杂多了。LSTM的前向计算都这么复杂,那么,可想而知,它的训练算法一定是非常非常复杂的。
LSTM训练算法框架
LSTM的训练算法仍然是反向传播算法,对于这个算法,我们已经非常熟悉了。主要有下面三个步骤:
- 1.前向计算每个神经元的输出值,对于LSTM来说,即f t 、 i t 、 c t 、 o t 、 h t五个向量的值。计算方法已经在上一节中描述过了。
- 2.反向计算每个神经元的误差项δ 值。与循环神经网络一样,LSTM误差项的反向传播也是包括两个方向:一个是沿时间的反向传播,即从当前t时刻开始,计算每个时刻的误差项;一个是将误差项向上一层传播。
- 3.根据相应的误差项,计算每个权重的梯度。
-关于公式和符号的说明
首先,我们对推导中用到的一些公式、符号做一下必要的说明。
接下来的推导中,我们设定gate的激活函数为sigmoid函数,输出的激活函数为tanh函数。他们的导数分别为:

从上面可以看出,sigmoid和tanh函数的导数都是原函数的函数。这样,我们一旦计算原函数的值,就可以用它来计算出导数的值。
代码实现
而这两个函数的实现即为分为前向和反向,反向传播即为其导数
class SigmoidActivator(object):
def forward(self, weighted_input):
return 1.0 / (1.0 + np.exp(-weighted_input))
def backward(self, output):
return output * (1 - output)
class TanhActivator(object):
def forward(self, weighted_input):
return 2.0 / (1.0 + np.exp(-2 * weighted_input)) - 1.0
def backward(self, output):
return 1 - output * output
我们把LSTM的实现放在LstmLayer类中。
在构造函数的初始化中,只初始化了与forward计算相关的变量,与backward相关的变量没有初始化。这是因为构造LSTM对象的时候,我们还不知道它未来是用于训练(既有forward又有backward)还是推理(只有forward)。
class LstmLayer(object):
def __init__(self, input_width, state_width,
learning_rate):
self.input_width = input_width
self.state_width = state_width
self.learning_rate = learning_rate
# 门的激活函数
self.gate_activator = SigmoidActivator()
# 输出的激活函数
self.output_activator = TanhActivator()
# 当前时刻初始化为t0
self.times = 0
# 各个时刻的单元状态向量c
self.c_list = self.init_state_vec()
# 各个时刻的输出向量h
self.h_list = self.init_state_vec()
# 各个时刻的遗忘门f
self.f_list = self.init_state_vec()
# 各个时刻的输入门i
self.i_list = self.init_state_vec()
# 各个时刻的输出门o
self.o_list = self.init_state_vec()
# 各个时刻的即时状态c~
self.ct_list = self.init_state_vec()
# 遗忘门权重矩阵Wfh, Wfx, 偏置项bf
self.Wfh, self.Wfx, self.bf = (
self.init_weight_mat())
# 输入门权重矩阵Wfh, Wfx, 偏置项bf
self.Wih, self.Wix, self.bi = (
self.init_weight_mat())
# 输出门权重矩阵Wfh, Wfx, 偏置项bf
self.Woh, self.Wox, self.bo = (
self.init_weight_mat())
# 单元状态权重矩阵Wfh, Wfx, 偏置项bf
self.Wch, self.Wcx, self.bc = (
self.init_weight_mat())
def init_state_vec(self):
'''
初始化保存状态的向量
'''
state_vec_list = []
state_vec_list.append(np.zeros(
(self.state_width, 1)))
return state_vec_list
def init_weight_mat(self):
'''
初始化权重矩阵
'''
Wh = np.random.uniform(-1e-4, 1e-4,
(self.state_width, self.state_width))
Wx = np.random.uniform(-1e-4, 1e-4,
(self.state_width, self.input_width))
b = np.zeros((self.state_width, 1))
return Wh, Wx, b
前向计算的实现
forward方法实现了LSTM的前向计算:
def forward(self, x):
'''
根据式1-式6进行前向计算
'''
self.times += 1
# 遗忘门
fg = self.calc_gate(x, self.Wfx, self.Wfh,
self.bf, self.gate_activator)
self.f_list.append(fg)
# 输入门
ig = self.calc_gate(x, self.Wix, self.Wih,
self.bi, self.gate_activator)
self.i_list.append(ig)
# 输出门
og = self.calc_gate(x, self.Wox, self.Woh,
self.bo, self.gate_activator)
self.o_list.append(og)
# 即时状态
ct = self.calc_gate(x, self.Wcx, self.Wch,
self.bc, self.output_activator)
self.ct_list.append(ct)
# 单元状态
c = fg * self.c_list[self.times - 1] + ig * ct
self.c_list.append(c)
# 输出
h = og * self.output_activator.forward(c)
self.h_list.append(h)
def calc_gate(self, x, Wx, Wh, b, activator):
'''
计算门
'''
h = self.h_list[self.times - 1] # 上次的LSTM输出
net = np.dot(Wh, h) + np.dot(Wx, x) + b
gate = activator.forward(net)
return gate
反向传播算法的实现
backward方法实现了LSTM的反向传播算法。需要注意的是,与backword相关的内部状态变量是在调用backward方法之后才初始化的。这种延迟初始化的一个好处是,如果LSTM只是用来推理,那么就不需要初始化这些变量,节省了很多内存。
def backward(self, x, delta_h, activator):
'''
实现LSTM训练算法
'''
self.calc_delta(delta_h, activator)
self.calc_gradient(x)
算法主要分成两个部分,一部分使计算误差项:
def calc_delta(self, delta_h, activator):
# 初始化各个时刻的误差项
self.delta_h_list = self.init_delta() # 输出误差项
self.delta_o_list = self.init_delta() # 输出门误差项
self.delta_i_list = self.init_delta() # 输入门误差项
self.delta_f_list = self.init_delta() # 遗忘门误差项
self.delta_ct_list = self.init_delta() # 即时输出误差项
# 保存从上一层传递下来的当前时刻的误差项
self.delta_h_list[-1] = delta_h
# 迭代计算每个时刻的误差项
for k in range(self.times, 0, -1):
self.calc_delta_k(k)
def init_delta(self):
'''
初始化误差项
'''
delta_list = []
for i in range(self.times + 1):
delta_list.append(np.zeros(
(self.state_width, 1)))
return delta_list
def calc_delta_k(self, k):
'''
根据k时刻的delta_h,计算k时刻的delta_f、
delta_i、delta_o、delta_ct,以及k-1时刻的delta_h
'''
# 获得k时刻前向计算的值
ig = self.i_list[k]
og = self.o_list[k]
fg = self.f_list[k]
ct = self.ct_list[k]
c = self.c_list[k]
c_prev = self.c_list[k-1]
tanh_c = self.output_activator.forward(c)
delta_k = self.delta_h_list[k]
# 根据式9计算delta_o
delta_o = (delta_k * tanh_c *
self.gate_activator.backward(og))
delta_f = (delta_k * og *
(1 - tanh_c * tanh_c) * c_prev *
self.gate_activator.backward(fg))
delta_i = (delta_k * og *
(1 - tanh_c * tanh_c) * ct *
self.gate_activator.backward(ig))
delta_ct = (delta_k * og *
(1 - tanh_c * tanh_c) * ig *
self.output_activator.backward(ct))
delta_h_prev = (
np.dot(delta_o.transpose(), self.Woh) +
np.dot(delta_i.transpose(), self.Wih) +
np.dot(delta_f.transpose(), self.Wfh) +
np.dot(delta_ct.transpose(), self.Wch)
).transpose()
# 保存全部delta值
self.delta_h_list[k-1] = delta_h_prev
self.delta_f_list[k] = delta_f
self.delta_i_list[k] = delta_i
self.delta_o_list[k] = delta_o
self.delta_ct_list[k] = delta_ct
另一部分是计算梯度:
def calc_gradient(self, x):
# 初始化遗忘门权重梯度矩阵和偏置项
self.Wfh_grad, self.Wfx_grad, self.bf_grad = (
self.init_weight_gradient_mat())
# 初始化输入门权重梯度矩阵和偏置项
self.Wih_grad, self.Wix_grad, self.bi_grad = (
self.init_weight_gradient_mat())
# 初始化输出门权重梯度矩阵和偏置项
self.Woh_grad, self.Wox_grad, self.bo_grad = (
self.init_weight_gradient_mat())
# 初始化单元状态权重梯度矩阵和偏置项
self.Wch_grad, self.Wcx_grad, self.bc_grad = (
self.init_weight_gradient_mat())
# 计算对上一次输出h的权重梯度
for t in range(self.times, 0, -1):
# 计算各个时刻的梯度
(Wfh_grad, bf_grad,
Wih_grad, bi_grad,
Woh_grad, bo_grad,
Wch_grad, bc_grad) = (
self.calc_gradient_t(t))
# 实际梯度是各时刻梯度之和
self.Wfh_grad += Wfh_grad
self.bf_grad += bf_grad
self.Wih_grad += Wih_grad
self.bi_grad += bi_grad
self.Woh_grad += Woh_grad
self.bo_grad += bo_grad
self.Wch_grad += Wch_grad
self.bc_grad += bc_grad
print '-----%d-----' % t
print Wfh_grad
print self.Wfh_grad
# 计算对本次输入x的权重梯度
xt = x.transpose()
self.Wfx_grad = np.dot(self.delta_f_list[-1], xt)
self.Wix_grad = np.dot(self.delta_i_list[-1], xt)
self.Wox_grad = np.dot(self.delta_o_list[-1], xt)
self.Wcx_grad = np.dot(self.delta_ct_list[-1], xt)
def init_weight_gradient_mat(self):
'''
初始化权重矩阵
'''
Wh_grad = np.zeros((self.state_width,
self.state_width))
Wx_grad = np.zeros((self.state_width,
self.input_width))
b_grad = np.zeros((self.state_width, 1))
return Wh_grad, Wx_grad, b_grad
def calc_gradient_t(self, t):
'''
计算每个时刻t权重的梯度
'''
h_prev = self.h_list[t-1].transpose()
Wfh_grad = np.dot(self.delta_f_list[t], h_prev)
bf_grad = self.delta_f_list[t]
Wih_grad = np.dot(self.delta_i_list[t], h_prev)
bi_grad = self.delta_f_list[t]
Woh_grad = np.dot(self.delta_o_list[t], h_prev)
bo_grad = self.delta_f_list[t]
Wch_grad = np.dot(self.delta_ct_list[t], h_prev)
bc_grad = self.delta_ct_list[t]
return Wfh_grad, bf_grad, Wih_grad, bi_grad, \\
Woh_grad, bo_grad, Wch_grad, bc_grad
梯度下降算法的实现
下面是用梯度下降算法来更新权重
def update(self):
'''
按照梯度下降,更新权重
'''
self.Wfh -= self.learning_rate * self.Whf_grad
self.Wfx -= self.learning_rate * self.Whx_grad
self.bf -= self.learning_rate * self.bf_grad
self.Wih -= self.learning_rate * self.Whi_grad
self.Wix -= self.learning_rate * self.Whi_grad
self.bi -= self.learning_rate * self.bi_grad
self.Woh -= self.learning_rate * self.Wof_grad
self.Wox -= self.learning_rate * self.Wox_grad
self.bo -= self.learning_rate * self.bo_grad
self.Wch -= self.learning_rate * self.Wcf_grad
self.Wcx -= self.learning_rate * self.Wcx_grad
self.bc -= self.learning_rate * self.bc_grad
梯度检查的实现
和RecurrentLayer一样,为了支持梯度检查,我们需要支持重置内部状态:
def reset_state(self):
# 当前时刻初始化为t0
self.times = 0
# 各个时刻的单元状态向量c
self.c_list = self.init_state_vec()
# 各个时刻的输出向量h
self.h_list = self.init_state_vec()
# 各个时刻的遗忘门f
self.f_list = self.init_state_vec()
# 各个时刻的输入门i
self.i_list = self.init_state_vec()
# 各个时刻的输出门o
self.o_list = self.init_state_vec()
# 各个时刻的即时状态c~
self.ct_list = self.init_state_vec()
最后,是梯度检查的代码:
def data_set():
x = [np.array([[1], [2], [3]]),
np.array([[2], [3], [4]])]
d = np.array([[1], [2]])
return x, d
def gradient_check():
'''
梯度检查
'''
# 设计一个误差函数,取所有节点输出项之和
error_function = lambda o: o.sum()
lstm = LstmLayer(3, 2, 1e-3)
# 计算forward值
x, d = data_set()
lstm.forward(x[0])
lstm.forward(x[1