时间序列~动态时间规整(Dynamic Time Wraping)
Posted 热爱科技的刘同学
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了时间序列~动态时间规整(Dynamic Time Wraping)相关的知识,希望对你有一定的参考价值。
时间序列-动态时间规整(Dynamic Time Wraping)
文章目录
一、解决的问题
测量两端时间序列的相似性。
在语音识别中,特别是单音节的识别中,每个人说话时间长短不同,导致时间序列长度不同。DTW算法就是将某些数据点的时间Wrap到另一个时间序列的某些数据点,以辅助计算相似性。
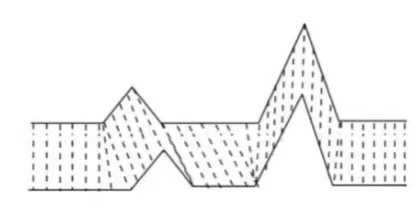
二、算法设计
1.规则
- 两端对齐
- 一个点可以对应另一序列的多个点(允许重合对应)
- 每一对数据点对齐不可交叉(只能向前对应)
2.成本矩阵
-
有两不同长度时间序列
X = x 1 , x 2 , . . . . . . , x n X=x_1,x_2,......,x_n X=x1,x2,......,xn
Y = y 1 , y 2 , . . . . . . , y m Y=y_1,y_2,......,y_m Y=y1,y2,......,ym -
构建距离矩阵
D N × M D_N×_M DN×M
矩阵元素
d i j = d i s t ( x i , y i ) d_ij=dist(x_i,y_i) dij=dist(xi,yi)
dist通常采用欧氏距离
- 在矩阵D中搜索从 d 1 1 d_11 d11到 d ( n m ) d_(nm_) d(nm)之间的最短路径(采用动态规划搜索算法,向右、上、右上三个方向搜索);
- 这个最短路径的和作为X和Y之间的相似度。
三、代码实现
'''
@Author: Classmate.Liu loved Technology
@Date: 2022-10-01 08:33:00
@LastEditTime: 2022-10-01 09:40:22
@FilePath: D:\\A\\Project_1\\main_5.py
'''
# import package
from importlib.resources import path
import numpy as np
import matplotlib.pyplot as plt
np.random.seed(42)
# define operation functions (including lambda expressions)
def DTW(X, Y, distance = lambda a, b: np.linalg.norm(a -b)):
''' dynamic time warping '''
N, M = len(X), len(Y)
cost = np.ones([N, M]) * np.inf
for i in range(N):
for j in range(M):
dist_ij = distance(X[i], Y[j])
dist_pr = min(cost[i - 1, j] if i-1>=0 else np.inf, cost[i, j-1] if j-1>=0 else np.inf, cost[i, j-1] if j-1>=0 and i+1>=0 else np.inf)
cost[i, j] = dist_ij + (dist_pr if dist_pr < np.inf else 0)
# traced back cost matrix to get minimum distance path
i, j = N - 1, M - 1
path = [(i, j)]
while i > 0 or j > 0:
condidate = []
if i-1>=0:
condidate.append((cost[i-1, j], (i-1, j)))
if j-1>=0:
condidate.append((cost[i, j-1], (i, j-1)))
if i-1>=0 or j-1>=0:
condidate.append((cost[i-1, j-1], (i-1, j-1)))
i, j = min(condidate)[1]
path.append((i, j))
return cost[N-1, M-1], path
g_X = np.random.uniform(size=18)
g_Y = np.random.uniform(size=16) + 3.0
dist, path = DTW(g_X, g_Y)
print('Dist(X, Y) = ', dist)
plt.plot(g_X)
plt.plot(g_Y)
for ij in path:
plt.plot(ij[0], ij[1]),
[g_X[ij[0]], g_Y[ij[1]], 'gray']
plt.show()
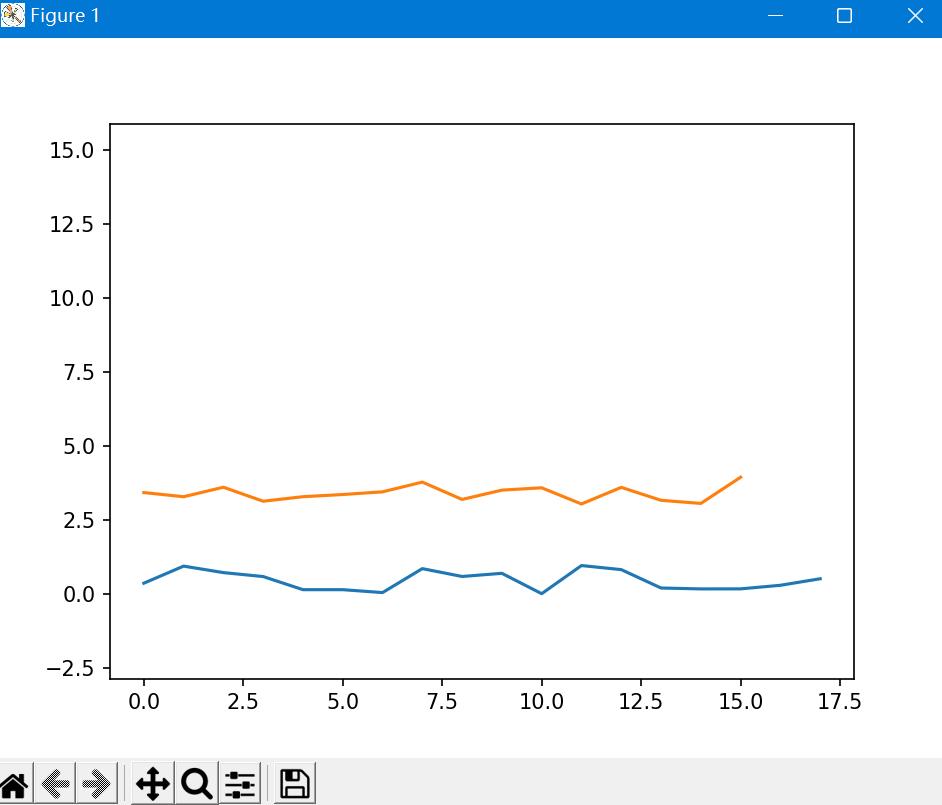
四、运行结果
图一:窗体运行结果
图二:终端运行结果

五、性能优化
- 绝大多数最短距离不会偏离对角线太远;
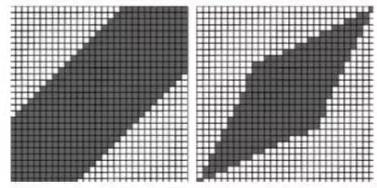
- 先在低精度下确定轮廓,随后在轮廓内计算更高精度路径。
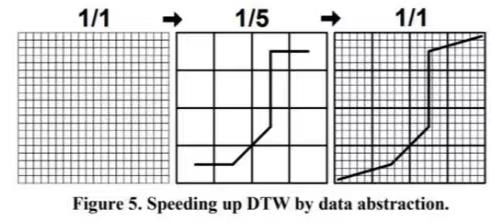
以上是关于时间序列~动态时间规整(Dynamic Time Wraping)的主要内容,如果未能解决你的问题,请参考以下文章
DTW 笔记: Dynamic Time Warping 动态时间规整 (&DTW的python实现)