树状数组。 数组修改某个元素的数值/求出前n个元素的和，需要在一百毫秒处理上百万个数字

Posted 2022-09-26 安果移不动

以16个数字来进行解释。

记住了为啥是16个。。

 

全部遍历求结果的话查询会很慢。

 

可以通过求和弄到同一个数组当中

这样可以计算就少了一半的时间

再一次

 

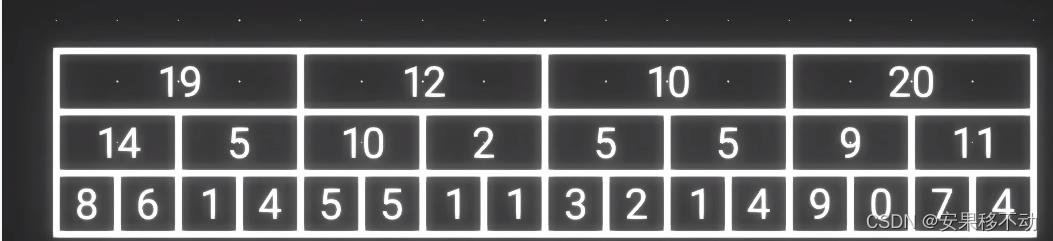
再一次

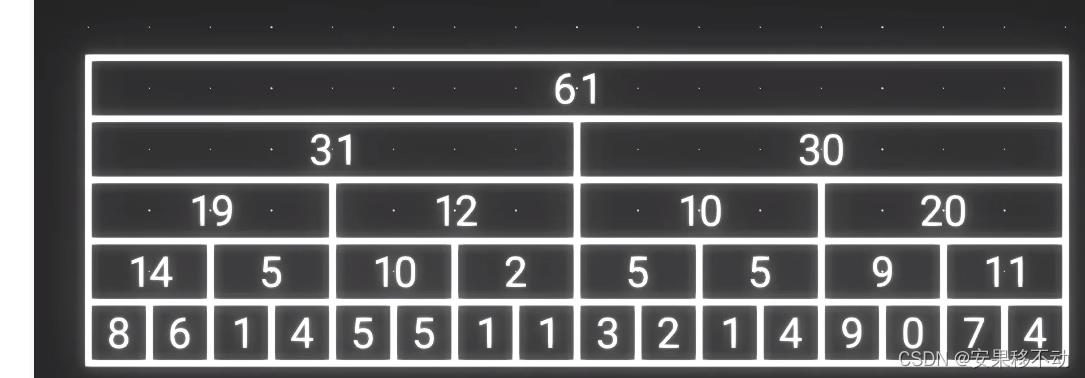
 一直这样重复。直到只剩下一个数字为止。结果不就出来了。

这样即使要求和的数字很多。我们也可以利用这些额外的数组来计算出需要的答案

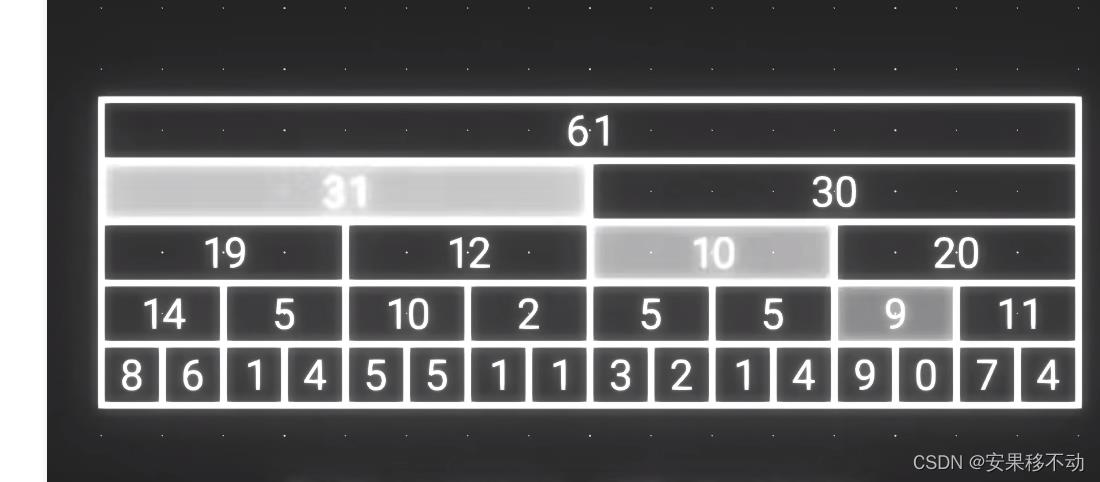
 可以看到 如果我们想计算出来前15个的累加数字

那我们实际用到的数字就 31 10 9 7 四个数字

即使要计算前一百万个数字的和，我们也只需要计算十几次 二十几次的加法。大大加快了计算速度。

上面数字有些是可以完全用不到的。。

比如我们计算前2个 前 3个 前四个 前 五个。。你会发现。

完全可以不用5

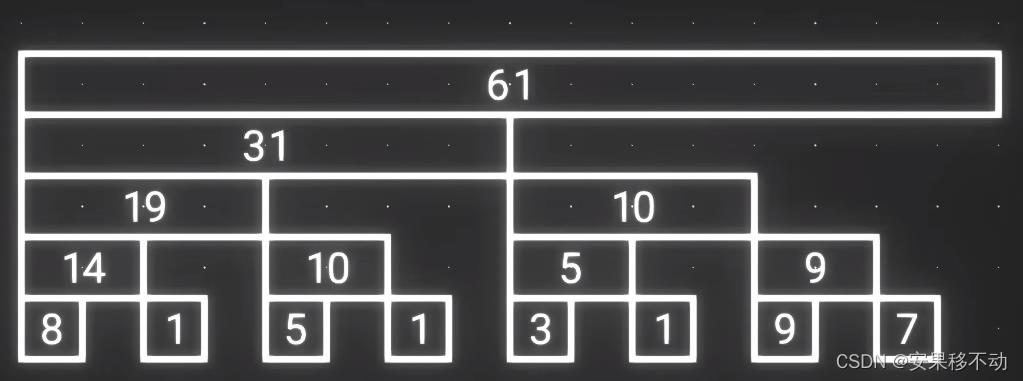
所有层数的偶数个数字都是没用的。即使去掉也没有影响。

然后观察剩下的数据。。刚好16个，我们刚才说什么16个。。。。有点。。有点巧合。。

拼接起来

 组合方式也是有规律的哦

 

 

 

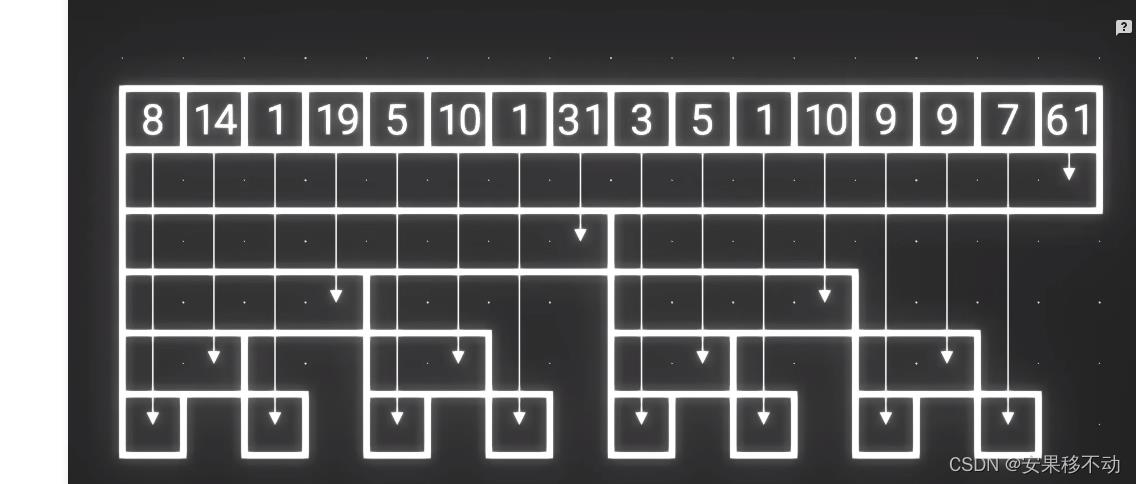
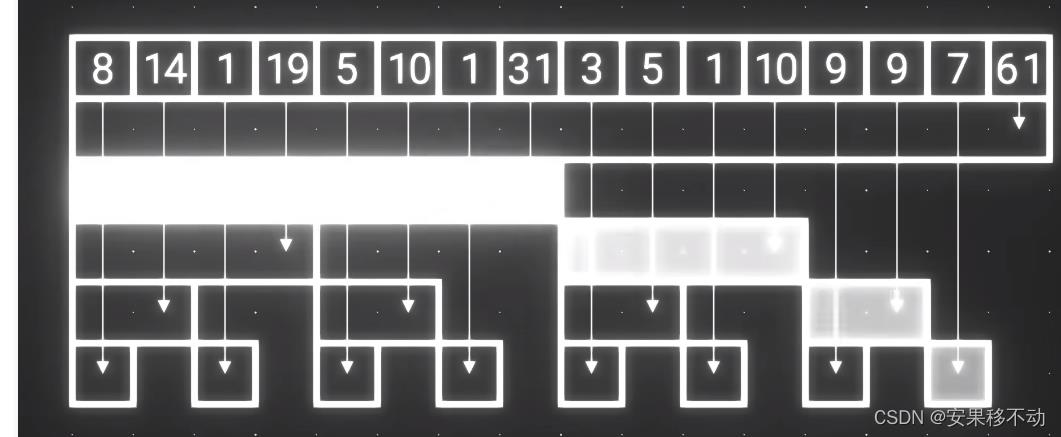
 求和时，我们只需要找到对应区间。将这些区间相加就可以找到答案

修改某个数据时，我们只需要向上找到包含的区间进行修改即可

 

 lowbit的使用 

lowbit 函数 精彩计算。_安果移不动的博客-CSDN博客

package com.example.learn1

fun main() 
    repeat(10) 
        println("当前是：$it 二进制是$it.toUInt().toString(radix = 2) 结果是 $lowBit2(it)")
    

fun lowBit(x: Int): Int 
    return x and (x xor (x - 1))


fun lowBit2(x: Int): Int 
    return x and (-x)

 

 

下面结合lowBit 就要进行计算了。

 

长度为1的数据。lowbit刚好为1

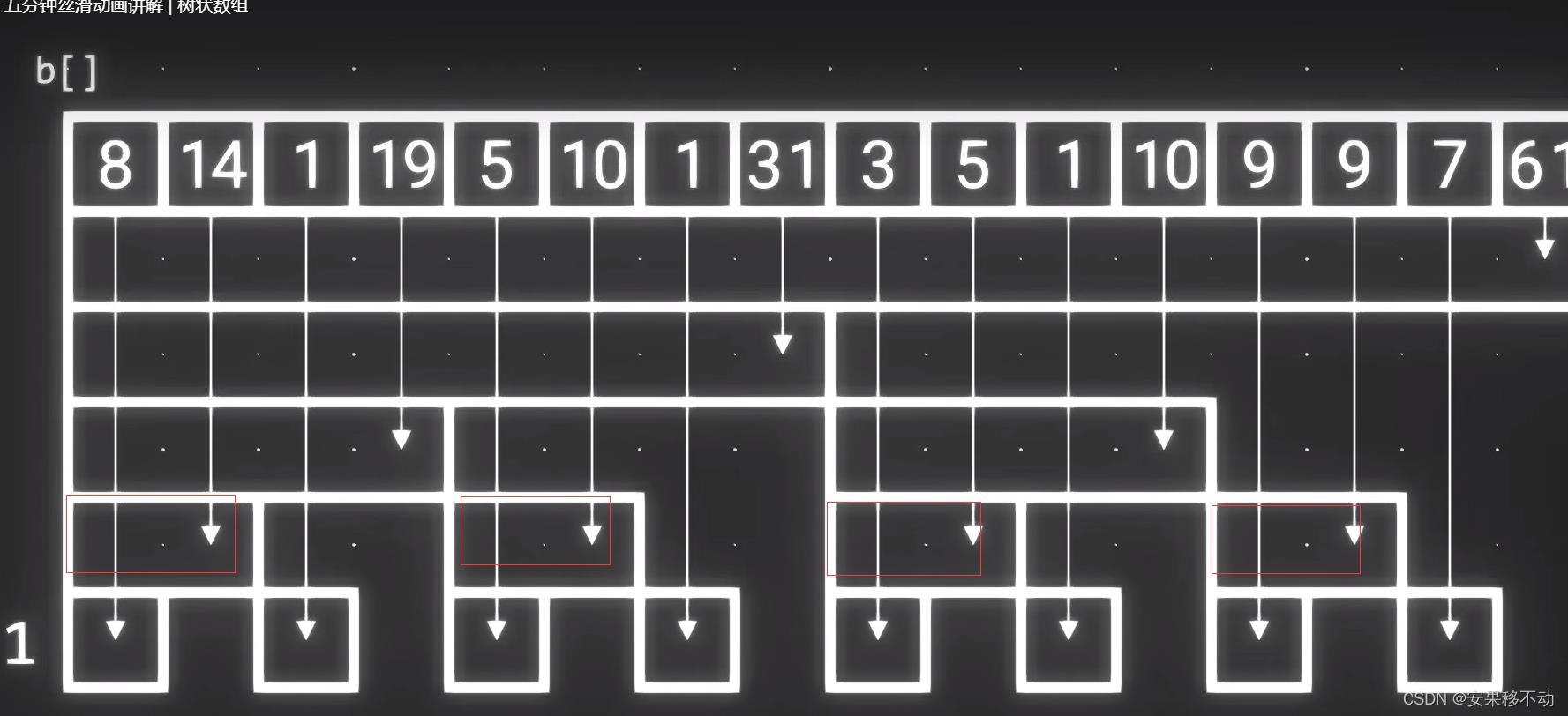
 第二行数据 长度为2 lowBit结果是2.

lowBit 12 结果为多少。是4 他的序号是对少 是12

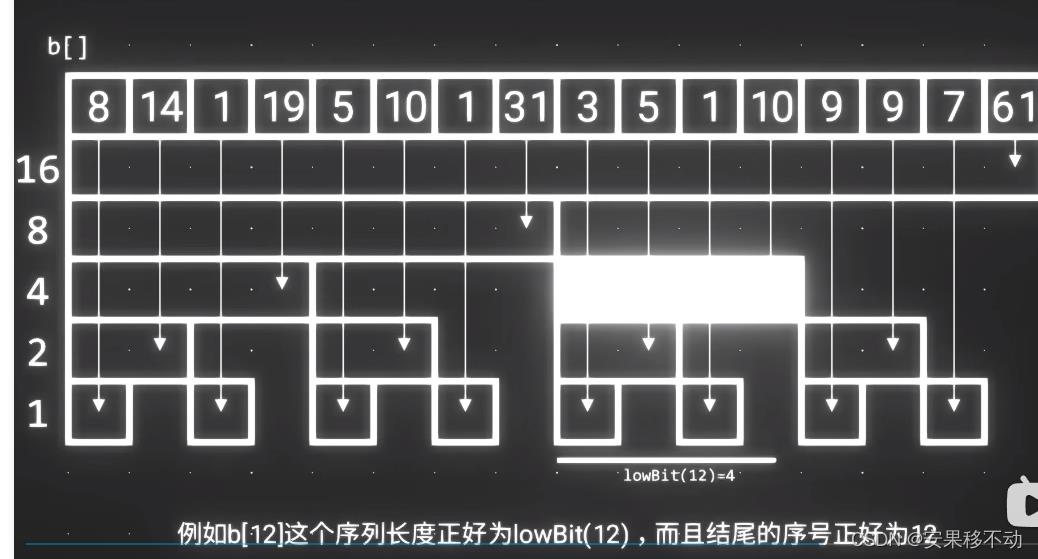
 多带入几个可以发现。

lowBit(i)= 以i为结尾的序列

结论是 序号为i的序列 正好就是长度为lowBit(i) 且以i结尾的序列

有了这个规律后 计算前几个元素的和就简单多了

比如我们要计算前14个元素的和

lowBit(14) = 2

14-lowBit(14)=12

我们只需要计算前12个元素的和然后+b[14] 就对了。

我们来写一个公式

fun count(p: Int, b: List<Int>): Int 
    if (p == 0) 
        return 0
    
    println("p $p ")
    return count(p - lowBit(p), b) + b[p]

 val list = listOf(8, 6, 1, 4, 5, 5, 1, 1, 3, 2, 1, 4, 9, 0, 7, 4)
    println(count(14, list))

 

 14 12 8 然后结果是19

还有一个结论 就是 序列 b[i] 正上方的序列，正好就是 b[i+lowBit(i)]

 

所以修改值的时候只要找到上方的所有序列进行修改。

最终版来咯

fun main() 
    val list = mutableListOf(8, 6, 1, 4, 5, 5, 1, 1, 3, 2, 1, 4, 9, 0, 7, 4)
    println(count(14, list))
    println(finalCount(14, list))
    
    val res = list.subList(0, 14).sum()
    println(res)


fun lowBit(x: Int): Int 
    return x and (x xor (x - 1))


fun lowBit2(x: Int): Int 
    return x and (-x)


fun count(p: Int, b: MutableList<Int>): Int 
    if (p == 0) 
        return 0
    
    return count(p - lowBit(p), b) + b[p]


//修改某个位置的函数
fun changeIndex(p: Int, x: Int, b: MutableList<Int>, N: Int) 
    var tempP = p;
    while (tempP < N) 
        b[tempP] += x;
        tempP += lowBit(p);
    


//上方count 可以改进下。
fun finalCount(p: Int, b: MutableList<Int>): Int 
    var tempP = p;
    var result = 0;
    while (tempP > 0) 
        result += b[tempP];
        tempP -= lowBit(tempP)

    
    return result