使用LLVM分析函数CFG

Posted 2022-09-21 wuhui_gdnt

作者：Eli Bendersky

http://eli.thegreenplace.net/2013/09/16/analyzing-function-cfgs-with-llvm

在Stack Overflow上，关于LLVM一个常见问题是如何构建一个函数的控制流图（CFG），并对它进行拓扑排序，或者拓扑排序的某些变形。为了节省我将来的回答时间，我认为我应该抛出一篇简明的博文，展示LLVM在这个领域的能力。

首先，问这个问题的人通常忘了这个事实：在一个CFG里，基本块（BB）已经组织好了，无需构建一个新的图来运行感兴趣的分析。

每个BB有一组后继者——控制流从这个BB传递到这些BB。很容易通过查看BB的终结符指令获得它（由定义，一个BB有单个终结符）：

// BB is a BasicBlock*

// ...

const TerminatorInst *TInst= BB->getTerminator();

for (unsigned I = 0, NSucc =TInst->getNumSuccessors(); I < NSucc; ++I)

  BasicBlock *Succ =TInst->getSuccessor(I);

  // Do stuff with Succ

BB的这个互联构成了一张图，我们可以任何我们觉得合适的方式遍历之。例如，下面是拓扑排序的一个实现：

classTopoSorter

public:

  void runToposort(const Function &F)

    outs() << "Topological sort of " << F.getName() << ":\\n";

    // Initialize the color map by marking all the vertices white.

    for(Function::const_iterator I = F.begin(), IE = F.end(); I != IE; ++I)

      ColorMap[I] =TopoSorter::WHITE;

   

 

    // The BB graph has a single entry vertex from which the otherBBs should

    // be discoverable - the function entry block.

    bool success =recursiveDFSToposort(&F.getEntryBlock());

    if (success)

      // Now we have all the BBs inside SortedBBs in reversetopological order.

      for(BBVector::const_reverse_iterator RI = SortedBBs.rbegin(),

                                            RE= SortedBBs.rend();

                                            RI!= RE; ++RI)

        outs() << " " <<(*RI)->getName() << "\\n";

     

    else

      outs() << " Sorting failed\\n";

   

 

private:

  enum Color WHITE, GREY,BLACK;

  // Color marks per vertex (BB).

  typedef DenseMap<const BasicBlock *,Color> BBColorMap;

  // Collects vertices (BBs) in "finish" order. Thefirst finished vertex is

  // first, and so on.

  typedefSmallVector<const BasicBlock *, 32> BBVector;

  BBColorMap ColorMap;

  BBVector SortedBBs;

 

  // Helper function to recursively run topological sort from agiven BB.

  // Returns true if the sort succeeded and false otherwise;topological sort

  // may fail if, for example, the graph is not a DAG (detected acycle).

  bool recursiveDFSToposort(const BasicBlock *BB)

    ColorMap[BB] =TopoSorter::GREY;

    // For demonstration, using the lowest-level APIs here. A BB'ssuccessors

    // are determined by looking at its terminator instruction.

    const TerminatorInst *TInst= BB->getTerminator();

    for (unsigned I = 0, NSucc =TInst->getNumSuccessors(); I < NSucc; ++I)

      BasicBlock *Succ =TInst->getSuccessor(I);

      Color SuccColor =ColorMap[Succ];

      if (SuccColor ==TopoSorter::WHITE)

        if(!recursiveDFSToposort(Succ))

          returnfalse;

      elseif (SuccColor ==TopoSorter::GREY)

        // This detects a cycle because grey vertices are all ancestorsof the

        // currently explored vertex (in other words, they're "onthe stack").

        outs() << " Detected cycle: edge from " << BB->getName() <<

                  " to " <<Succ->getName() << "\\n";

        returnfalse;

     

   

    // This BB is finished (fully explored), so we can add it to thevector.

    ColorMap[BB] =TopoSorter::BLACK;

   SortedBBs.push_back(BB);

    returntrue;

 

;

[本文里还包含其他片段的完整代码在这里]

它使用简单的，在Cormen等著的《Introduction to Algorithms》中给出的递归DFS算法。在递归查找期间，在第一次遭遇时，顶点被标记为“灰”，在处理完成时，标记为“黑”。一个完成的顶点所有的外出边都已经被探查了。拓扑排序是所有顶点按完成时刻排序，从最后到第一（这也称为“反后序”）。在我们特定的情形里，一个BB是一个顶点，到其后继者的连接是边。

对这个CFG：

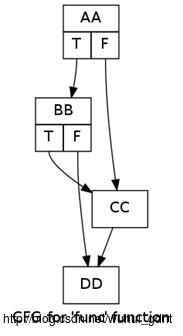
我们得到：

Topological sort of func:

  AA

  BB

  CC

  DD

不过有一个重要的警告。拓扑排序仅对没有环的有向图（DAG）定义了。尽管基本块图是有向的，它不一定是无环的。事实上，代码里的任何循环都翻译为BB图中的一个环。上面的代码检测这并报告一个错误，在找到一个环时拒绝提供排序。例如，考虑这个带有一些环的CFG：

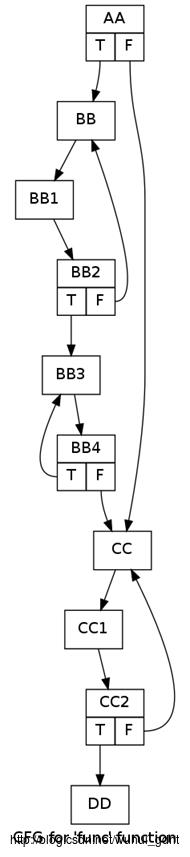
代码将抱怨：

Topological sort of func:

  Detected cycle: edgefrom BB4 to BB3

  Sorting failed

现在我们知道如何辛苦地实现它，让我们看一下LLVM提供的某些有用的工具。头文件llvm/ADT/PostOrderIterator.h提供了以反后序遍历一个函数BB的迭代器。下面是完整的使用片段：

outs() << "Basicblocks of " << F.getName()<< " in post-order:\\n";

for(po_iterator<BasicBlock *> I = po_begin(&F.getEntryBlock()),

                              IE = po_end(&F.getEntryBlock());

                              I != IE; ++I)

  outs() << "  " << (*I)->getName() << "\\n";

回忆拓扑排序是反后序的。因此这正是你需要的顺序，考察来自同一头文件的类ReversePostOrderTraversal。注意也没检测环。在出现环时，这些迭代器将产生某种遍历，但不是拓扑序，因为在这样的情形里它是未定义的。如果你希望一个检测环的工具，在llvm/Analysis/CFG.h里有FindFunctionBackedges。它本质上运行与我上面展示的相同的DFS，虽然使用一个使用栈而不是递归的迭代算法。

关于po_iterator与其亲属的一件趣事是：它们可用于任何类型的图，不只是基本块图。它们可用于过程间分析的函数图，一个表达式图的节点，等等。这个魔法通过GraphTraits机制（llvm/ADT/GraphTraits.h）实现，这将图表示与工作在所有类型图上的实际算法解耦。使之对基本块工作的模板特化可在llvm/Support/CFG.h中找到——在这个头文件里，你还可以找到遍历BB后继（以及前驱）的迭代器，无需手动查询终结者指令。

回到拓扑排序。因为许多有用的函数有循环，因此包含环，我们怎么对付它们？答案是强连同分量（SCC）。如果我们找出BB图的SCC，我们拓扑排序这些SCC，仍然可以进行感兴趣的分析。比如，一个循环通常会收缩为一个SCC。那么我们怎么实现这个？

很幸运，LLVM已经有一个工具可以帮助我们。头文件llvm/ADT/SCCIterator.h定义了scc_iterator在一个图中以后序遍历SCC。这让我们以类似在无环图中排序BB那样的方式，拓扑排序SCC。事实上。在一个无环图中每个BB自己就是一个SCC，因此SCC的做法是一个泛化。使用scc_iterator是容易的：

// Use LLVM's Strongly Connected Components (SCCs) iterator toproduce

// a reverse topological sort of SCCs.

outs() << "SCCsfor " << F.getName() << " in post-order:\\n";

for(scc_iterator<Function *> I = scc_begin(&F),

                             IE = scc_end(&F);

                             I != IE; ++I)

  // Obtain the vector of BBs in this SCC and print it out.

  conststd::vector<BasicBlock *> &SCCBBs = *I;

  outs() << "  SCC: ";

  for(std::vector<BasicBlock *>::const_iterator BBI = SCCBBs.begin(),

                                                 BBIE =SCCBBs.end();

                                                BBI != BBIE; ++BBI)

    outs() <<(*BBI)->getName() << "  ";

 

  outs() << "\\n";

对上面展示的循环CFG，这个代码将打印：

SCCs for func in post-order:

  SCC: DD

  SCC: CC2  CC1  CC

  SCC: BB4  BB3

  SCC: BB2  BB1  BB

  SCC: AA

【注意这是后序，不是反后序；因此显示在列表中的拓扑排序是自底向上的。】

我希望这是一次对LLVM的CFG分析能力有益的审视。代码中我已经给出了许多指示，它们可以作为严肃阅读代码的开端。看一下LLVM为此所拥有的许多工具是相当酷的，看到它们中许多适用各种类型的图特别棒，幸亏GraphTraits机制。