[LeetCode]剑指 Offer 57 - II. 和为s的连续正数序列

Posted 2022-09-03 Spring-_-Bear

输入一个正整数 target ，输出所有和为 target 的连续正整数序列（至少含有两个数）。

序列内的数字由小到大排列，不同序列按照首个数字从小到大排列。

示例 1：

输入：target = 9
输出：[[2,3,4],[4,5]]

示例 2：

输入：target = 15
输出：[[1,2,3,4,5],[4,5,6],[7,8]]

限制：

• 1 <= target <= 10^5

题解一：

求和公式即梯形面积公式：（上底 + 下底）* 高 / 2

设左边界值为 i，右边界值为 j，则 target = (i + j) * (j - i + 1) / 2，即 j*j + j - 2target-i*i+i = 0，在已知 target 和 左边界值 i 的情况下即可通过解一元二次方程求出右边界 j 的值，

根据一元二次方程求根公式得：

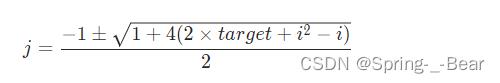
由于 j > i 恒成立，因此直接舍去必为负数的解，即 j 的唯一解求取公式为：

	/**
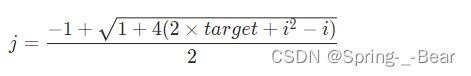
     * 剑指 Offer 57 - II. 和为s的连续正数序列
     */
    public int[][] findContinuousSequence(int target) 
        /*
         * 求和公式（梯形面积公式：（上底 + 下底）* 高 / 2））
         * 设左边界值为 i，右边界值为 j，则 target = (i + j) * (j - i + 1) / 2，
         * 即 j*j + j - 2target-i*i+i = 0，在已知 target 和 左边界值 i 的情况下即可通过解一元二次方程求出右边界 j 的值，
         * 判断 j 为正整数且值大于 i 则有效，有效时将数组序列加入到结果中
         */
        List<int[]> res = new ArrayList<>();
        // 至少含有两个数
        int half = target / 2;
        for (int i = 1; i <= half; i++) 
            double j = (-1 + Math.sqrt(1 + 8L * target + (long) 4 * i * i - 4L * i)) / 2;
            if (j > i && j == (int) j) 
                int[] tmp = new int[(int) j - i + 1];
                for (int k = i; k <= (int) j; k++) 
                    tmp[k - i] = k;
                
                res.add(tmp);
            
        
        return res.toArray(new int[0][]);
    

题解二：

	/**
     * 剑指 Offer 57 - II. 和为s的连续正数序列
     */
    public int[][] findContinuousSequence(int target) 
        /*
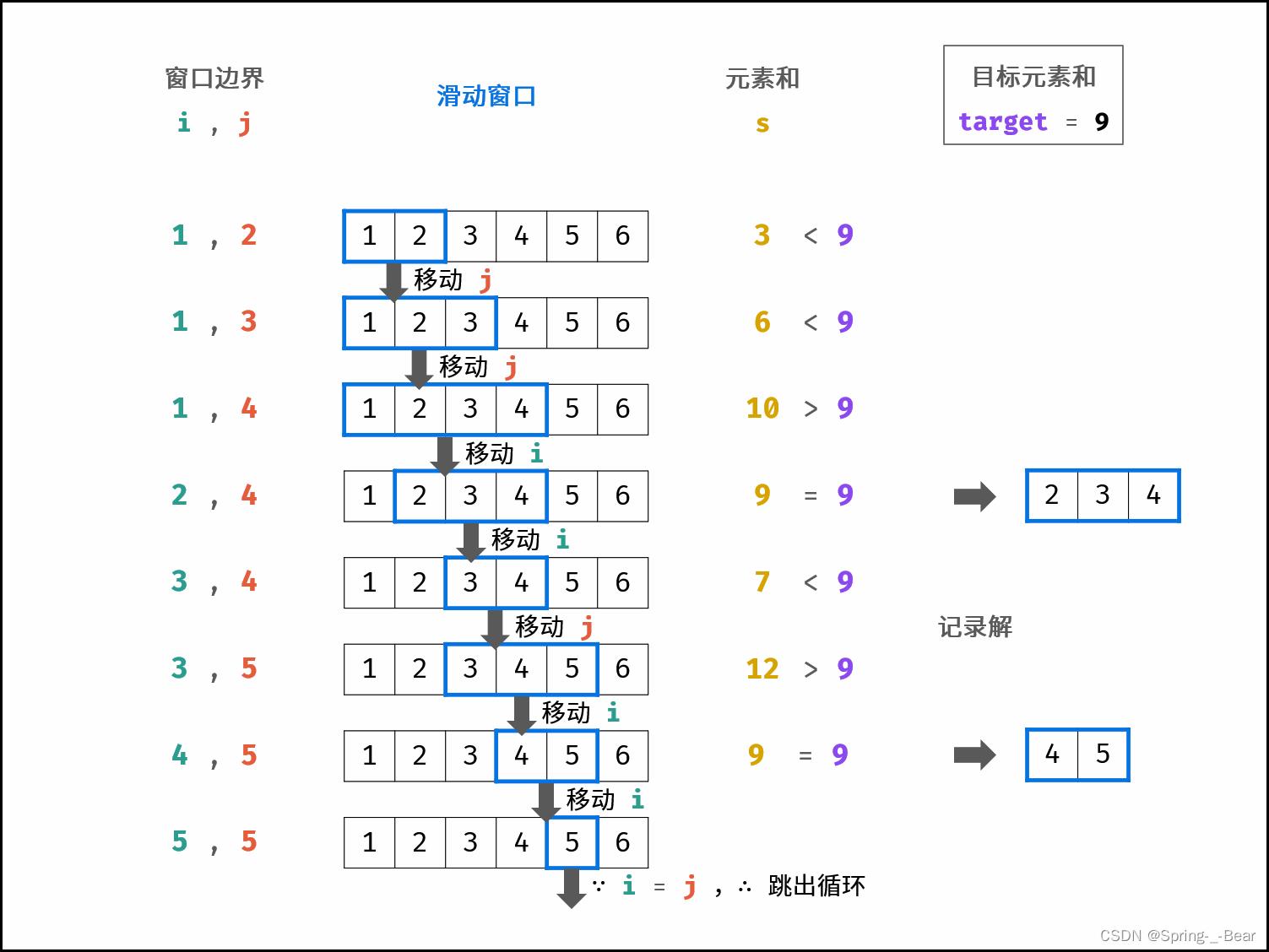
         * 滑动窗口：设连续正整数序列的左边界 i 和右边界 j ，则可构建滑动窗口从左向右滑动。
         * 循环中，每轮判断滑动窗口内元素和与 target 的大小关系，若相等则记录结果，
         * 若大于则移动左边界 i （以减小窗口内的元素和），若小于则移动右边界 j （以增大窗口内的元素和）
         */
        int i = 1;
        int j = 2;
        int sum = 3;
        List<int[]> res = new ArrayList<>();

        while (i < j) 
            if (target == sum) 
                int[] ans = new int[j - i + 1];
                for (int k = i; k <= j; k++) 
                    ans[k - i] = k;
                
                res.add(ans);
            
            if (sum >= target) 
                // 窗口左边界移动，减小元素个数以减小和 sum
                sum -= i;
                i++;
             else 
                // 窗口右边界移动，增加元素个数以增大和 sum
                j++;
                sum += j;
            
        
        return res.toArray(new int[0][]);
    

来源：力扣（LeetCode）
链接：https://leetcode.cn/problems/he-wei-sde-lian-xu-zheng-shu-xu-lie-lcof