《Real-Time Rendering》第四版学习笔记——Chapter 5 Shading Basics

Posted 2023-02-21 董小虫

上半部分：《Real-Time Rendering》第四版学习笔记——Chapter 5 Shading Basics（一）

四、走样和反走样

最原始的显示方式是，当一个三角形覆盖了一个像素的中心，那么该像素就进行着色；否则就不进行着色。这种情况下，图形边缘会产生锯齿。这种情况就叫做走样（aliasing）；而解决这个情况的方法就叫做反走样（antialiasing）。

4.1 采样和滤波理论

渲染图像的处理，其本质就是一个采样（sampling）工作。

采样的目的是为了数字化的表示信息，可以减少信息量。相应的，采样后的信号需要重建（reconstruct）回原来信号。这通过对采样后的信号进行滤波（filtering）来实现。

只要有采样，那么就肯定会出现走样。常见例子：摄像机拍摄告诉旋转的车轮，可能会产生停转或向后旋转的效果；这称为时间映频混扰（temporal aliasing）。在计算机图形学中的例子：边缘的锯齿、闪烁的高光、缩小的纹理等。

走样出现的原因：过低的采样频率。如下图所示，其中蓝线为原信号，绿虚线为重建信号：

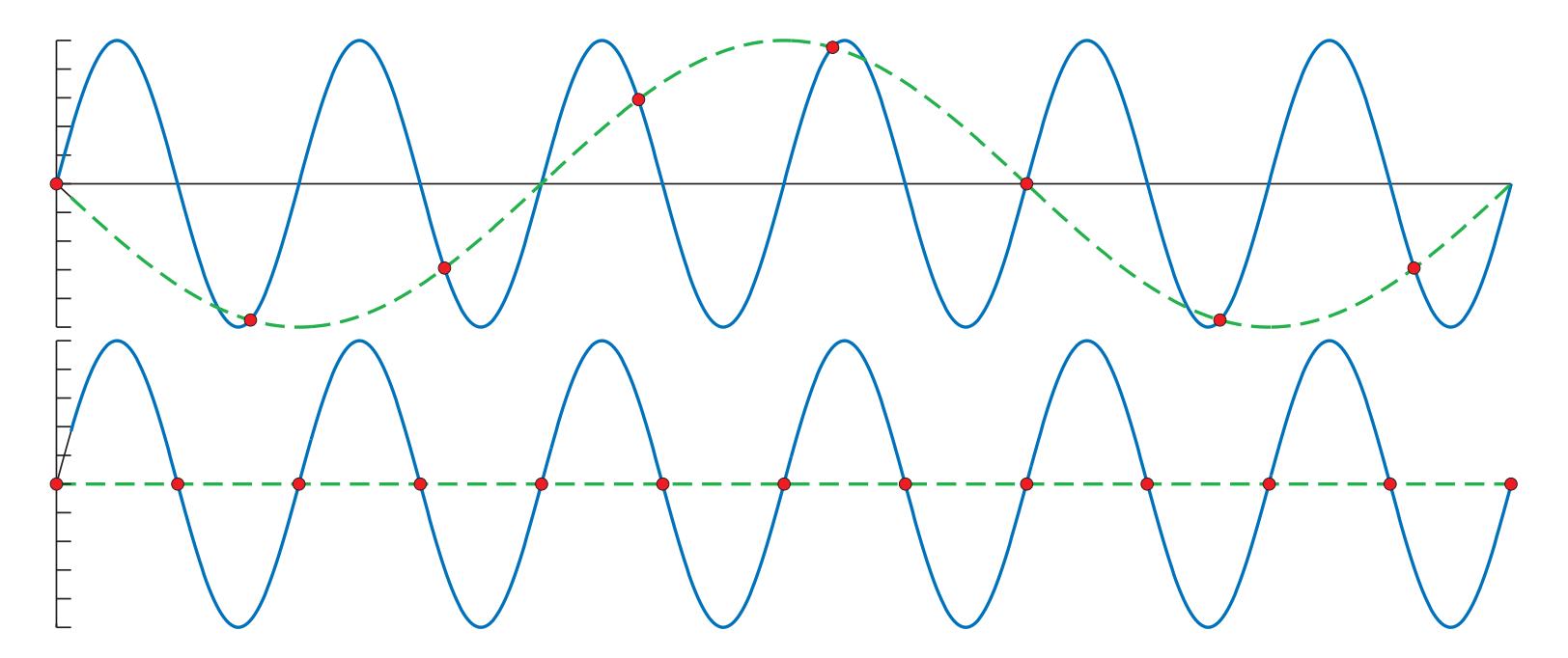
采样定理：只有采样频率大于被采样信号最大频率的两倍以上，才可以得到正确的采样结果。这个采样频率称为Nyquist rate / Nyquist limit。这个频率指明了，信号必须是带宽有限的（band-limited），也就是说在相邻采样点之间要足够的光滑。

通过点采样三维场景，通常不可能是带宽限制的；因为边缘的存在会产生不连续信号，即无穷大频率的信号。所以不可能完全解决走样问题。

信号重建

信号重建需要滤波器。下图为三种常用滤波器，分别为盒滤波器、三角滤波器、辛格滤波器：

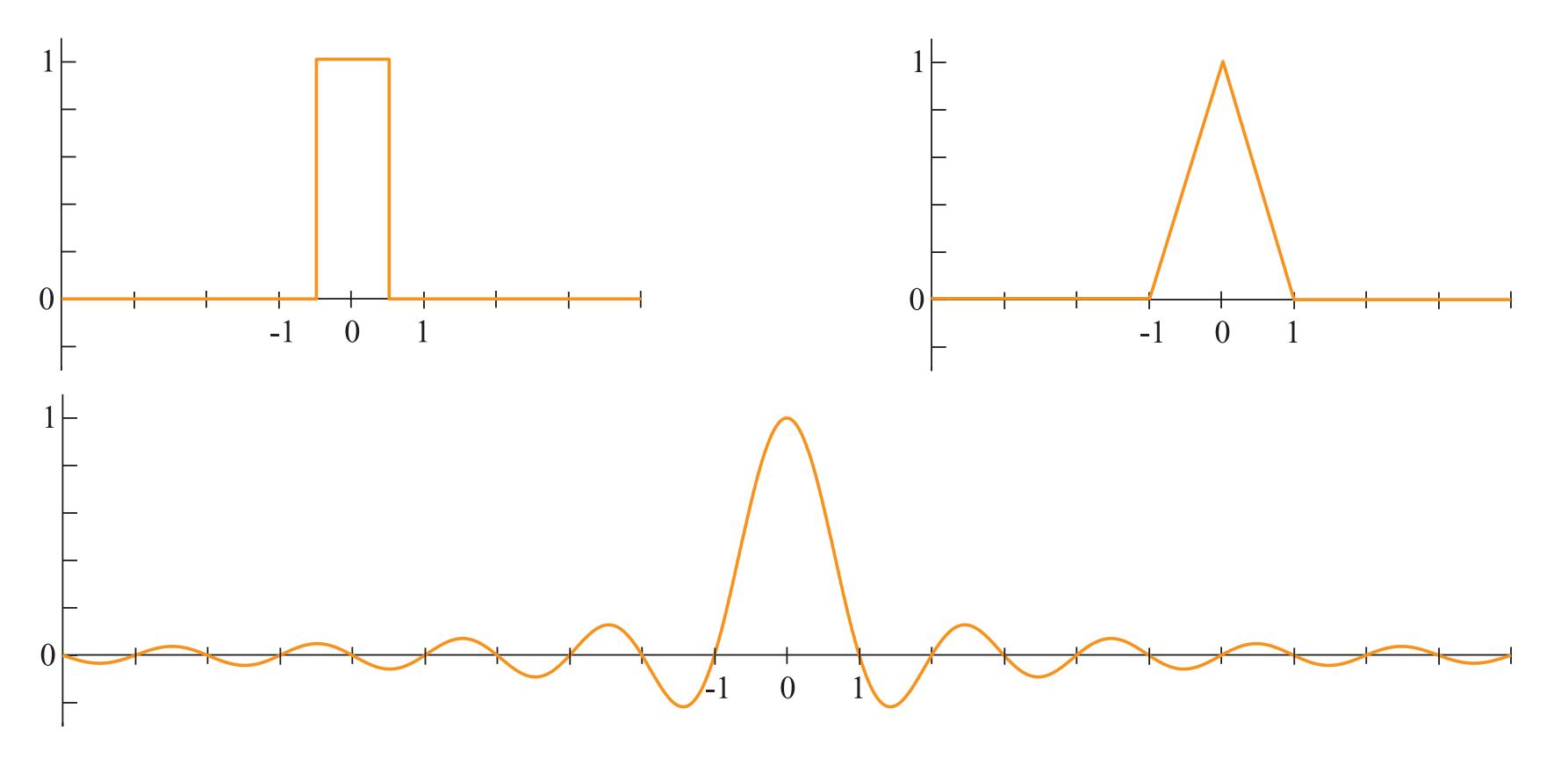
滤波器的函数面积必须为1；否则重建信号会增长或缩水。

信号重建步骤：首先将滤波器置于采样点；然后将滤波器的最高点缩放至采样点大小；最后将所有采样点的结果相加，得到重建信号。

为了得到连续且光滑的重建信号，必须使用低通滤波器（low-pass filter）。傅立叶分析理论解释了，辛格滤波器是一个完美的低通滤波器。辛格滤波器定义为：$\mathrm{s}\mathrm{i}\mathrm{n}\mathrm{c}(x)=\frac{\sin (\pi x)}{\pi x}$。这里乘法操作变为卷积（convolution）函数。

假设采样频率为$f_s$，那么相邻采样点之间的距离为$1/f_s$；那么最佳的信号重建滤波器是$\mathrm{s}\mathrm{i}\mathrm{n}\mathrm{c}(f_{s}x)$，这会消除所有高于$f_s/2$的频率。但辛格函数的宽度是无穷大，切在部分地方是负数，所以并不实用。

在实际应用中，需要一些介于盒滤波器、三角滤波器，和辛格滤波器这两种极端之间的滤波器。

经过滤波，得到的是连续的重建信号。但是计算机图形不能直接显示连续的信号；所以还需要重采样（resample）。

重采样

重采样的作用是放大或缩小一个已采样的信号。假设原采样点之间的距离为单位距离，重采样的点为$a$距离，那么如果$a<1$为放大，又称上采样（upsampling）；$a>1$为缩小，又称下采样（downsampling）。

对于放大而言，假设采样信号已经完美重建，且是连续的。那么直观来看，在需要的区间直接对重建信号进行重采样就行。如下图：

对于缩小而言，原信号的频率过高，导致了采样频率不足以避免走样。这里需要使用$\mathrm{s}\mathrm{i}\mathrm{n}\mathrm{c}(x/a)$的滤波器来进行信号重建，之后就可以根据需要的间隔进行重采样了。这类似于在数字图像中，先进行模糊，再以一个更低的分辨率进行重采样。解决方式如下图所示：

4.2 基于屏幕的反走样

会导致走样的情况：颜色突然变化的地方，如三角形边缘、阴影边缘、镜面高光等。

所有的反走样算法都是基于屏幕的，也就是说，只会在管线的输出采样是执行。且没有一个最好的反走样技术，各有千秋。

基于屏幕的反走样机制的普遍策略是，使用一个采样模式，加权相加所有的采样结果，来生成一个像素颜色：
$$\mathbf{p}(x,y)=\sum _{i=1}^n{w}_i\mathbf{c}(i,x,y)$$
其中$n$是一个像素内的采样次数，函数$\mathbf{c}(i,x,y)$是采样颜色，$w_i$是在$[0,1]$范围内取值的权重。在屏幕网格上的采样位置会根据每个采样而不同，甚至会根据每个像素而采用不同的采样模式。在实时渲染中，通常采用点采样，所以 $\mathbf{c}$可以分成两个函数：通过函数$\mathbf{f}(i,n)$，根据浮点数$(x_f,y_f)$来找到采样位置；通过位置获取精确的颜色。

权重$w_i$总和为1。对于实时渲染，大部分使用均等权重，即$w_i=1/n$。

每个像素采样点数量大于1的反走样算法，称为超采样（supersampling）或过采样（oversampling）。全场景反走样（full-scene antialiasing，FSAA），也叫做超采样反走样（supersampling antialiasing，SSAA）通过在更高的分辨率下渲染场景，然后滤波相邻采样来生成图像。FSAA缺点是影响性能，优点是简单。

基于累加缓存（accumulation buffer）的超采样方法。使用和目的图像相同分辨率的缓存，但是每个颜色通道的位数更多。每次选用像素内的一个采样位置来渲染，$n$次渲染后得到最终结果。缺点：性能消耗过大，一般用于生成极高质量但不关心性能的情况。

多采样反走样（multisampling antialiasing，MSAA）通过逐个像素计算表面着色，以及共享采样结果，来减少计算消耗。对于每个像素，仅执行一次像素着色器：如果所有的采样点都被片段覆盖，那么直接以像素中心来采样；如果部分采样点被覆盖，那么采样位置会调整为更好的表示方式。这种位置调整称为形心采样（centroid sampling）或形心插值（centroid interpolation），这个调整是GPU自动执行的。

NVIDIA的覆盖采样反走样（coverage sampling antialiasing，CSSA）和AMD的增强质量反走样（enhanced quality antialiasing，EQAA），只存储在更高采样率下的片段覆盖率，将采样与覆盖率解耦，减少内存消耗，提升渲染速度。

当所有的几何体都渲染为多采样缓存后，执行分辨（resolve）操作，即计算所有的采样颜色的平均值来确定像素颜色。

使用更宽的滤波器可以减少走样，也会丢失锐利细节。

时域反走样（temporal antialiasing，TAA）是一类使用前帧信息来提升图像质量的技术。其背后的观点是：每帧通过一个很微小的平移，在像素内得到不同的采样位置。当产生的图像数量越多，其均值得到的结果就越好。

TAA的问题：对于静态场景，如果各帧的权重不同，那么会产生热蒸腾闪烁的错误；对于快速移动的场景，则会产生鬼影效果。鬼影的解决方法：

采样模式

有效的采样模式是减少走样的关键。

旋转网格超采样（rotated grid supersampling，RGSS）使用一个旋转的方形模式来解决近似竖直或水平的情况。RGSS模式一种拉丁超立方或N车采样。尽量将采样点分离开，能够提升采样效果。期望使用连续均匀分布的采样点，这可以通过分层采样（stratified sampling）技术来实现。

对于小物体，恒定采样间隔会导致摩尔纹和其他扰动图案。一种解决方法是使用随机采样（stochastic sampling）。

梅花形（quincunx）采样，使采样信息在不同像素之间共享。

FLIPQUAD模式组合了梅花形和RGSS，可以更好的处理接近竖直和水平的情况。其优势是每个像素只需要两个采样；质量接近RGSS。

形态学（Morphological）方法

走样有结构上的特点。基于此，有形态学反走样（morphological antialiasing，MLAA）。着重于寻找并重建边缘。

这是一种后处理方法，即先进行正常的渲染流程，然后再进行反走样。如：亚像素重建反走样（subpixel reconstruction antialiasing，SRAA）、几何缓冲反走样（geometry buffer antialiasing，GBAA）、边缘距离反走样（distance-to-edge antialiasing，DEAA）等。

通用方案是只使用颜色缓冲，这可以使用阴影、高光或其他后处理技术来提升边缘效果。

可以使用更复杂的边缘检测方法，来寻找包含任意角度边缘的像素，并确定其覆盖率。

基于图像的算法存在一些问题：

• 如果颜色相近，那么边缘容易漏检；
• 三个或更多的表面相交于一个像素，很难检测；
• 有高频变化元素的表面，容易误检；
• 物体的角很难检测；
• 曲线很难检测；
• 单像素变化会引起重建的边缘很大的变动；

形态学方法只能使用提供的信息。运行时间受到视野内的内容影响。

总而言之，基于图像的方法可以让反走样占用更少的内存及处理消耗。

五、透明度、Alpha和合成

有很多不同的方法来处理光线穿过半透明物体。这些方法分为两类：

• 基于光的效果：物体引起光衰减和转向，引起其他物体被照亮；
• 基于视角的效果：半透明物体本身如何渲染；

一种给人透明感的方法：网格门半透明（screen-door transparency）。这种方法通过棋盘格填充样式来渲染半透明三角形。每隔一个像素进行渲染，这样可以使后面的物体部分可见。主要的缺点是：只有一个透明物体能够可信地渲染到屏幕。优点是简单。

大部分透明算法通过将透明物体的颜色与其背后物体的颜色进行混合来实现。Alpha混合：alpha（$\alpha$）值描述了不透明度和片段对像素的覆盖率。$\alpha =1.0$表示物体完全不透明，且完全覆盖了像素；$\alpha =0.0$表示像素完全没有遮挡，即片段完全透明。

5.1 混合顺序

通过使用小于$1.0$的alpha值来使物体透明。通过下面的公式，来混合片段的颜色值和像素的原颜色，称为覆盖操作（over operator）：${\mathbf{c}}_o={\alpha }_s{\mathbf{c}}_s+(1-{\alpha }_s){\mathbf{c}}_d$。其中${\mathbf{c}}_s$是透明物体的颜色，成为源（source）；${\alpha }_s$表示物体的alpha值；${\mathbf{c}}_d$表示混合前，像素的颜色，成为目标（destination）；${\mathbf{c}}_o$是结果颜色。通过over操作，可以模拟薄纱类的织物。

正确的渲染顺序：需要在渲染不透明物体之后，再进行透明物体渲染。一般情况下，先关闭混合，绘制不透明物体；再打开混合，绘制透明物体。

深度缓冲每次只能保存一个物体，所以在有多个透明物体存在的情况下受到限制。所以需要知道每个像素的从后到前的渲染顺序。

以从视角方向看的物体形心距离来排序。缺点：该顺序是近似，不准确；物体有交错时，不能正确排序。优点：简单，快速，无需额外内存、无需特殊的GPU支持。

可以修改over操作的公式，使其可以从前往后的顺序混合；这种混合模式称为under操作：
$$\begin{gathered} {\mathbf{c}}_o={\alpha }_d{\mathbf{c}}_d+(1-{\alpha }_d){\alpha }_s{\mathbf{c}}_s, \\ {\mathbf{a}}_o={\alpha }_s(1-{\alpha }_d)+{\alpha }_d={\alpha }_s-{\alpha }_s{\alpha }_d+{\alpha }_d \end{gathered}$$

值得注意的是，alpha值的计算是顺序无关的。

5.2 顺序无关的透明度

under操作可以用于顺序无关透明度（order-independent transparency，OIT）算法，称为深度剥离（depth peeling）。其背后思路是，使用两个深度缓冲和多个pass。具体步骤如下：

1. 第一个pass中，将所有表面的深度值到深度缓冲区；
2. 渲染所有透明物体：如果物体的深度值与深度缓冲区中保存的值相同，表示为最近的透明物体，将其$\text{RGB}\alpha$值保存到独立的颜色缓冲区；如果有超过了第一个深度值，且是最近的，那么保存该透明物体的深度值，以此来“剥离”该层。此时深度值为第二近的透明物体；
3. 后续pass持续剥离，并通过under操作来添加透明层；
4. 最后经过一定数量的pass后，将透明图像融合到不透明图像之上；

OIT优点是可以将最重要的透明层尽早的渲染出来。
OIT的主要问题是：

• 如何获取足够对pass数量；
• 速度慢；每层都需要一个单独的pass；

对该算法的改进，即硬件上的支持方式。。。

5.3 预乘Alpha值和合成

over操作也可以用于照片混合等场景，称为合成（compositing）。这种情况下，每个像素的alpha值会与RGB颜色值一起存储。这种$\text{RGB}\alpha$图像会和其他元素或背景进行混合。

预乘alpha：在使用前，RGB值就已经乘以过了alpha值。这使得over操作更高效：${\mathbf{c}}_o={\mathbf{c}}_{以上是关于《Real-Time\; Rendering》第四版学习笔记——Chapter\; 5\; Shading\; Basics的主要内容，如果未能解决你的问题，请参考以下文章}$

《Real-Time Rendering》第四版学习笔记——Chapter 4 Transforms

《Real-Time Rendering》第四版学习笔记——Chapter 9 Physically Based Shading

《Real-Time Rendering》第四版学习笔记——Chapter 9 Physically Based Shading

《Real-Time Rendering》第四版学习笔记——Chapter 4 Transforms

《Real-Time Rendering》第四版学习笔记——Chapter 4 Transforms

《Real-Time Rendering》第四版学习笔记——Chapter 2 The Graphics Rendering Pipeline