Rescue-Prime hash STARK 代码解析

Posted 2022-08-18 mutourend

1. 引言

前序博客有：

• STARK入门知识
• STARKs and STARK VM: Proofs of Computational Integrity
• STARK中的FRI代码解析
• Rescue-Prime hash STARK

相关代码见：

• https://github.com/aszepieniec/stark-anatomy/blob/master/code（Python）

以Rescue-Prime hash STARK为例。
Rescue-Prime STARK 针对的场景为：

• public info：$h,H$
• private info：$x$
• 待证明relation：$h=H(x)$

其中$H(\ast )$ 为Rescue-Prime hash函数。

Rescue-Prime hash运算中涉及：

• trace：witness信息，Rescue-Prime hash算法中每一轮的输入输出；
• boundary constraints：公开信息，Rescue-Prime hash函数算法中第一轮的补0，以及最后的hash结果；
• transition constraints（又称为AIR constraints）：公开信息，Rescue-Prime hash算法中每一轮的函数运算。

2. Rescue-Prime hash函数

根据Alan Szepieniec等人2020年论文《Rescue-Prime: a Standard Specification (SoK)》可知，Rescue-Prime哈希函数主要参数有$(p,m,c_p,s)$：

• $p$：定义了素数域${\mathbb{F}}_p$，$p$为素数且具有a binary expansion of at least 32 bits。
• $m$：定义了哈希函数的state width。状态由$m>1$个field elements确定。
• $c_p$：为arithmetic sponge的capacity。
  $r_p=m-c_p$
  $r_p$：为该arithmetic sponge的rate，决定了Recue-XLIX permutation之间absorb的field elements数量。
• $80\le s\le 512$：为 target security level，以bits为单位。

此外，还有如下参数：

• $\alpha 和{\alpha }^{-1}$：为S-boxes的幂乘系数。对于所有的$x\in {\mathbb{F}}_p$，有$(x^{\alpha }{)}^{{\alpha }^{-1}}=x$成立。
• $M\in {\mathbb{F}}_p^{m\times m}$：为$m\times m$ MDS矩阵。
• $N\in \mathbb{N}$为round数，一个单一的Rescue-XLIX permutation中包含了$N$个simpler base permutation迭代，这种simpler base permutation称为a round。
• $2mN$个field elements $C_i{}_{i=0}^{2mN-1}$：round constants。

2.1 sponge函数

Rescue-Prime hash函数本质是将任意长的field elements序列 映射为 $r_p$个field elements：
$$f_{R^{\prime }}:{\mathbb{F}}_p^{\ast }\to {\mathbb{F}}_p^{r_p}$$
其在sponge构造中使用了Rescue-XLIX permutation。最终sponge函数会将任意长的序列 映射为 任意长的field elements序列：
$$f_{R^{\prime }-sponge}:{\mathbb{F}}_p^{\ast }\to {\mathbb{F}}^{\star }$$
然后对该sponge函数裁剪，仅获取其前$r_p$个elements作为结果。

在sponge函数的evaluation过程中，包含了：

• 1）a permutation $f_{R^{XLIX}}:{\mathbb{F}}_p^m\to {\mathbb{F}}_p^m$
• 2）具有$m$个field elements的register，称为state。state的初始状态为全零序列 $0\in {\mathbb{F}}_p^m$。
• 3）two phases：absorbing phase以及squeezing phase。

  • 3.1）absorbing阶段：会重复以下流程，直到所有的input elements都吸收完毕：

    • 3.1.1）将input序列中的next $r_p$个elements 与 state的前$r_p$个elements相加；
    • 3.1.2）以与$r_p$个input elements相加后的state为输入，运用permutation $f_{R^{XLIX}}$，获得新的state。

  • 3.2）squeezing阶段：state的前$r_p$个elements即为输出。理论上，可对state递归调用$f_{R^{XLIX}}$获得任意长的output elements序列，不过本文限制为output elements数量最多为$r_p$个。

以input elements长度为$2\ast r_p$为例，相应的absorbing阶段具有2次迭代，示意为：

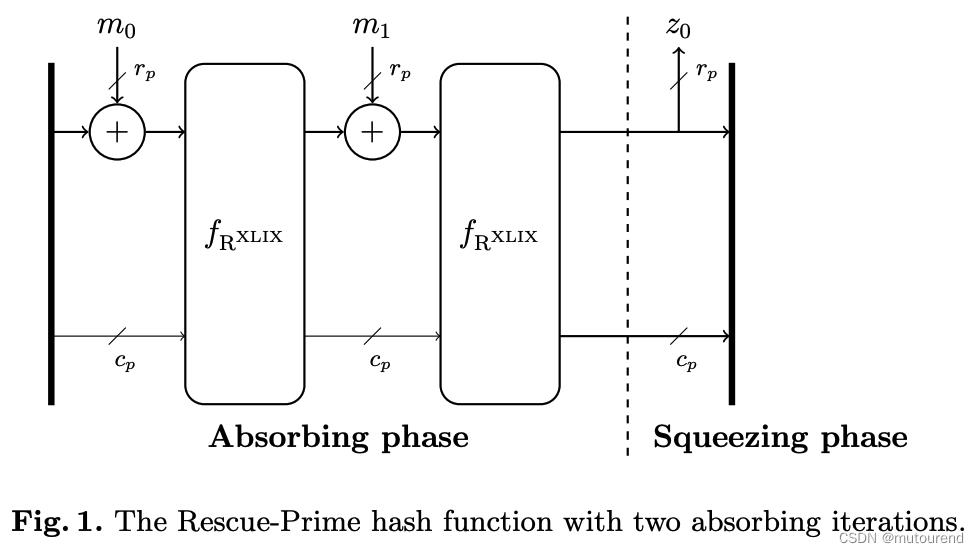
填充Padding：当inputs为任意长度时，sponge函数需要进行填充操作——在inputs之后附加一个$1\in {\mathbb{F}}_p$以及一堆$0\in {\mathbb{F}}_p$，使得填充后的inputs长度为$r_p$的整数倍。
相应的SageMath算法示例为：

2.2 Rescue-XLIX Permutation

Rescue-XLIX Permutation $f_{R^{XLIX}}$中包含了$N$次Rescue-XLIX round函数迭代，单个round中包含了以下6步：

• 1）S-box layer：对state中的每个元素进行power map $(\cdot {)}^{\alpha }$。
• 2）Linear layer：将MDS矩阵 与 state进行 矩阵向量乘法运算。
• 3）Constants injection：从round constants C i i = 0 2 m N − 1 \\C_i\\_i=0^2mN-1 Ci​i=0rescue-prime：基于Goldilocks域的Rescue-Prime 哈希函数加速

  snark/stark-friendly hash函数

  The Goldilocks Prime

  Django——stark组件

  Stark组件

  django 之 stark组件