算法设计与分析--求最大子段和问题(蛮力法分治法动态规划法) C++实现
Posted IT_xiao小巫
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了算法设计与分析--求最大子段和问题(蛮力法分治法动态规划法) C++实现相关的知识,希望对你有一定的参考价值。
算法设计与分析--求最大子段和问题
问题描述:
给定由n个整数组成的序列(a1,a2, …,an),求该序列形如
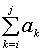
的子段和的最大值,当所有整数均为负整数时,其最大子段和为0。
利用蛮力法求解:
int maxSum(int a[],int n)
int maxSum = 0;
int sum = 0;
for(int i = 0; i < n; i++) //从第一个数开始算起
for(int j = i + 1; j < n; j++)//从i的第二个数开始算起
sum = a[i];
a[i] += a[j];
if(a[i] > sum)
sum = a[i]; //每一趟的最大值
if(sum > maxSum)
maxSum = sum;
return maxSum;
利用分治法求解:
int maxSum(int a[],int left, int right)
int sum = 0;
if(left == right) //如果序列长度为1,直接求解
if(a[left] > 0) sum = a[left];
else sum = 0;
else
int center = (left + right) / 2; //划分
int leftsum = maxSum(a,left,center); //对应情况1,递归求解
int rightsum = maxSum(a, center + 1, right);//对应情况2, 递归求解
int s1 = 0;
int lefts = 0;
for(int i = center; i >= left; i--) //求解s1
lefts += a[i];
if(lefts > s1) s1 = lefts; //左边最大值放在s1
int s2 = 0;
int rights = 0;
for(int j = center + 1; j <= right; j++)//求解s2
rights += a[j];
if(rights > s2) s2 =rights;
sum = s1 + s2; //计算第3钟情况的最大子段和
if(sum < leftsum) sum = leftsum; //合并,在sum、leftsum、rightsum中取最大值
if(sum < rightsum) sum = rightsum;
return sum;
利用动态规划法求解:
int DY_Sum(int a[],int n)
int sum = 0;
int *b = (int *) malloc(n * sizeof(int)); //动态为数组分配空间
b[0] = a[0];
for(int i = 1; i < n; i++)
if(b[i-1] > 0)
b[i] = b[i - 1] + a[i];
else
b[i] = a[i];
for(int j = 0; j < n; j++)
if(b[j] > sum)
sum = b[j];
delete []b; //释放内存
return sum;
完整测试程序:
#include<iostream>
#include<time.h>
#include<Windows.h>
using namespace std;
#define MAX 10000
int BF_Sum(int a[],int n)
int max=0;
int sum=0;
int i,j;
for (i=0;i<n-1;i++)
sum=a[i];
for(j=i+1;j<n;j++)
if(sum>=max)
max=sum;
sum+=a[j];
return max;
int maxSum1(int a[],int left, int right)
int sum = 0;
if(left == right) //如果序列长度为1,直接求解
if(a[left] > 0) sum = a[left];
else sum = 0;
else
int center = (left + right) / 2; //划分
int leftsum = maxSum1(a,left,center); //对应情况1,递归求解
int rightsum = maxSum1(a, center + 1, right);//对应情况2, 递归求解
int s1 = 0;
int lefts = 0;
for(int i = center; i >= left; i--) //求解s1
lefts += a[i];
if(lefts > s1) s1 = lefts; //左边最大值放在s1
int s2 = 0;
int rights = 0;
for(int j = center + 1; j <= right; j++)//求解s2
rights += a[j];
if(rights > s2) s2 =rights;
sum = s1 + s2; //计算第3钟情况的最大子段和
if(sum < leftsum) sum = leftsum; //合并,在sum、leftsum、rightsum中取最大值
if(sum < rightsum) sum = rightsum;
return sum;
int DY_Sum(int a[],int n)
int sum = 0;
int *b = (int *) malloc(n * sizeof(int)); //动态为数组分配空间
b[0] = a[0];
for(int i = 1; i < n; i++)
if(b[i-1] > 0)
b[i] = b[i - 1] + a[i];
else
b[i] = a[i];
for(int j = 0; j < n; j++)
if(b[j] > sum)
sum = b[j];
delete []b; //释放内存
return sum;
int main()
int num[MAX];
int i;
const int n = 40;
LARGE_INTEGER begin,end,frequency;
QueryPerformanceFrequency(&frequency);
//生成随机序列
cout<<"生成随机序列:";
srand(time(0));
for(int i = 0; i < n; i++)
if(rand() % 2 == 0)
num[i] = rand();
else
num[i] = (-1) * rand();
if(n < 100)
cout<<num[i]<<" ";
cout<<endl;
//蛮力法//
cout<<"\\n蛮力法:"<<endl;
cout<"最大字段和:";
QueryPerformanceCounter(&begin);
cout<<BF_Sum(num,n)<<endl;
QueryPerformanceCounter(&end);
cout<<"时间:"
<<(double)(end.QuadPart - begin.QuadPart) / frequency.QuadPart
<<"s"<<endl;
cout<<"\\n分治法:"<<endl;
cout<"最大字段和:";
QueryPerformanceCounter(&begin);
cout<<maxSum1(num,0,n)<<endl;
QueryPerformanceCounter(&end);
cout<<"时间:"
<<(double)(end.QuadPart - begin.QuadPart) / frequency.QuadPart
<<"s"<<endl;
cout<<"\\n动态规划法:"<<endl;
cout<"最大字段和:";
QueryPerformanceCounter(&begin);
cout<<DY_Sum(num,n)<<endl;
QueryPerformanceCounter(&end);
cout<<"时间:"
<<(double)(end.QuadPart - begin.QuadPart) / frequency.QuadPart
<<"s"<<endl;
system("pause");
return 0;
测试结果:
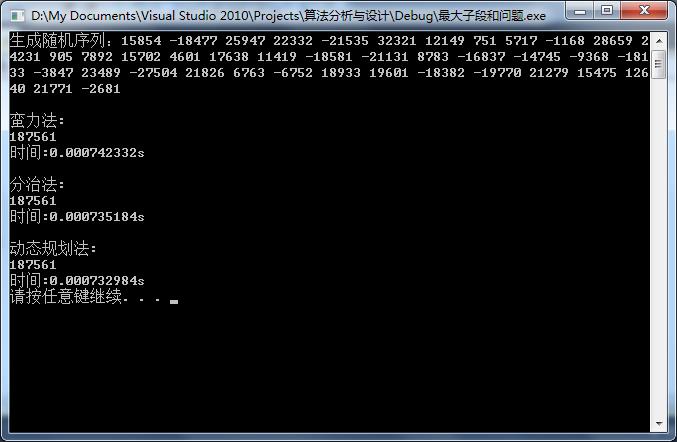
以上是关于算法设计与分析--求最大子段和问题(蛮力法分治法动态规划法) C++实现的主要内容,如果未能解决你的问题,请参考以下文章