基于SNN脉冲神经网络的Hebbian学习训练过程matlab仿真
Posted fpga和matlab
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了基于SNN脉冲神经网络的Hebbian学习训练过程matlab仿真相关的知识,希望对你有一定的参考价值。
目录
一、理论基础
近年来,深度学习彻底改变了机器学习领域,尤其是计算机视觉。在这种方法中,使用反向传播以监督的方式训练深层(多层)人工神经网络(ANN)。虽然需要大量带标签的训练样本,但是最终的分类准确性确实令人印象深刻,有时甚至胜过人类。人工神经网络中的神经元的特征在于单个、静态、连续值的激活。然而生物神经元使用离散的脉冲来计算和传输信息,并且除了脉冲发放率外,脉冲时间也很重要。因此脉冲神经网络(SNN)在生物学上比ANN更现实,并且如果有人想了解大脑的计算方式,它无疑是唯一可行的选择。 SNN也比ANN更具硬件友好性和能源效率,因此对技术,尤其是便携式设备具有吸引力。但是训练深度SNN仍然是一个挑战。脉冲神经元的传递函数通常是不可微的,从而阻止了反向传播。在这里,我们回顾了用于训练深度SNN的最新监督和无监督方法,并在准确性、计算成本和硬件友好性方面进行了比较。目前的情况是,SNN在准确性方面仍落后于ANN,但差距正在缩小,甚至在某些任务上可能消失,而SNN通常只需要更少的操作。
SNN中的无监督学习通常将STDP纳入学习机制。生物STDP的最常见形式具有非常直观的解释。如果突触前神经元在突触后神经元之前不久触发(大约10毫秒),则连接它们的权重会增加。如果突触后神经元在突触后神经元后不久触发,则时间事件之间的因果关系是虚假的,权重会减弱。增强称为长时程增强(LTP),减弱称为长时程抑制(LTD)。短语“长时程”用于区分实验中观察到的几毫秒范围内的非常短暂的影响。
下面的公式是通过拟合实验数据对一对脉冲进行了实验上最常见的STDP规则的理想化。
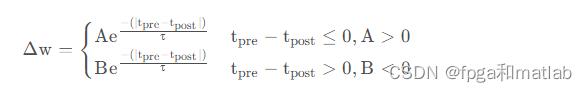
以上公式中的第一种情况描述LTP,而第二种情况描述LTD。效果的强度由衰减指数调制,衰减指数的大小由突触前和突触后脉冲之间的时间常数比例时间差控制。人工SNN很少使用此确切规则。他们通常使用变体,以实现更多的简单性或满足便利的数学特性。
二、案例背景
1.问题描述
SNN神经网络的学习方法也不是很好,作为传统的基于速率的网络而发展,使用反向传播学习算法。使用高效的Hebbian学习方法:棘突神经元网络的稳态。类似于STDP,尖峰之间的计时用于突触修饰。内稳态确保了突触权重是有界的学习是稳定的。赢家通吃机制也很重要实施以促进输出之间的竞争性学习神经元。我们已经在一个C++对象中实现了这个方法面向对象的代码(称为CSpike)。我们已经在四个服务器上测试了代码Gabor滤波器的图像,并发现钟形调谐曲线使用不同类型的Gabor滤波器的36个测试集图像方向。这些钟形曲线与这些曲线相似实验上观察到的V1和MT/V5区域哺乳动物的大脑。
2.思路流程
SNN即目前的最新的第三代神经网络,具体的仿真步骤如下所示:
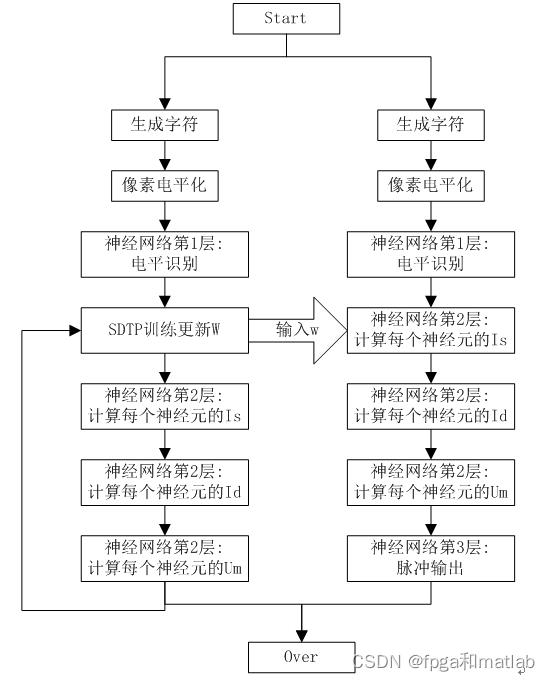
三、部分MATLAB仿真
matlab仿真程序如下所示:
clc;
clear;
close all;
warning off;
addpath 'func\\'
RandStream.setDefaultStream(RandStream('mt19937ar','seed',1));
%%
load Character\\Character_set.mat
%显示论文fig1. character set used
func_view_character;
%**************************************************************************
%%
%显示论文fig2. Representation of 'A'
A_Line = Representation_Character(A_ch);
figure;
stem(1:5*3,A_Line,'LineWidth',2);
hold on
stairs(1:5*3,A_Line,'r');
axis([0,5*3+1,-0.25,1.25]);
title('Fig.2. Representation of A');
%**************************************************************************
%% 以下是程序的第一部分,即4个字符的仿真
%建立SNN神经网络模型
Rm = 80;
theta = 10; %10mv
rs = 2; %2ms
rm = 30; %30ms
rmin = 2; %2ms
rmax = 30; %30ms;
lin = 0.3;
lin_dec = 0.05;
A1 = 0.1;
A2 =-0.105;
r1 = 1; %1ms
r2 = 1; %1ms
tstep = 0.2; %0.2ms;
times = 200; %训练次数
error = 1e-3;%训练目标误差
vth = 7;
%通过神经网络对A,B,C,D进行训练识别
%对应论文fig.3. Output when each character is presented individually
%随机产生初始的权值wij
N_in = 15;
w_initial = 0.5+0.5*rand(N_in,4);
for i = 1:times
wi = w_initial;
end
w0 = w_initial;
dew = 0;
wmax = 0;
wmin = 0;
det = zeros(N_in,4);
tpre = 300*ones(N_in,times);
tpost = 301*ones(N_in,times);
Time2 = 4000;
dt = 0.05;
STIME = 24;
%%
%字符转换为电平
A_Line = Representation_Character(A_ch);
B_Line = Representation_Character(B_ch);
C_Line = Representation_Character(C_ch);
D_Line = Representation_Character(D_ch);
Lines = [A_Line B_Line C_Line D_Line];
for num = 1:4
Dat = Lines(:,num);
for ij = 1:1
for i = 1:times
wi = w_initial;
end
ind = 0;
for i = 1:times
i
ind = ind + 1;
%计算rd
for n1 = 1:N_in
rd(n1) = rmax - abs(wi(n1))*(rmax - rmin);
end
%计算Rd
for n1 = 1:N_in
Rd(n1) = (rd(n1)*theta/Rm) * (rm/rd(n1))^(rm/(rm-rd(n1)));
end
%计算delta t
for n1 = 1:N_in
if Dat(n1) == 1
det(n1) = tpre(n1,i) - tpost(n1,i);
else
det(n1) = -(tpre(n1,i) - tpost(n1,i));
end
end
%计算delta w
for n1 = 1:N_in
if det(n1) <= 0
dew(n1) = A1*exp( det(n1)/r1);
else
dew(n1) = A2*exp(-det(n1)/r2);
end
if i > 1
%计算权值更新
if dew(n1) > 0
wi(n1) = wi-1(n1) + lin*dew(n1)*(wi-1(n1));
else
wi(n1) = wi-1(n1) + lin*dew(n1)*(wi-1(n1));
end
end
end
%计算Id
for n1 = 1:N_in
Idn1 = func_Id(Rd(n1),rd(n1),wi(n1),Dat(n1),Time2,dt,tpre(n1,i));
end
%计算Is
Is = func_Is(N_in,rs,wi,Dat,Time2,dt,tpre(n1,i));
%计算u
Um = func_um(N_in,wi,Rm,Id,Is,rm,Time2,dt,Dat,tpre(n1,i),vth);
%计算训练误差
if i > 1
err2(ind-1) = abs(norm(wi/max(wi)) - norm(wi-1/max(wi-1)));
if abs(norm(wi/max(wi) - norm(wi-1/max(wi-1)))) <= error
break;
end
end
end
end
Ws(:,num) = wend/max(wend);
clear Is Id Um w
end
%%
%训练完之后进行测试
%A测试
%A测试
UmA = [];
for ij = 1:STIME
ij
for j = 1:4
ind = 0;
ind = ind + 1;
%计算Id
for n1 = 1:N_in
Idn1 = func_Id(Rd(n1),rd(n1),Ws(n1,1),Lines(n1,j),Time2,dt,tpre(n1,j));
end
%计算Is
Isj = func_Is(N_in,rs,Ws(:,1),Lines(:,j),Time2,dt,tpre(n1,j));
%计算u
Um(j,:) = func_um(N_in,Ws(:,1),Rm,Id,Isj,rm,Time2,dt,Lines(:,j),tpre(n1,j),vth);
end
UmA = [UmA,Um];
end
figure;
plot(1:Time2*STIME,UmA(1,:),'r');
hold on
plot(1:Time2*STIME,UmA(2,:),'g');
hold on
plot(1:Time2*STIME,UmA(3,:),'b');
hold on
plot(1:Time2*STIME,UmA(4,:),'c');
hold off
legend('Neuron1','Neuron2','Neuron3','Neuron4');
axis([1,Time2*STIME,0,30]);
clear Id Is Um w
%B测试
%B测试
UmB = [];
for ij = 1:STIME
ij
for j = 1:4
ind = 0;
ind = ind + 1;
%计算Id
for n1 = 1:N_in
Idn1 = func_Id(Rd(n1),rd(n1),Ws(n1,2),Lines(n1,j),Time2,dt,tpre(n1,j));
end
%计算Is
Isj = func_Is(N_in,rs,Ws(:,2),Lines(:,j),Time2,dt,tpre(n1,j));
%计算u
Um(j,:) = func_um(N_in,Ws(:,2),Rm,Id,Isj,rm,Time2,dt,Lines(:,j),tpre(n1,j),vth);
end
UmB = [UmB,Um];
end
figure;
plot(1:Time2*STIME,UmB(1,:),'r');
hold on
plot(1:Time2*STIME,UmB(2,:),'g');
hold on
plot(1:Time2*STIME,UmB(3,:),'b');
hold on
plot(1:Time2*STIME,UmB(4,:),'c');
hold off
legend('Neuron1','Neuron2','Neuron3','Neuron4');
axis([1,Time2*STIME,0,30]);
clear Id Is Um w
%C测试
%C测试
UmC = [];
for ij = 1:STIME
ij
for j = 1:4
ind = 0;
ind = ind + 1;
%计算Id
for n1 = 1:N_in
Idn1 = func_Id(Rd(n1),rd(n1),Ws(n1,3),Lines(n1,j),Time2,dt,tpre(n1,j));
end
%计算Is
Isj = func_Is(N_in,rs,Ws(:,3),Lines(:,j),Time2,dt,tpre(n1,j));
%计算u
Um(j,:) = func_um(N_in,Ws(:,3),Rm,Id,Isj,rm,Time2,dt,Lines(:,j),tpre(n1,j),vth);
end
UmC = [UmC,Um];
end
figure;
plot(1:Time2*STIME,UmC(1,:),'r');
hold on
plot(1:Time2*STIME,UmC(2,:),'g');
hold on
plot(1:Time2*STIME,UmC(3,:),'b');
hold on
plot(1:Time2*STIME,UmC(4,:),'c');
hold off
legend('Neuron1','Neuron2','Neuron3','Neuron4');
axis([1,Time2*STIME,0,30]);
clear Id Is Um w
%D测试
%D测试
UmD = [];
for ij = 1:STIME
ij
for j = 1:4
ind = 0;
ind = ind + 1;
%计算Id
for n1 = 1:N_in
Idn1 = func_Id(Rd(n1),rd(n1),Ws(n1,4),Lines(n1,j),Time2,dt,tpre(n1,j));
end
%计算Is
Isj = func_Is(N_in,rs,Ws(:,4),Lines(:,j),Time2,dt,tpre(n1,j));
%计算u
Um(j,:) = func_um(N_in,Ws(:,4),Rm,Id,Isj,rm,Time2,dt,Lines(:,j),tpre(n1,j),vth);
end
UmD = [UmD,Um];
end
figure;
plot(1:Time2*STIME,UmD(1,:),'r');
hold on
plot(1:Time2*STIME,UmD(2,:),'g');
hold on
plot(1:Time2*STIME,UmD(3,:),'b');
hold on
plot(1:Time2*STIME,UmD(4,:),'c');
hold off
legend('Neuron1','Neuron2','Neuron3','Neuron4');
axis([1,Time2*STIME,0,30]);
clear Id Is Um w
%连续码流测试
%连续码流测试
Umss = [];
for ij = 1:STIME
ij
if ij>=1 &ij <= 2
W = Ws(:,3);
end
if ij>=3 &ij <= 5
W = Ws(:,4);
end
if ij>=6 &ij <= 8
W = Ws(:,1);
end
if ij>=9 &ij <= 12
W = Ws(:,3);
end
if ij>=13 &ij <= 15
W = Ws(:,1);
end
if ij>=16 &ij <= 18
W = Ws(:,2);
end
if ij>=19 &ij <= 21
W = Ws(:,3);
end
if ij>=22 &ij <= 24
W = Ws(:,4);
end
for j = 1:4
ind = 0;
ind = ind + 1;
%计算Id
for n1 = 1:N_in
Idn1 = func_Id(Rd(n1),rd(n1),W(n1),Lines(n1,j),Time2,dt,tpre(n1,j));
end
%计算Is
Isj = func_Is(N_in,rs,W,Lines(:,j),Time2,dt,tpre(n1,j));
%计算u
Um(j,:) = func_um(N_in,W,Rm,Id,Isj,rm,Time2,dt,Lines(:,j),tpre(n1,j),vth);
end
Umss = [Umss,Um];
end
figure;
plot(1:Time2*STIME,Umss(1,:),'r');
hold on
plot(1:Time2*STIME,Umss(2,:),'g');
hold on
plot(1:Time2*STIME,Umss(3,:),'b');
hold on
plot(1:Time2*STIME,Umss(4,:),'c');
hold off
legend('Neuron1','Neuron2','Neuron3','Neuron4');
axis([1,Time2*STIME,0,30]);
clear Id Is Um w
%%
%Fig.5.Weight distribution
figure;
subplot(121);
bar3(w0(1:15,:),0.8,'r');hold on
bar3(w0(1:12,:),0.8,'y');hold on
bar3(w0(1:9,:) ,0.8,'g');hold on
bar3(w0(1:6,:) ,0.8,'c');hold on
bar3(w0(1:3,:) ,0.8,'b');hold on
xlabel('Output Neruon');
ylabel('Input Neruon');
zlabel('Weight');
title('Before training');
axis([0,5,0,16,0,1.3]);
view([-126,36]);
subplot(122);
bar3(Ws(1:15,:),0.8,'r');hold on
bar3(Ws(1:12,:),0.8,'y');hold on
bar3(Ws(1:9,:) ,0.8,'g');hold on
bar3(Ws(1:6,:) ,0.8,'c');hold on
bar3(Ws(1:3,:) ,0.8,'b');hold on
xlabel('Output Neruon');
ylabel('Input Neruon');
zlabel('Weight');
title('After training');
axis([0,5,0,16,0,1.3]);
view([-126,36]);
四、仿真结论分析
将SNN进行仿真,并得到类似论文中的仿真效果,具体的仿真结果如下图所示:
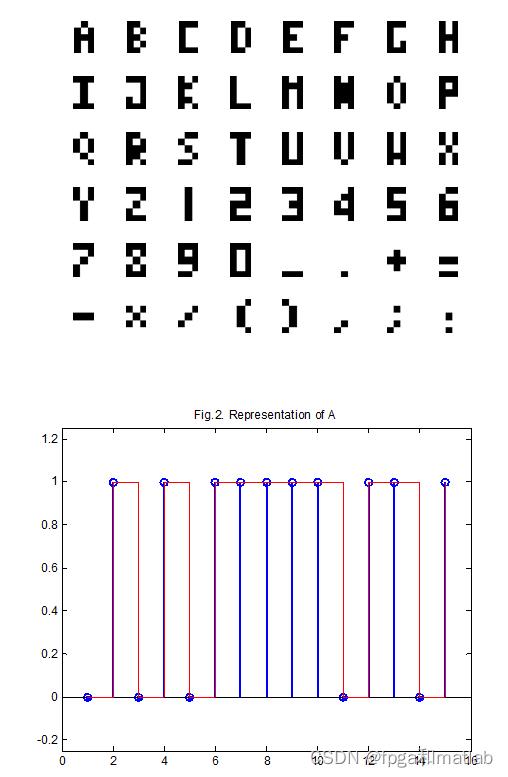
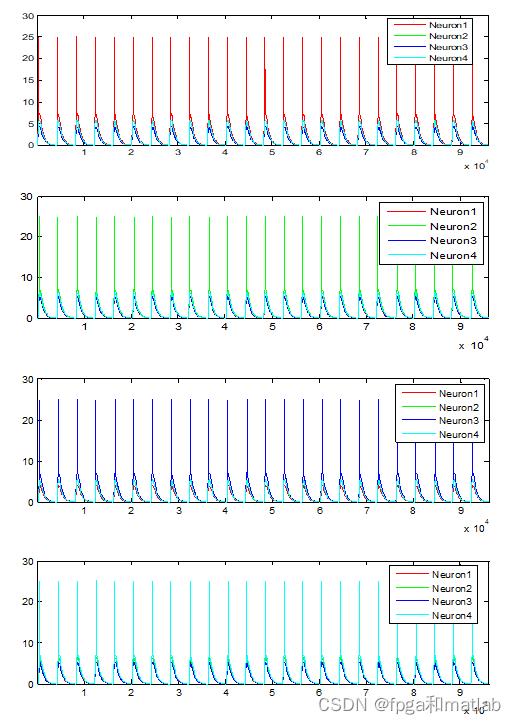
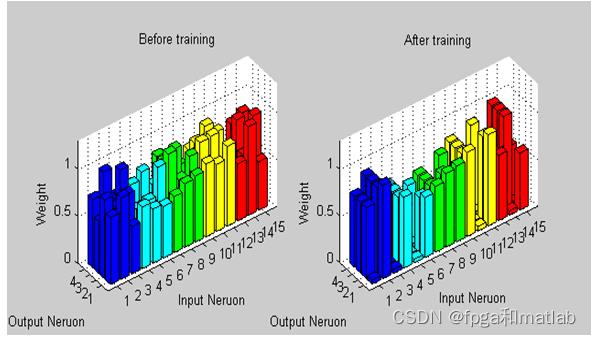
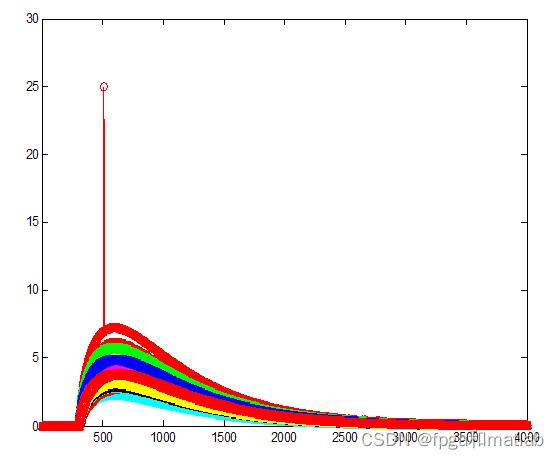
上述就是实际的仿真效果图。
五、参考文献
[1] Gupta A , Long L N . Hebbian learning with winner take all for spiking neural networks[C]// International Joint Conference on Neural Networks. IEEE, 2009.A05-12
以上是关于基于SNN脉冲神经网络的Hebbian学习训练过程matlab仿真的主要内容,如果未能解决你的问题,请参考以下文章