递归：理解和应用

Posted 2022-08-10 我家大宝最可爱

从一个最最简单的例子出发，我们要对一个数组进行求和，一个想当然的方法就是直接进行遍历求和，我们看看能否考虑使用递归。

递归算法是一种直接或者间接调用自身函数或者方法的算法。说简单了就是程序自身的调用。递归算法就是将原问题不断分解为规模缩小的子问题，然后递归调用方法来表示问题的解。（用同一个方法去解决规模不同的问题）

• 递去：将递归问题分解为若干个规模较小，与原问题形式相同的子问题，这些子问题可以用相同的解题思路来解决
• 归来：当你将问题不断缩小规模递去的时候，必须有一个明确的结束递去的临界点（递归出口），一旦达到这个临界点即就从该点原路返回到原点，最终问题得到解决。
  四、递归算法的设计要素

递归思维是一种从下向上的思维方式，使用递归算法往往可以简化我们的代码，而且还帮我们解决了很复杂的问题。递归算法的难点就在于它的逻辑性，一般设计递归算法需要考虑以下几点:

1. 明确递归的终止条件
2. 提取重复的逻辑，缩小问题的规模不断递去
3. 给出递归终止时的处理办法

什么时候使用递归

判断一个问题是否可以使用递归才是掌握递归的开始。先看几个经典的递归问题

1. 顺序打印链表

看到这个问题，最简单的想法就是循环了，老实说考虑使用递归去解的我都觉得是脑子有问题，无奈为了慢慢理解递归只能强行往上靠。
我考虑的时候是非常直接，打印当前的数字，然后递归的调用自身不断缩小问题规模

# Definition for singly-linked list.
# class ListNode:
#     def __init__(self, x):
#         self.val = x
#         self.next = None

class Solution:
    def printList(self, head: ListNode) -> List[int]:
        if head is None:
            return
        print(head.val)
        self.printList(head.next)

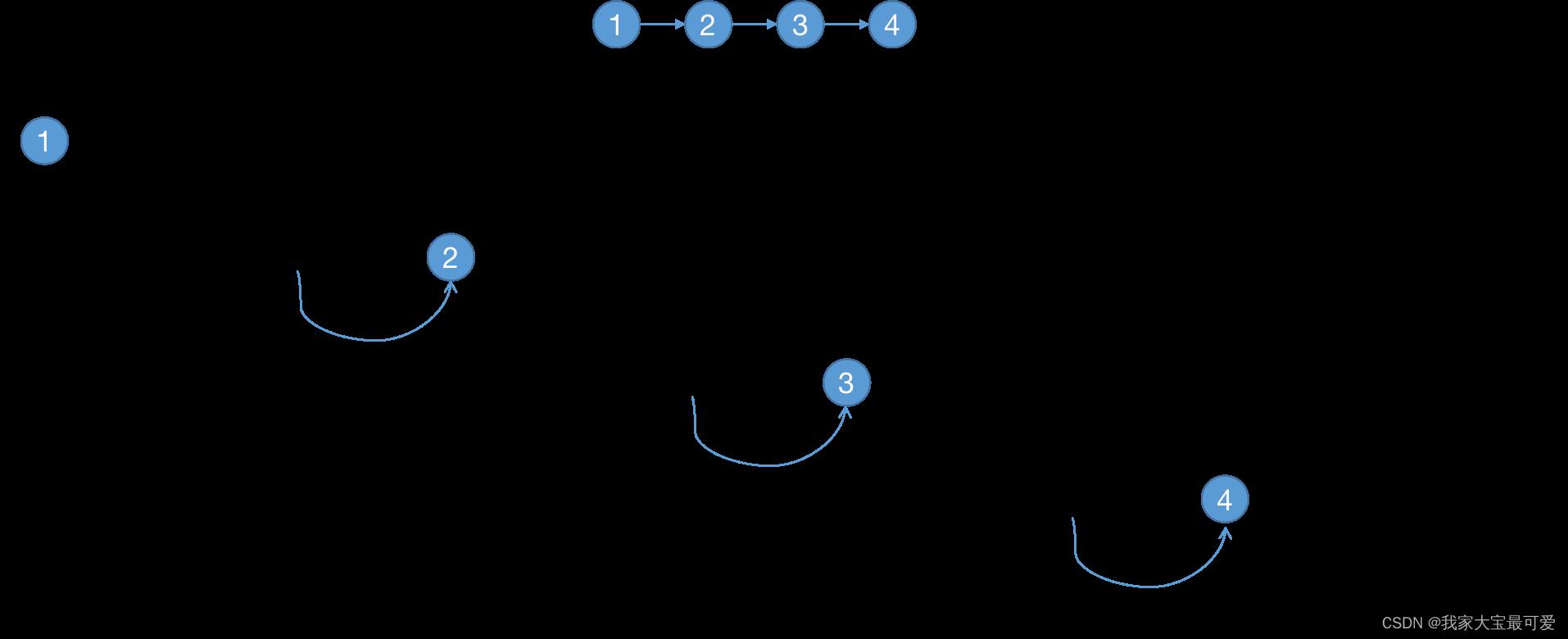
1. 明确了递归的停止条件，head is None的时候到了链表的末尾了，无需进一步打印因此可以停止了
2. 提取重复的逻辑，这里的重复逻辑非常的简单，就是print(head.val)
3. 缩小问题规模，我们不断调用head.next，使得head往链表后面移动，缩小了问题规模
4. 递归终止的时候我们也无需做其他事情，因此直接返回即可

老实讲，这里的递归其实就是for循环，我们不断的往后遍历。

2. 链表求和

链表求和和打印是一样的，我们使用递归遍历每一个元素然后求和即可。但是这里考虑的是递归的子问题。

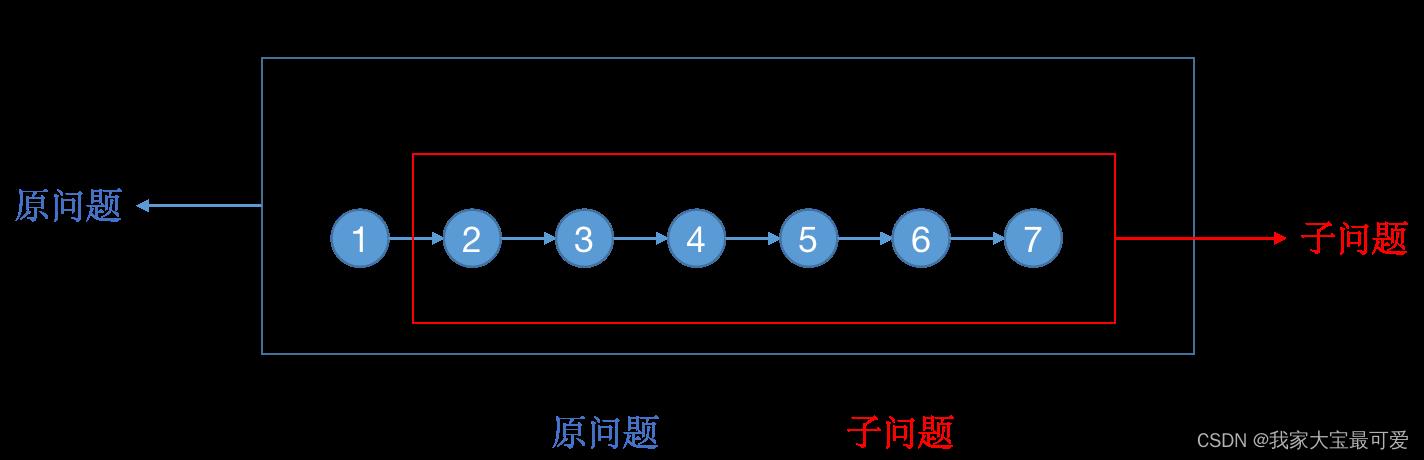
从上图也可以很容易明白，我们可以缩小问题规模的，想要求解sum([1,2,3,4,5,6,7])，我们只要先求出sum([2,3,4,5,6,7])的结果，然后再跟head.val相加即可。同样的套娃方式，我们想要求解sum([2,3,4,5,6,7])，只需要求解sum([3,4,5,6,7])即可。

# Definition for singly-linked list.
# class ListNode:
#     def __init__(self, x):
#         self.val = x
#         self.next = None

class Solution:
    def listSum(self, head: ListNode) -> List[int]:
        if head is None:
            return 0
        s = self.listSum(head.next) + head.val # 子问题
        return s # 其他逻辑

1. 明确了终止条件，当head is None的时候就不需要再累加了，这个时候我们可以返回0
2. 提取重复逻辑，这里的重复逻辑也很简单，就是把当前的值与子问题的值累加即可self.listSum(head.next) + head.val

3. 数组求和

数组求和的递归是我自己瞎想的，主要是想要使用归并的思想，我们依然把原问题划分为子问题，进而缩小问题规模。但是这里我们需要调用两次子问题，我们把数组分为两个部分，然后分别求解出左边数组的和，右边数组的和，之后将其相加就是总的和

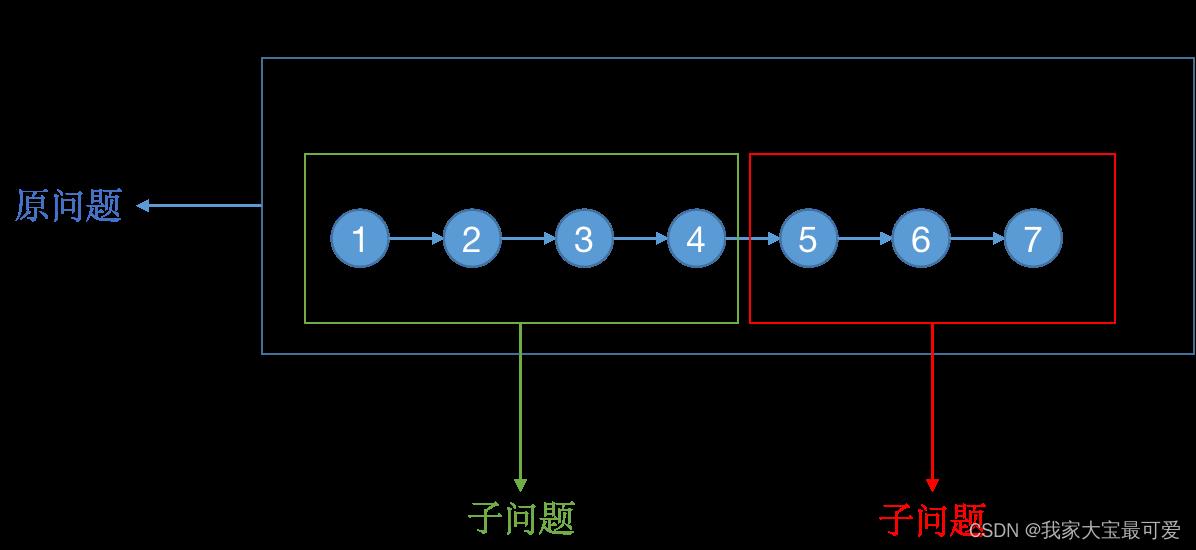
这个问题也很好的说明了递归的一个特点，那就是缩小问题规模，子问题与原问题是等价的，我们求解出子问题之后，需要再进行一些逻辑操作。现在突然想到一个问题，子问题与原问题等价吗？

1. 逻辑上肯定是相同的，只是问题规模缩小了。
2. 那些逻辑操作则是解决问题的

arr = [-1,2,3,4,5,6]

def mergeAdd(arr, l,r):
    if l >= r:
        return arr[l]
    
    m = (l + r) // 2

    lsum = mergeAdd(arr, l, m)
    rsum = mergeAdd(arr, m+1, r)

    return lsum + rsum

res = mergeAdd(arr,0,len(arr)-1)
print(res)

1. 终止条件，当左游标大于等于右游标的时候，说明只有一个元素了，此时直接返回值即可
2. 子问题和重复逻辑，原来求解的是0到len(arr)-1所有元素的和，现在求解成子问题0到m和子问题m+1到len(arr)-1和，调用了两次子问题，之后将求解的和相加即是总的和