22年多校第三场（F的证明

Posted 2022-08-06 吃花椒的妙酱

F题
题意：给定一个无向图，每次询问两点x, y，求是否存在一个n的排列，使得第一个元素为x，最后一个元素为y，且排列的任意一个前缀、任意一个后缀都连通。
解法
（发现还不会点双，赶紧入门了一下图论555
不难想到割点相关的东西，不过只是部分东西qaq
此题应该有点双性质入手
乱分类讨论一下
如果uv在同一点双，由点双性质，删任意点都能保持联通，所以直接yes。
如果uv在不同点双，且一共两个点双且相邻。（先不考虑不连通情况）。
也是可以构造排列$p_1{p}_2...pn$的，其中$p\mathrm{1..}pi$属于一个点双，$p_{i+1}...pn$属于另一个，$u=p_1,v=p_n$
如果有更多点双考虑怎么构造，用点双缩点后，是一棵树。因为uv必须在数组的头尾，这棵树必须是链的形式，uv所在的点双必须在链的头尾。结论感觉挺好想的。
反证法乱证下这棵树是条链：
假设不是链，那至少有三个叶子，设uv所在的点双分别为U,V(U≠V)，另一个叶子为T。不妨设U与T的lca为LCA，我们先将UV的路径构造到排列p中，
$p_1...p_i对应的是U->LCA这条路径上的点双$， $p_{i+1}...p_n对应的是U->LCA这条路径上的点双$，（省略处不代表是一串连续的下标）
此时还剩T->LCA这条路径上的点双没加入到排列中，考虑如果路径中只有T和LCA两个点，怎么去构造。
由于一个点可能同时属于多个点双，假设点双LCA中连接U，连接T的那个点（LCA,U,T是一个点集！）同时属于LCA,U和T（但是缩点的时候只能暂时被放在一个集合里，假设现在在LCA这个集合），因为这种情况能增加点双之间的连通性，从而更容易构造排列（表达能力不佳qaq），我们设这个关键点为k点。

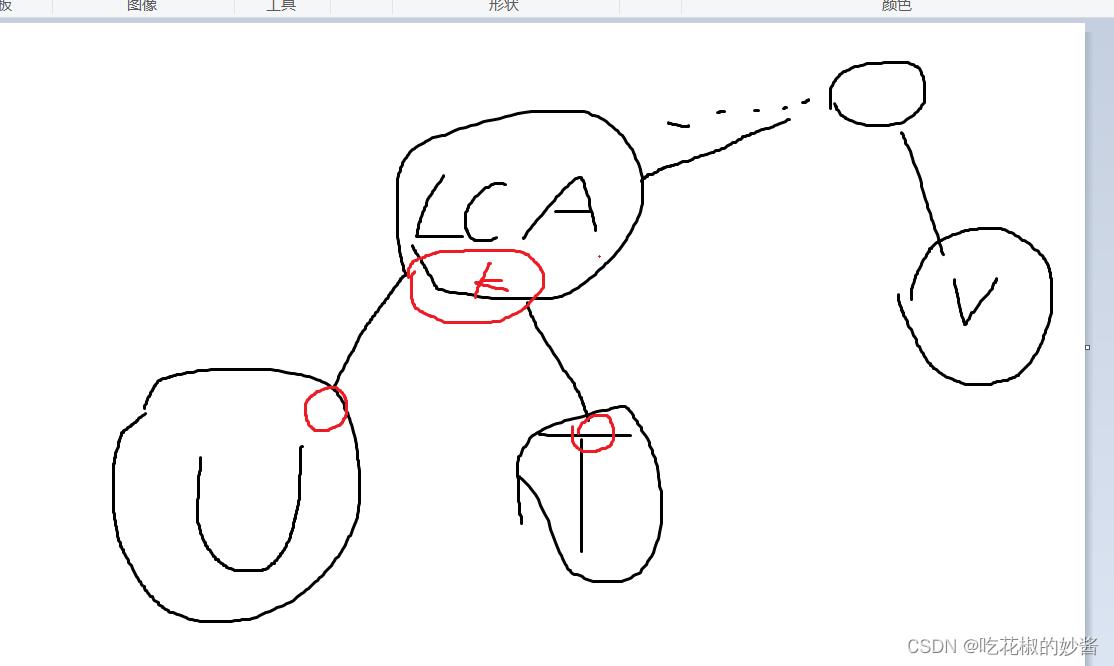
现在U到V这条路径已经安置在排列中了，考虑加入T。考虑让排列的前缀保持连通性，那一个最优方法就是加入k后，就去放T里的点，假设k后面接上一个T中的点q，我们再看排列后缀，此时后缀V到T条路径是不连通的，因为k在q前面！！！
那么推理到更坏情况更构造不出来了！
证毕

如果uv所在的点双在头尾的话，还要特判一下uv是割点的情况。毕竟以上只能保证构造出uv分离的排列，还要保证uv间的连通性。
注意特判n=2的情况，始终是yes。