系统的认识大数据人工智能数据分析中的数据

Posted 2022-08-05 肖永威

今天，大量数据、信息充斥我的日常生活和工作中，仿佛生活在数据和信息的海洋中，各类信息严重影响了我们的生活，碎片、垃圾、过时信息耗费了我们宝贵时间，最后可留在我们大脑中的数据、信息和知识少之又少，如何提高有效数据、信息转化率、加快知识积累，更高效的创新，成为我们数字化社会新课题。

数字化社会生活与企业构成如上图所示的金字塔模型，基础是数据，通过信息化、IoT、通讯等技术进行数字化；第二层是信息，通过流程上下文，数据驱动对数据处理；第三层是知识，对信息分类、分层次、归纳梳理；最后，顶端形成人工智能，实现决策支持。

随着数字经济发展，迎接未来的数字化生活，做为数字经济生活的基础数据，你了解多少，你认识大数据人工智能数据分析中的数据吗？有数字就是数字化吗？

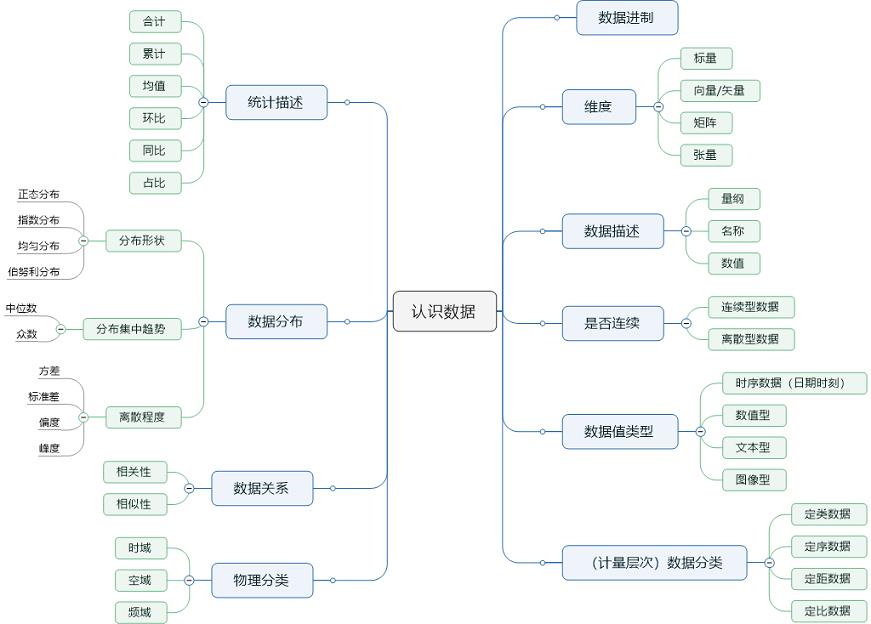
1. 数据维度

向量：既有大小又有方向的量，几何表示为有向线段，为向量，例如：力、位移、冲量等。

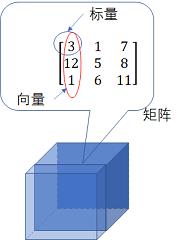
标量是0维的张量，向量是1维的张量，矩阵是二维的张量……除此之外，张量还可以是4维的、5维的。

2. 数据描述

2.1. 量纲

量纲是描述一个物理量，它由基本物理量组成的情况（所谓的“基本”，就是说这几个物理量之间是互相独立的），或者说，度量物理量单位的类别就叫做量纲。例如，速度的量纲就是长度除以时间，对应于国际单位制就是m/s 。

2.2. 单位

单位是衡量这个物理量的一种标准，也就是单位之间存在换算，例如 cm/s与m/s虽然都是速度的单位，它们不一样，存在换算。但是如果站在量纲的角度，它们的量纲是相同的，都是长度除以时间。

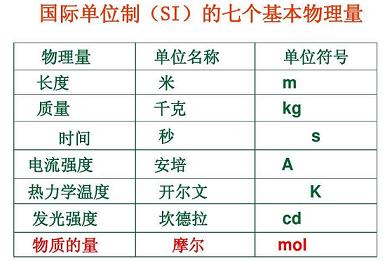
单位是用来描述量的大小、多少的，例如5m的长度，其中的1m就是单位，用来描述长度的大小，为了在全球引入标准的度量衡系统，国际计量大会（CGPM）采纳和推广了国际标准单位，其中就规定了7个基准单位（如下图）和基于这7个基准单位导出的导出单位。

2.3. 量纲分析

量纲分析就是寻找量纲之间的内在关系。物理方程不是量纲方程，但可以导出量纲方程。

3. 数据值类型

3.1. 时序数据（日期时刻）

2022年2月4日是北京冬季奥运会开幕的日子，与中国获得9枚金牌的数值对比，我们会发现，日期数据是没有大小可比较的，2月5日与4日无法比较，但是它们的差是24小时，这个时间是可以度量的。

虽然，2月5日与4日无法比较，但是它们可以表示时间顺序。

时间是人类主观概念的范畴，确切的说，应该是一个物理概念。如果要追寻本质，那就属于哲学范畴的问题。以物理学去理解“时间”这个概念，将毫无意义，因为这是主观概念已经定义的概念。我们所定义的时间概念，是自我相对存在的一个概念，而非本质复合的存在。

2022年2月4日，是24节气中的立春，是农历正月初四…，背后的数据内容很多，包括地点、温度、人数等等。

3.2. 数值型数据

数值型数据是数据分析中，基本可量化的数据表示。

3.3. 文本型数据

一般是描述人类语言的数据，不能直接被计算机所认知。

3.4. 图像数据

图像数据（Image Data）是指用数值表示的各像素（pixel）的灰度值的集合。

对真实世界的图像一般由图像上每一点光的强弱和频谱（颜色）来表示，把图像信息转换成数据信息时，须将图像分解为很多小区域，这些小区域称为像素，可以用一个数值来表示它的灰度，对于彩色图像常用红、绿、蓝三原色（trichromatic）分量表示。顺序地抽取每一个像素的信息，就可以用一个离散的阵列来代表一幅连续的图像。在地理信息系统中一般指栅格数据。

3.5. 音频数据

数字化的声音数据就是音频数据。

数字化声音的过程实际上就是以一定的频率对来自microphone 等设备的连续的模拟音频信号进行模数转换(ADC)得到音频数据的过程;数字化声音的播放就是将音频数据进行数模转换(DAC)变成模拟音频信号输出。在数字化声音时有两个重要的指标,即采样频率(Sampling Rate)和采样大小(SamplingSize)。

4. （计量层次）数据分类

按照数据的计量层次，可以将统计数据分为定类数据、定序数据、定距数据与定比数据。

4.1. 定类数据

这是数据的最低层。它将数据按照类别属性进行分类，各类别之间是平等并列关系。这种数据不带数量信息，并且不能在各类别间进行排序。例如，某商场将顾客所喜爱的服装颜色分为红色、白色、黄色等，红色、白色、黄色即为定类数据。又如，人类按性别分为男性和女性也属于定类数据。

虽然定类数据表现为类别，但为了便于统计处理，可以对不同的类别用不同的数字或编码来表示。如1表示女性，2表示男性，但这些数码不代表着这些数字可以区分大小或进行数学运算。不论用何种编码，其所包含的信息都没有任何损失。对定类数据执行的主要数值运算是计算每一类别中的项目的频数和频率。

4.2. 定序数据

这时数据的中间级别。定序数据不仅可以将数据分成不同的类别，而且各类别之间还可以通过排序来比较优劣。也就是说，定序数据与定类数据最主要的区别是定序数据之间还是可以比较顺序的。例如，人的受教育程度就属于定序数据。我们仍可以采用数字编码表示不同的类别：文盲半文盲=1，小学=2，初中-3，高中=4，大学=5，硕士=6，博士=7.通过将编码进行排序，可以明显地表示出受教育程度之间的高低差异。

虽然这种差异程度不能通过编码之间的差异进行准确的度量，但是可以确定其高低顺序，即可以通过编码数值进行不等式的运算。

4.3. 定距数据

定距数据是具有一定单位的实际测量值（如摄氏温度、考试成绩等）。此时不仅可以知道两个变量之间存在差异，还可以通过加、减法运算准确的计算出各变量之间的实际差距是多少。可以说，定距数据的精确性比定类数据和定序数据前进了一大步，它可以对事物类别或次序之间的实际距离进行测量。例如，甲的英语成绩为80分，乙的英语成绩为85分，可知乙的英语成绩比甲的高5分。

4.4. 定比数据

这是数据的最高等级。它的数据表现形式同定距数据一样，均为实际的测量值。定比数据与定距数据唯一的区别是：在定比数据中是存在绝对零点的，而定距数据中是不存在绝对零点的（零点是人为制定的）。因此定比数据间不仅可以比较大小，进行加、减运算，还可以进行乘、除运算。 [3]

5. 数据是否连续

离散数据（Discrete Data），即离散变量（Discrete Variables）。在统计学中，数据按变量值是否连续可分为连续数据与离散数据两种。

在一定区间内可以任意取值的数据叫连续数据，其数值是连续不断的，相邻两个数值可作无限分割，即可取无限个数值。例如，生产零件的规格尺寸和人体测量的身高和体重和胸围等为连续数据，其数值只能用测量或计量的方法获得。

6. 物理分类

6.1. 空间域

空间域（spatial domain）也叫空域，即所说的像素域，在空域的处理就是在像素级的处理，如在像素级的图像叠加。通过傅立叶变换后，得到的是图像的频谱。表示图像的能量梯度。

6.2. 频率域

频率域（frequency domain。）自变量是频率,即横轴是频率,纵轴是该频率信号的幅度,也就是通常说的频谱图。频谱图描述了信号的频率结构及频率与该频率信号幅度的关系。任何一个波形都可以分解成多个正弦波之和。每个正弦波都有自己的频率和振幅。所以任意一个波形信号有自己的频率和振幅的集合。频率域就是空间域经过傅立叶变换的信号

6.3. 时域

时域（时间域）——自变量是时间,即横轴是时间,纵轴是信号的变化。其动态信号x（t）是描述信号在不同时刻取值的函数。

7. 数据关系

7.1. 相关关系

当一个或几个相互联系的变量取一定的数值时，与之相对应的另一变量的值虽然不确定，但它仍按某种规律在一定的范围内变化。变量间的这种相互关系，称为具有不确定性的相关关系。

7.1.1. 按程度分类

• 完全相关：两个变量之间的关系，一个变量的数量变化由另一个变量的数量变化所惟一确定，即函数关系。
• 不完全相关：两个变量之间的关系介于不相关和完全相关之间。
• 不相关：如果两个变量彼此的数量变化互相独立，没有关系。

7.1.2. 按方向分类

• 正相关：两个变量的变化趋势相同，从散点图可以看出各点散布的位置是从左下角到右上角的区域，即一个变量的值由小变大时，另一个变量的值也由小变大。
• 负相关：两个变量的变化趋势相反，从散点图可以看出各点散布的位置是从左上角到右下角的区域，即一个变量的值由小变大时，另一个变量的值由大变小。

7.1.3. 按形式分类

• 线性相关（直线相关）：当相关关系的一个变量变动时，另一个变量也相应地发生均等的变动。
• 非线性相关（曲线相关）：当相关关系的一个变量变动时，另一个变量也相应地发生不均等的变动。

7.1.4. 按变量数目分类

• 单相关：只反映一个自变量和一个因变量的相关关系。
• 复相关：反映两个及两个以上的自变量同一个因变量的相关关系。
• 偏相关：当研究因变量与两个或多个自变量相关时，如果把其余的自变量看成不变（即当作常量），只研究因变量与其中一个自变量之间的相关关系，就称为偏相关。

7.2. 差异关系

差异研究的目的在于比较两组数据或多组数据之间的差异。差异关系中的差异是指不同样本组的某个指标的差异，例如男生和女生的智力差异，涉及到了变量的分组；相关分析是两个变量之间的关系，和样本分组无关，例如智力和学习成绩是否相关。

实际研究中有三种常见的差异性分析方法：T检验、方差分析、卡方检验。

7.3. 其他关系

• 集合结构：结构中的数据元素之间除了同属于一种类型外，别无其它关系。

• 树形结构：结构中的数据元素之间存在一对多的关系。

• 图状结构或是网状结构：结构中的数据元素之间存在多对多的关系。

以及数据的浓缩，聚类，权重计算，整体与部分关系等。

8. 数据分布

8.1. 分布集中趋势

中位数：对于倾斜（非对称）数据，数据中心的更好度量是中位数。中位数是有序数据值得中间值。它把数据较高的一半与较低的一半分开的值。

假定给定某属性X的N个值按递增排序，如果N是奇数，则中位数是该序集中的中间值；如果N是偶数，则中位数不唯一，它是最中间的两个值和它们之间的任意值。在X是数值属性的情况下，嘉定约定，中位数取做最中间两个值的平均值。

众数：众数是另一种中心趋势度量。数据集的整数是集合中出现最频繁的值。因此，可以对定性和定量属性确定众数。可能是最高频率对应多个不同值，导致多个众数。具有一个、两个、三个众数的数据集合分别称为单峰的，双峰的和三峰的。一般地，具有两个或更多众数的数据集是多峰的。在另一种极端的情况下，如果每个数据值仅出现一次，则它是没有众数的。

8.2. 数据离散程度

8.2.1. 极差

设某数值属性集合，极差位其最大值(max())与最小值(min())之差。

8.2.2. 分位数

假设属性X的数据以数值递增排序，想象我们可以挑选某些数据点，以便把数据分布划分成大小相等的连贯集。如图：

8.2.3. 四分位数

3个数据点，他们把数据分布划分成4个相等部分，使得每部分表示数据分布的四分之一。通常称为四分位数。

8.2.4. 方差和标准方差

方差和标准方差都是数据散布度量，他们指出数据分布的散布程度。低标准方差以为数据观察趋向于非常靠近均值，而高标准差表示数据散布在一个大的值域中。

（1）方差：
$${\sigma }^2=\frac{1}{2}\sum _{i=1}^n(x_i-\mu {)}^2$$
（2）标准差：
$$\sigma =\sqrt{\frac{1}{n-1}\sum _{i=1}^n(x_i-\mu {)}^2}$$
标准差是方差的开方，描述的是样本集合的各个样本点到均值的距离之平均；同时，也可以反映一个数据集的离散程度

8.2.5. 均值

$$\mu =\frac{1}{n}\sum _{i=1}^n{x}_i$$

8.3. 分布形状

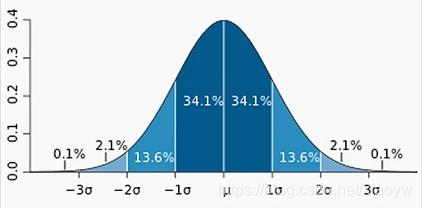
8.3.1. 正态分布

若随机变量$X$服从一个数学期望为$\mu$、方差为${\sigma }^2$的正态分布，记为$N(\mu ，{\sigma }^2)$。其概率密度函数为正态分布的期望值$\mu$决定了其位置，其标准差$\sigma$决定了分布的幅度。当$\mu =0,\sigma =1$时的正态分布是标准正态分布。

标准正态分布又称为$u$分布，是以0为均数、以1为标准差的正态分布，记为$N（0，1）$。

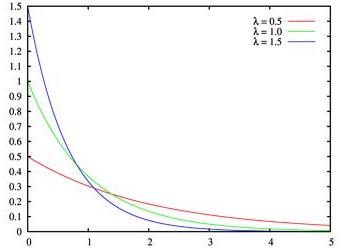
8.3.2. 指数分布

在概率理论和统计学中，指数分布（Exponential distribution也称为负指数分布）是描述泊松过程中的事件之间的时间的概率分布，即事件以恒定平均速率连续且独立地发生的过程。 这是伽马分布的一个特殊情况。 它是几何分布的连续模拟，它具有无记忆的关键性质。 除了用于分析泊松过程外，还可以在其他各种环境中找到。

$$f(x)=\begin{array}{cc}\lambda e^{-(\lambda x)}& ,x>0\\ 0& ,x\le 0\end{array}$$

在概率论和统计学中，指数分布是一种连续概率分布。指数分布可以用来表示独立随机事件发生的时间间隔，比如旅客进机场的时间间隔、中文维基百科新条目出现的时间间隔等等。

许多电子产品的寿命分布一般服从指数分布。有的系统的寿命分布也可用指数分布来近似。它在可靠性研究中是最常用的一种分布形式。指数分布是伽玛分布和威布尔分布的特殊情况，产品的失效是偶然失效时，其寿命服从指数分布。

期望与方差：
$E(X)=\frac{1}{\lambda }$
$Var(X)=\frac{1}{{\lambda }^2}$

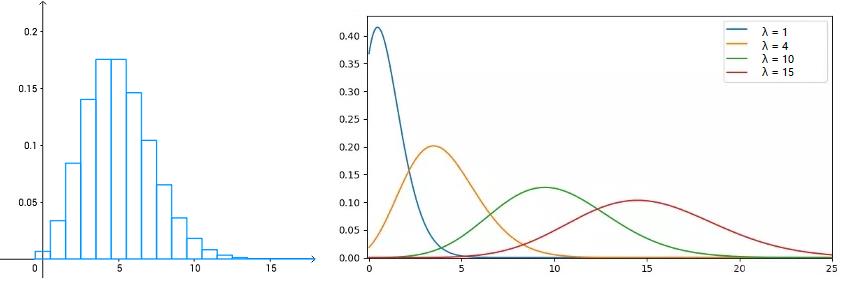
8.3.3. 泊松分布

泊松分布适合于描述单位时间内随机事件发生的次数的概率分布。如某一服务设施在一定时间内受到的服务请求的次数，电话交换机接到呼叫的次数、汽车站台的候客人数、机器出现的故障数、自然灾害发生的次数、DNA序列的变异数、放射性原子核的衰变数、激光的光子数分布等等。【维基百科】

$P(X=k)=\frac{{\lambda }^k}{k!}{e}^{-\lambda },k=0,1,...$

泊松分布的参数$\lambda$是单位时间(或单位面积)内随机事件的平均发生次数。 泊松分布适合于描述单位时间内随机事件发生的次数。
泊松分布的期望和方差均为$\lambda$

8.3.4. 二项分布

二项分布（binomial distrubution）就是重复n次独立的伯努利试验。在每次试验中只有两种可能的结果，而且两种结果发生与否互相对立，并且相互独立，与其它各次试验结果无关，事件发生与否的概率在每一次独立试验中都保持不变，则这一系列试验总称为n重伯努利实验，当试验次数为1时，二项分布服从0-1分布。

$$PX=k=\left(\genfrac{}{}{0ex}{}{n}{k}\right)p^k(1-p{)}^{(n-k)}$$

式中$k=0,1,2,...,n$，$\left(\genfrac{}{}{0ex}{}{n}{k}\right)=\frac{n!}{k!(n-k)!}$是二项式系数，又记为 C