NowCoderTOP17-22 二分查找/排序——持续更新ing

Posted 2022-08-05 王嘻嘻-

TOP17. 二分查找-I

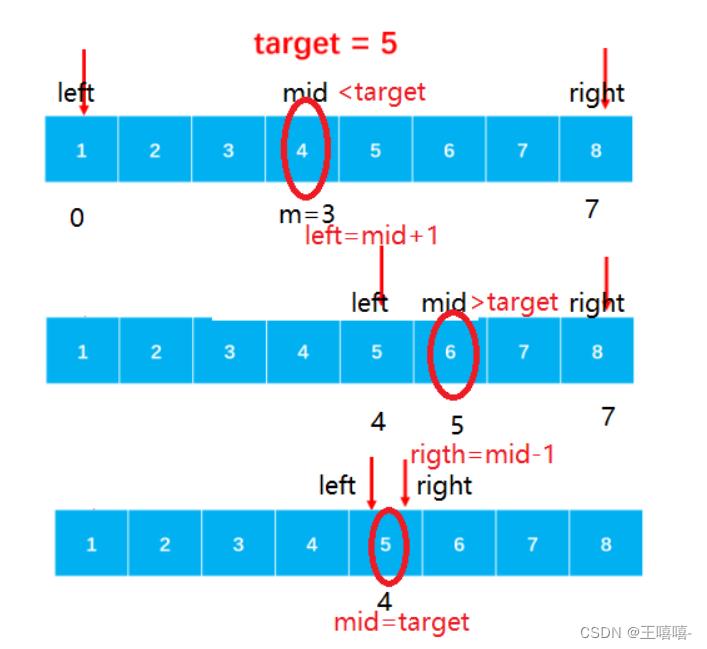
public class Solution 
    /**
     * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
     * @param nums int整型一维数组 
     * @param target int整型 
     * @return int整型
     */
    public int search (int[] nums, int target) 
        int l = 0;
        int r = nums.length - 1;
        while (l <= r) 
            int mid = (l + r) / 2;
            if(nums[mid] > target) 
                r = mid - 1;
            else if(nums[mid] < target)
                l = mid + 1;
            else if(nums[mid] == target)
                return mid;
            
        
        return -1;
    

TOP18. 二维数组里边的查找

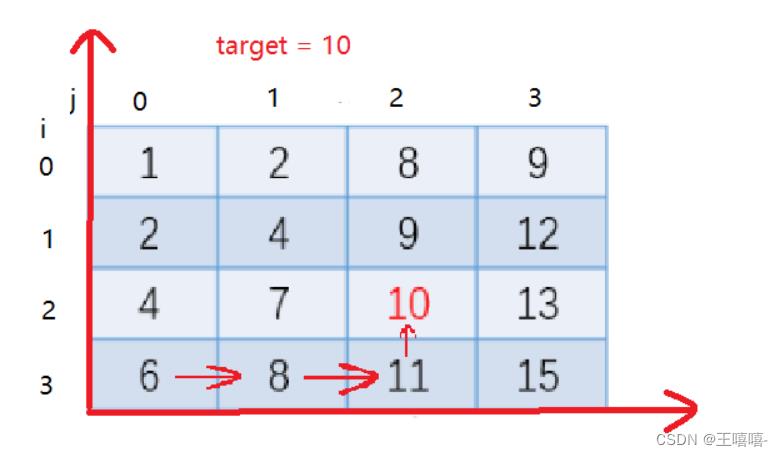
public class Solution 
    public boolean Find(int target, int [][] array) 
        // 边界条件
        if(array.length == 0 || array[0].length == 0) return false;
        // 默认从左下角开始遍历
        // 行下标
        int i = array.length - 1;
        // 列下标
        int j = 0;
        while(i >= 0 && j < array[0].length) 
            if(array[i][j] > target) --i;
            else if(array[i][j] < target) ++j;
            else return true;
        
        return false;
    

TOP19. 寻找峰值

public class Solution 
    /**
     * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
     * @param nums int整型一维数组 
     * @return int整型
     */
    public int findPeakElement (int[] nums) 
        int left = 0;
        int right = nums.length - 1;
        //二分法
        while(left < right)
            int mid = (left + right) / 2;
            //右边是往下，不一定有坡峰
            if(nums[mid] > nums[mid + 1])
                right = mid;
            //右边是往上，一定能找到波峰
            else
                left = mid + 1;
        
        //其中一个波峰
        return left;
    

TOP20. 数组中的逆序对

public class Solution 
    int count = 0;
    public int InversePairs(int [] array) 
        // 长度小于2则无逆序对
        if(array.length < 2) return 0;
        // 进入归并
        mergeSort(array, 0 ,array.length - 1);
        return count;
    
    
    public void mergeSort(int[] array, int left, int right) 
        // 找分割点
        int mid = left + (right - left) / 2;
        if(left < right) 
            // 左子树
            mergeSort(array, left, mid);
            //右子树
            mergeSort(array, mid + 1, right);
            // 合并
            Merge(array, left, right, mid);
        
    
    
    public void Merge(int[] array, int left, int right, int mid) 
        // 临时数组创建，长度为两个子数组加起来的长度
        int[] temp = new int[right - left + 1];
        // 临时数组的下标起点
        int newStart = 0;
        // 保存在原数组的起点下标值
        int oldStart = left;
        // 左子树的起始指针
        int l = left;
        // 右子树的起始指针
        int r = mid + 1;
        while(l <= mid && r <= right) 
            // 当左子数组的当前元素小的时候，跳过，无逆序对
            if(array[l] <= array[r]) 
                // 放入临时数组
                temp[newStart] = array[l];
                // 临时数组下标+1
                newStart ++;
                 // 左子数组指针右移
                l ++;
            else 
                // 存在逆序对
                // 放入临时数组
                temp[newStart] = array[r];
                 // 逆序对的个数为    左子数组的终点- 当前左子数组的当前指针
                count += mid + 1 - l;
                count %= 1000000007;
                // 临时数组+1
                newStart ++;
                // 右子数组的指针右移
                r++;
            
        
        // 右子树还有元素时，全部放入临时数组
        while(l <= mid) 
            temp[newStart++] = array[l++];
        
         // 左子树还有元素时，全部放入临时数组
        while(r <= right) 
            temp[newStart++] = array[r++];
        
        // 将临时数组中的元素放入到原数组的指定位置
        for(int num : temp) 
            array[oldStart++] = num;
        
    

TOP21. 旋转数组的最小数字

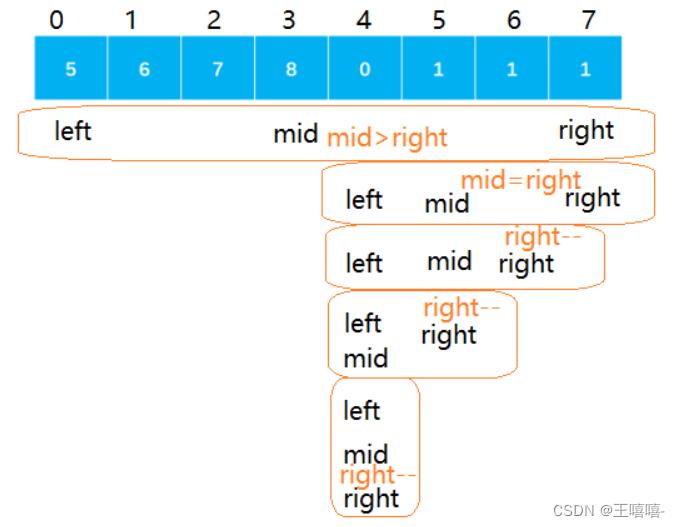
public class Solution 
    public int minNumberInRotateArray(int [] array) 
        // 二分查找
        int left = 0;
        int right = array.length - 1;
        while(left < right) 
        int mid = left + (right - left) / 2;
            if(array[mid] > array[right]) 
                left = mid + 1;
            else if(array[mid] == array[right]) 
                right--;
            else 
                right = mid;
            
        
        return array[right];
//         return array[left];
        
        
//         // 遍历查找
//         int temp = array[0];
//         for(int i = 0; i < array.length ; i++) 
//             if(array[i] < temp) 
//                 temp = array[i];
//             
//         
//         return temp;
    

TOP22. 比较版本号

public class Solution 
    /**
     * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
     * 比较版本号
     * @param version1 string字符串 
     * @param version2 string字符串 
     * @return int整型
     */
    public int compare (String version1, String version2) 
        int n1 = version1.length();
        int n2 = version2.length();
        int i = 0;
        int j = 0;
        // 直到某个字符串结束
        while(i < n1 || j < n2) 
            long num1 = 0;
            // 从下一个点前截取数字
            while(i < n1 && version1.charAt(i) != '.') 
                num1 = num1 * 10 + (version1.charAt(i) - '0');
                i++;
            
            // 跳过点
            i++;
            long num2 = 0;
            while(j < n2 && version2.charAt(j) != '.') 
                // charAt() 取出的是char字符 ！！！！
                num2 = num2 * 10 + (version2.charAt(j) - '0');
                j++;
            
            // 跳过点
            j++;
            // 此时存在两个数字，比较大小
            if(num1 > num2) 
                return 1;
            
            if(num1 < num2) 
                return -1;
            
        
        // 若版本号相同
        return 0;