Codeforces Round #375 (Div. 2)题解报告

Posted 2022-07-31 queuelovestack

此文章可以使用目录功能哟↑(点击上方[+])

终测C题被卡,居然是题目理解错了,我这英语水平也是够了...

链接→Codeforces Round #375 (Div. 2)

 Problem A-The New Year: Meeting Friends

Accept: 0    Submit: 0
Time Limit: 1 second    Memory Limit : 256 megabytes

 Problem Description

There are three friend living on the straight line Ox in Lineland. The first friend lives at the point x1, the second friend lives at the point x2, and the third friend lives at the point x3. They plan to celebrate the New Year together, so they need to meet at one point. What is the minimum total distance they have to travel in order to meet at some point and celebrate the New Year?

It's guaranteed that the optimal answer is always integer.

 Input

The first line of the input contains three distinct integers x1, x2 and x3 (1 ≤ x1, x2, x3 ≤ 100) — the coordinates of the houses of the first, the second and the third friends respectively.

 Output

Print one integer — the minimum total distance the friends need to travel in order to meet together.

 Sample Input

7 1 4
30 20 10

 Sample Output

6
20

 Hint

In the first sample, friends should meet at the point 4. Thus, the first friend has to travel the distance of 3 (from the point 7 to the point 4), the second friend also has to travel the distance of 3 (from the point 1 to the point 4), while the third friend should not go anywhere because he lives at the point 4.

 Problem Idea

解题思路:

【题意】

一维坐标轴上有三个点x1,x2,x3

让你确定一个点,使得三个点到该点的距离之和最小

输出该最小距离之和

【类型】
签到题,考查思维
【分析】

假设三个点x1,x2,x3到点x的距离之和为d,那么

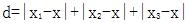
要使得d尽可能小,我们不妨分情况讨论一下,不过在分情况讨论之前,为了方便分析,我们先规定一下x3>x2>x1:

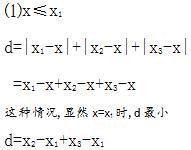
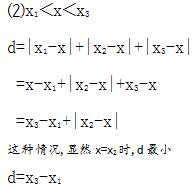
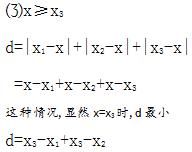
综上所述,当且仅当x=x2时,即取中间点作为目标点时,距离之和最小

【时间复杂度&&优化】
O(1)

题目链接→Codeforces Problem 723A The New Year: Meeting Friends

 Source Code

/*Sherlock and Watson and Adler*/
#pragma comment(linker, "/STACK:1024000000,1024000000")
#include<stdio.h>
#include<string.h>
#include<stdlib.h>
#include<queue>
#include<stack>
#include<math.h>
#include<vector>
#include<map>
#include<set>
#include<bitset>
#include<cmath>
#include<complex>
#include<string>
#include<algorithm>
#include<iostream>
#define eps 1e-9
#define LL long long
#define PI acos(-1.0)
#define bitnum(a) __builtin_popcount(a)
using namespace std;
const int N = 100005;
const int M = 100005;
const int inf = 1000000007;
const int mod = 101;
int s[3];
int main()

    int i;
    for(i=0;i<3;i++)
        scanf("%d",&s[i]);
    sort(s,s+3);
    printf("%d\\n",s[2]-s[0]);
    return 0;

 Problem B-Text Document Analysis

Accept: 0    Submit: 0
Time Limit: 1 second    Memory Limit : 256 megabytes

 Problem Description

Modern text editors usually show some information regarding the document being edited. For example, the number of words, the number of pages, or the number of characters.

In this problem you should implement the similar functionality.

You are given a string which only consists of:

• uppercase and lowercase English letters,
• underscore symbols (they are used as separators),
• parentheses (both opening and closing).

It is guaranteed that each opening parenthesis has a succeeding closing parenthesis. Similarly, each closing parentheses has a preceding opening parentheses matching it. For each pair of matching parentheses there are no other parenthesis between them. In other words, each parenthesis in the string belongs to a matching "opening-closing" pair, and such pairs can't be nested.

For example, the following string is valid: "_Hello_Vasya(and_Petya)__bye_(and_OK)".

Word is a maximal sequence of consecutive letters, i.e. such sequence that the first character to the left and the first character to the right of it is an underscore, a parenthesis, or it just does not exist. For example, the string above consists of seven words: "Hello", "Vasya", "and", "Petya", "bye", "and" and "OK". Write a program that finds:

• the length of the longest word outside the parentheses (print 0, if there is no word outside the parentheses),
• the number of words inside the parentheses (print 0, if there is no word inside the parentheses).

 Input

The first line of the input contains a single integer n (1 ≤ n ≤ 255) — the length of the given string. The second line contains the string consisting of only lowercase and uppercase English letters, parentheses and underscore symbols.

 Output

Print two space-separated integers:

• the length of the longest word outside the parentheses (print 0, if there is no word outside the parentheses),
• the number of words inside the parentheses (print 0, if there is no word inside the parentheses).

 Sample Input

37
_Hello_Vasya(and_Petya)__bye_(and_OK)
37
_a_(_b___c)__de_f(g_)__h__i(j_k_l)m__
27
(LoooonG)__shOrt__(LoooonG)
5
(___)

 Sample Output

5 4
2 6
5 2
0 0

 Hint

In the first sample, the words "Hello", "Vasya" and "bye" are outside any of the parentheses, and the words "and", "Petya", "and" and "OK" are inside. Note, that the word "and" is given twice and you should count it twice in the answer.

 Problem Idea

解题思路:

【题意】

给你一个仅有大小写字母、下划线、小括号(小括号不会嵌套)组成的字符串

问括号外单词的最大长度以及括号内单词的个数

单词的定义为仅有大小写字母组成

【类型】
模拟题
【分析】

这题只要按照题目要求处理一遍字符串就可以了

可以用flag标记当前位置是括号内还是括号外

在括号内时,可以用is_word标记是否遇到单词

其他的只要注意细节,一般都不会有问题

【时间复杂度&&优化】
O(strlen(s))

题目链接→Codeforces Problem 723B Text Document Analysis

 Source Code

/*Sherlock and Watson and Adler*/
#pragma comment(linker, "/STACK:1024000000,1024000000")
#include<stdio.h>
#include<string.h>
#include<stdlib.h>
#include<queue>
#include<stack>
#include<math.h>
#include<vector>
#include<map>
#include<set>
#include<bitset>
#include<cmath>
#include<complex>
#include<string>
#include<algorithm>
#include<iostream>
#define eps 1e-9
#define LL long long
#define PI acos(-1.0)
#define bitnum(a) __builtin_popcount(a)
using namespace std;
const int N = 300;
const int M = 100005;
const int inf = 1000000007;
const int mod = 101;
char s[N];
int main()

    int n,Max,ans,tmp,i;
    bool flag=true,is_word=false;
    scanf("%d",&n);
    scanf("%s",s);
    for(Max=tmp=ans=i=0;s[i]!='\\0';i++)
    
        if(s[i]>='A'&&s[i]<='Z'||s[i]>='a'&&s[i]<='z')
        
            if(flag)
                tmp++;
            else
                is_word=true;
            continue;
        
        if(flag)
        
            Max=max(Max,tmp);
            tmp=0;
        
        else
        
            if(is_word)
                ans++;
            is_word=false;
        
        if(s[i]=='(')
            flag=false;
        else if(s[i]==')')
            flag=true;
    
    if(flag)
    
        Max=max(Max,tmp);
        tmp=0;
    
    else
    
        if(is_word)
            ans++;
        is_word=false;
    
    printf("%d %d\\n",Max,ans);
    return 0;

 Problem C-Polycarp at the Radio

Accept: 0    Submit: 0
Time Limit: 2 seconds    Memory Limit : 256 megabytes

 Problem Description

Polycarp is a music editor at the radio station. He received a playlist for tomorrow, that can be represented as a sequence a1, a2, ..., an, where ai is a band, which performs the i-th song. Polycarp likes bands with the numbers from 1 to m, but he doesn't really like others.

We define as bj the number of songs the group j is going to perform tomorrow. Polycarp wants to change the playlist in such a way that the minimum among the numbers b1, b2, ..., bm will be as large as possible.

Find this maximum possible value of the minimum among the bj (1 ≤ j ≤ m), and the minimum number of changes in the playlist Polycarp needs to make to achieve it. One change in the playlist is a replacement of the performer of the i-th song with any other group.

 Input

The first line of the input contains two integers n and m (1 ≤ m ≤ n ≤ 2000).

The second line contains n integers a1, a2, ..., an (1 ≤ ai ≤ 10^9), where ai is the performer of the i-th song.

 Output

In the first line print two integers: the maximum possible value of the minimum among the bj (1 ≤ j ≤ m), where bj is the number of songs in the changed playlist performed by the j-th band, and the minimum number of changes in the playlist Polycarp needs to make.

In the second line print the changed playlist.

If there are multiple answers, print any of them.

 Sample Input

4 2
1 2 3 2
7 3
1 3 2 2 2 2 1
4 4
1000000000 100 7 1000000000

 Sample Output

2 1
1 2 1 2
2 1
1 3 3 2 2 2 1
1 4
1 2 3 4

 Hint

In the first sample, after Polycarp's changes the first band performs two songs (b1 = 2), and the second band also performs two songs (b2 = 2). Thus, the minimum of these values equals to 2. It is impossible to achieve a higher minimum value by any changes in the playlist.

In the second sample, after Polycarp's changes the first band performs two songs (b1 = 2), the second band performs three songs (b2 = 3), and the third band also performs two songs (b3 = 2). Thus, the best minimum value is 2.

 Problem Idea

解题思路:

【题意】

有一个序列a1,a2,…,an

现在定义bj表示数j在序列中出现的次数

问最小值bj(1≤j≤m)的最大可能值为多少,以及最少需要替换序列中的几个数

并输出替换之后的序列a1,a2,…,an

【类型】
贪心
【分析】

首先,我们需要理解的是何为最小值bj(1≤j≤m)的最大可能值

因为bj表示数j(1≤j≤m)在序列中出现的次数

而每个数出现的次数一开始是不一定的,这时候会存在一个最小值bj,即出现次数最少的那个数的出现次数

而这个最大可能值的含义是我们要替换一些数,使得出现次数最少的次数尽可能大

例如下面这组数据

6 5

1 2 2 345 2134 885

最开始bj(1≤j≤m)分别为

  j= 1 2 3 4 5

bj= 1 2 0 0 0

那此时bj最小值为0,为了使bj最小值尽可能大,我们需做如下替换:

2->3 345->4 2134->5

这样之后bj最小值为1,替换次数为3

由抽屉原理可知,bj最小值的最大可能值为n/m

而要使得bj(1≤j≤m)均达到n/m,那就必须将>m的数或是bj>n/m的数替换成bj<n/m的数

这就是贪心的过程

【时间复杂度&&优化】
O(N+M)

题目链接→Codeforces Problem 723C Polycarp at the Radio

 Source Code

/*Sherlock and Watson and Adler*/
#pragma comment(linker, "/STACK:1024000000,1024000000")
#include<stdio.h>
#include<string.h>
#include<stdlib.h>
#include<queue>
#include<stack>
#include<math.h>
#include<vector>
#include<map>
#include<set>
#include<bitset>
#include<cmath>
#include<complex>
#include<string>
#include<algorithm>
#include<iostream>
#define eps 1e-9
#define LL long long
#define PI acos(-1.0)
#define bitnum(a) __builtin_popcount(a)
using namespace std;
const int N = 2005;
const int M = 100005;
const int inf = 1000000007;
const int mod = 101;
int s[N],v[N];
int main()

    int n,m,i,j,k=0;
    scanf("%d%d",&n,&m);
    for(i=1;i<=n;i++)
    
        scanf("%d",&s[i]);
        if(s[i]<=m)
            v[s[i]]++;
    
    for(j=i=1;i<=n;i++)
    
        while(j<=m&&v[j]>=n/m)
            j++;
        if(j>m)
            break;
        if(s[i]>m||v[s[i]]>n/m)
        
            if(s[i]<=m)
                v[s[i]]--;
            s[i]=j,v[j]++,k++;
        
    
    printf("%d %d\\n",n/m,k);
    for(i=1;i<=n;i++)
        printf("%d%c",s[i],i!=n?' ':'\\n');
    return 0;

 Problem D-Lakes in Berland

Accept: 0    Submit: 0
Time Limit: 2 seconds    Memory Limit : 256 megabytes

 Problem Description

The map of Berland is a rectangle of the size n × m, which consists of cells of size 1 × 1. Each cell is either land or water. The map is surrounded by the ocean.

Lakes are the maximal regions of water cells, connected by sides, which are not connected with the ocean. Formally, lake is a set of water cells, such that it's possible to get from any cell of the set to any other without leaving the set and moving only to cells adjacent by the side, none of them is located on the border of the rectangle, and it's impossible to add one more water cell to the set such that it will be connected with any other cell.

You task is to fill up with the earth the minimum number of water cells so that there will be exactly k lakes in Berland. Note that the initial number of lakes on the map is not less than k.

 Input

The first line of the input contains three integers n, m and k (1 ≤ n, m ≤ 50, 0 ≤ k ≤ 50) — the sizes of the map and the number of lakes which should be left on the map.

The next n lines contain m characters each — the description of the map. Each of the characters is either '.' (it means that the corresponding cell is water) or '*' (it means that the corresponding cell is land).

It is guaranteed that the map contain at least k lakes.

 Output

In the first line print the minimum number of cells which should be transformed from water to land.

In the next n lines print m symbols — the map after the changes. The format must strictly follow the format of the map in the input data (there is no need to print the size of the map). If there are several answers, print any of them.

It is guaranteed that the answer exists on the given data.

 Sample Input

5 4 1
****
*..*
****
**.*
..**
3 3 0
***
*.*
***

 Sample Output

1
****
*..*
****
****
..**
1
***
***
***

 Hint

In the first example there are only two lakes — the first consists of the cells (2, 2) and (2, 3), the second consists of the cell (4, 3). It is profitable to cover the second lake because it is smaller. Pay attention that the area of water in the lower left corner is not a lake because this area share a border with the ocean.

 Problem Idea

解题思路:

【题意】

n*m的矩形,每个格子不是'*'就是'.','*'代表陆地,'.'代表水

定义湖是有多个相邻的水组成的(且湖周围必须是陆地,故与海洋相连的水不能组成湖)

问至少要填补多少个单位的水,才能使得恰好有k个湖

【类型】
模拟+dfs
【分析】

假设最初n*m的矩形中有t个湖

总体来说,出题人还算是人性化的,他的一句话把本题的难度降低了

"Note that the initial number of lakes on the map is not less than k." => t≥k

这句话意味着我们只要将湖面积较小的t-k个湖完全填掉就可以了

而不用填某些格子,使得一个湖分成多个湖

那么我们需要做的是先一遍dfs将湖的个数找出来,当然,要排除那些与海洋相连接的水

然后将找出的湖丢进优先队列中,按湖面积从小到大排列

接着就是填补优先队列中前t-k个湖即可

【时间复杂度&&优化】
O(N×M)

题目链接→Codeforces Problem 723D Lakes in Berland

 Source Code

/*Sherlock and Watson and Adler*/
#pragma comment(linker, "/STACK:1024000000,1024000000")
#include<stdio.h>
#include<string.h>
#include<stdlib.h>
#include<queue>
#include<stack>
#include<math.h>
#include<vector>
#include<map>
#include<set>
#include<bitset>
#include<cmath>
#include<complex>
#include<string>
#include<algorithm>
#include<iostream>
#define eps 1e-9
#define LL long long
#define PI acos(-1.0)
#define bitnum(a) __builtin_popcount(a)
using namespace std;
const int N = 55;
const int M = 100005;
const int inf = 1000000007;
const int mod = 101;
char s[N][N];
bool v[N][N],flag;
int ans,n,m,c,g[4][2]=0,1,1,0,-1,0,0,-1;
struct node

    int x,y,num;
    node()
    node(int _x,int _y,int _num):x(_x),y(_y),num(_num)
    bool operator < (const node &a) const
    
       return num>a.num;//最小值优先
    
;
priority_queue<node> q;
void dfs1(int x,int y)

    ans++;
    v[x][y]=true;
    for(int i=0;i<4;i++)
    
        int l=x+g[i][0];
        int r=y+g[i][1];
        if(!v[l][r]&&s[l][r]=='.')
        
            if(!l||!r||l==n-1||r==m-1)
            
                flag=false;
                continue;
            
            dfs1(l,r);
        
    

void dfs2(int x,int y)

    v[x][y]=true;
    s[x][y]='*';
    c++;
    for(int i=0;i<4;i++)
    
        int l=x+g[i][0];
        int r=y+g[i][1];
        if(!v[l][r]&&s[l][r]=='.')
            dfs2(l,r);
    

int main()

    int k,i,j,t=0;
    node u;
    memset(v,false,sizeof(v));
    scanf("%d%d%d",&n,&m,&k);
    for(i=0;i<n;i++)
        scanf("%s",s[i]);
    for(i=1;i<n-1;i++)
        for(j=1;j<m-1;j++)
        
            if(s[i][j]=='.'&&!v[i][j])
            
                ans=0;
                flag=true;
                dfs1(i,j);
                if(flag)
                
                    t++;
                    q.push(node(i,j,ans));
                
            
        
    c=0;
    memset(v,false,sizeof(v));
    while(t>k)
    
        u=q.top();
        q.pop();
        dfs2(u.x,u.y);
        t--;
    
    printf("%d\\n",c);
    for(i=0;i<n;i++)
        printf("%s\\n",s[i]);
    return 0;

菜鸟成长记