校招实习笔面试实战，LeetCode分割字符串常考题目，图文解析

Posted 2022-07-28 陆海潘江小C

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了校招实习笔面试实战，LeetCode分割字符串常考题目，图文解析相关的知识，希望对你有一定的参考价值。

校招实习实战，LeetCode分割字符串常考题目，图文解析

1 分割字符串(动态规划+回溯)
2 分割字符串II(两次动态规划)

备战春招，校招实习笔试面试经验分享，拿Java开发工程师offer~~

本系列文章包括Java、算法、计算机网络、数据库、操作系统等等，本篇介绍面试【Java工程师】岗位笔试面试中常考的算法题目，分析解题思路。

传送门：

【亲身面经分享，校招实习面试系列】每日10题，快速学习（Java基础篇）
【校招实习面试系列，每日10题，快速学习】Java高级篇
【校招实习面试系列】你知道网络中4类IO模型是什么吗？我的朋友如此优秀回答
【校招实习面试实战，身临其境】华为软件开发工程师面试复盘总结
校招实习面试实战，顺丰科技Java工程师面试复盘总结

我们都知道，校招实习的面试之前，需要进行笔试，主要是进行一轮筛选，很多公司都会给所有投简历的同学发笔试通知，我们可以当作练练手。

不过，笔试成绩重不重要每个公司都有不一样的对待，比如华为的机试，据说成绩100+就有面试机会，这个还是不难的，只要做出第一道题就有100分，剩下两道题尽力就好。还有字节跳动，一想到笔试就很难，喜欢考算法，不过笔试成绩倒不是很重要，只要你的简历很不错他们看中了，就有机会。

说了这么多，我们当然希望笔试的题目能做好，毕竟好的成绩还是很有绝对优势的，说明你的编程能力、算法能力不错！

而且，在每一轮面试中，大多数面试官还是会让你手撕代码，这就直接决定面试评价了。

这篇我们就来看看，笔试面试中常考的题目，LeetCode分割字符串，属于算法题目中的动态规划和回溯，下面看看如何简单解决问题，面试之路所向披靡！

1 分割字符串(动态规划+回溯)

先看看题目，寥寥几字，是一道中等难度的算法题。

给你一个字符串 s，请你将 s 分割成一些子串，使每个子串都是回文串。返回 s 所有可能的分割方案。

回文串 是正着读和反着读都一样的字符串。

示例 1：

输入：s = “aab”
输出：[[“a”,“a”,“b”],[“aa”,“b”]]

示例 2：

输入：s = “a”
输出：[[“a”]]

提示：

1 <= s.length <= 16
s 仅由小写英文字母组成

链接：https://leetcode-cn.com/problems/palindrome-partitioning/

拿到题目后，首先仔细阅读内容，这一点很重要，指导了你的思路往哪个方向，关系到用什么方法解决问题。

所以，除非很熟练，拿到题目就直接写代码可能会出错，遗漏边界情况等细节问题。

我们来看题目内容，“所有可能的分割方案”则是一个重点提示，说明要使用枚举、回溯递归来保存所有结果。

整体阅读题目，要找到字符串s中的所有回文串，而且s的长度是1 <= s.length <= 16，就可以确定要使用回溯的思想解决问题了。

现在还有一个问题，如何确定s中的子串是回文串呢？

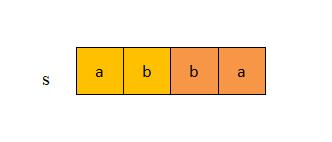
如上图，s=“abba”，容易看出，s中包含的回文串有"a",“b”,“bb”,abba".

如何编程实现这种识别回文串是接下来第一个要解决的问题。

回到题目中**“回文串”**的定义：回文串 是正着读和反着读都一样的字符串。

因此，可以假设s(i,j)表示字符串s中i到j的子串，f[i][j]是标记这个子串s(i,j)是否为回文串的标记，这就初步实现了问题的转化。

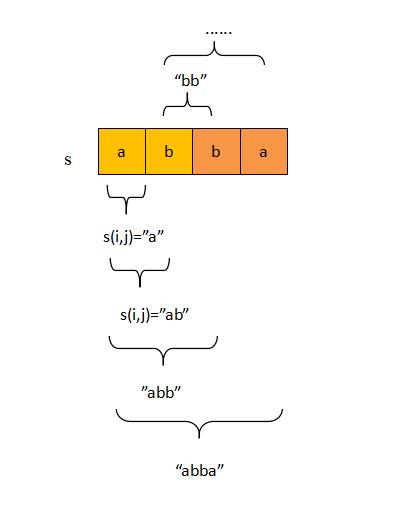
观察一下上图，一个字符串是回文串的特点可以总结为两点：

头尾字符一样。s[i]==s[j].
除去头尾字符，中间的串必须也是回文串。s(i+1)(j-1)是回文串，即f[i][j]=true.

同时满足以上两个条件，可以确定是回文串。

到这里，思路打开了不止一点，可以用动态规划来写代码实现这个回文串识别功能了。

public List<List<String>> partition(String s) 
    int len = s.length();
    f = new boolean[len][len];//输入的字符串s中，子串s(i,j)是回文串,f[i][j]=true,否则，f[i][j]=false.

    //动态规划，如果子串s(i,j)是回文串，则s[i]==s[j] && s(i+1,j-1).
    //就是满足回文串的条件：字符串头尾字符一样，而且出去头尾字符的中间字符串也应该是回文串.
    //所以，按照这个方法，i需要从大到小，j从小到大进行检测.
    for (int j = 0; j < len; j++) 
        for (int i = j; i >= 0; i--) 
            //头尾相等标记
            boolean flag = s.charAt(i) == s.charAt(j);
            //"aba","a"
            if (j - i <= 2) 
                f[i][j] = flag;
             else //"abca","abba"
                f[i][j] = flag && f[i + 1][j - 1];

实现起来，看代码也是很清晰。

剩下的就是将字符串s通过不同分割方案，得到的所有回文串的结果。上面讲到这里使用回溯的算法思想实现，具体是递归的编程方法。

回溯的模板大致是这样的：

public void backtrack(...,path,res) 
    if (达到结束条件) 
        res.add(path);//深度拷贝
        return;
    
    for (int i = ...; i < ...; i++) 
        if (符合选择要求) 
            path.add(当前选择);
            backtrack(..., path, res);
            path.remove(最后一个选择);//清除状态，不影响下一轮

所以，问题得到解决了，完整的代码如下：

import java.util.ArrayList;
import java.util.List;

public class palindrome_partitioning_131 

    List<List<String>> res = new ArrayList<>();//存放所有结果
    List<String> path = new ArrayList<>();//存放一条结果
    boolean[][] f;//标记输入的字符串s中，子串s(i,j)是否是回文串

    /**
     * @param s 输入的字符串
     * @return 返回所有回文串的列表
     * @author Charzous
     * @date 2022-03-29
     */
    public List<List<String>> partition(String s) 
        int len = s.length();
        f = new boolean[len][len];

        //动态规划，如果子串s(i,j)是回文串，则s[i]==s[j] && s(i+1,j-1)
        //就是满足回文串的条件：字符串头尾字符一样，而且出去头尾字符的中间字符串也应该是回文串
        //所以，按照这个方法，i需要从大到小，j从小到大进行检测
        for (int j = 0; j < len; j++) 
            for (int i = j; i >= 0; i--) 
                //头尾相等标记
                boolean flag = s.charAt(i) == s.charAt(j);
                //"aba","a"
                if (j - i <= 2) 
                    f[i][j] = flag;
                 else //"abca","abba"
                    f[i][j] = flag && f[i + 1][j - 1];
                
            
        

        backtrack(s, 0, f, path, res);
        return res;

    
    /**
     * @param s    输入的字符串
     * @param idx  本轮递归开始的下标
     * @param f    标记回文串的矩阵
     * @param path 存放一条回文串结果
     * @param res  存放全部回文子串结果
     * @author Charzous
     * @date 2022-03-29
     *
     */
    public void backtrack(String s, int idx, boolean[][] f, List<String> path, List<List<String>> res) 
        if (idx == s.length()) 
            res.add(new ArrayList<>(path));
            return;
        
        for (int i = idx; i < s.length(); i++) 
            //如果是回文串
            if (f[idx][i]) 
                //截取之后作为一个结果
                path.add(s.substring(idx, i + 1));
                backtrack(s, i + 1, f, path, res);
                path.remove(path.size() - 1);
            
        
    

    public static void main(String[] args) 
        palindrome_partitioning_131 solution = new palindrome_partitioning_131();
        String s = "aabccbabc";
        List<List<String>> res = solution.partition(s);
        for (List<String> list : res) 
            System.out.println(list);

测试s=“aabccbabc”，结果输出如下：

2 分割字符串II(两次动态规划)

这是第一题的升级版，属于困难等级，题目字数依然不多，所以每个字都显得很重要。

给你一个字符串 s，请你将 s 分割成一些子串，使每个子串都是回文。

返回符合要求的 最少分割次数 。

示例 1：

输入：s = “aab”
输出：1
解释：只需一次分割就可将 s 分割成 [“aa”,“b”] 这样两个回文子串。
示例 2：

输入：s = “a”
输出：0
示例 3：

输入：s = “ab”
输出：1

提示：

1 <= s.length <= 2000
s 仅由小写英文字母组成

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/palindrome-partitioning-ii
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

阅读题目之后，发现有一些区别，这次是对字符串s进行分割，希望使用最少次数让所有子串都是回文串。

也有相似之处，都是要求分割后的子串是回文串，所以识别回文串使用相同的方法。

最少分割次数是一个关键点，s的长度1 <= s.length <= 2000也是如此，推测出需要使用动态规划完成这道题目。

总体来说，需要通过两次动态规划，第一次识别子串是回文串，第二次找出一个方案，这个方案的分割次数最少。

重点就是第二个动态规划了，因为第一个方法在上面已经实现！

也就是我们现在已经拿到矩阵f[i][j]，要借助它找到最少分割次数的方案。

这里用一个count数组，count[i]表示子串s(j,i)分割为回文串的最少次数，当i==s.length()，计算得到s(0,i)时，count[s.length()-1]就是字符串s的最少次数。

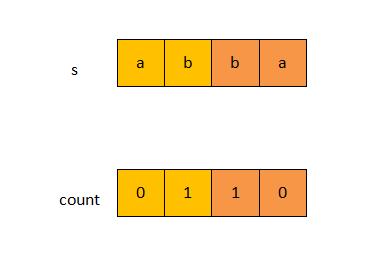
看了上面这个图，可以总结出动态规划的状态转移公式：

s(0,i)如果是回文串，即f[0][i]=true，那么count[i]=0
其他情况，s(i,j)就需要根据已有前面的分割次数，来确定当前位置i的最少次数。

具体实现可能看代码更清晰：

public int minCut(String s) 
    boolean[][] f = partition(s);
    int[] count = new int[s.length()];

    Arrays.fill(count, Integer.MAX_VALUE);
    for (int i = 0; i < s.length(); i++) 
        if (f[0][i])
            count[i] = 0;
        else 
            //遍历s(0,i)子串中每个分割点，找到最小的
            for (int j = 0; j < i; j++) 
                if (f[j + 1][i])//从i的下一个位置开始，识别为回文串的位置，记录最小次数
                    count[i] = Math.min(count[i], count[j] + 1);
            
        
    
    return count[s.length() - 1];

动态规划的思想就是找到从局部最优解到全局最优的状态转移公式。

这个题目的全部代码：

import java.util.Arrays;

public class palindrome_partitioning_ii_132 

    /**
     * @param s 输入的字符串
     * @return 返回所有回文串的列表
     * @author Charzous
     * @date 2022-03-29
     */
    public boolean[][] partition(String s) 
        int len = s.length();

        boolean[][] f = new boolean[len][len];//标记输入的字符串s中，子串s(i,j)是否是回文串

        //动态规划，如果子串s(i,j)是回文串，则s[i]==s[j] && s(i+1,j-1)
        //就是满足回文串的条件：字符串头尾字符一样，而且出去头尾字符的中间字符串也应该是回文串
        //所以，按照这个方法，i需要从大到小，j从小到大进行检测
        for (int j = 0; j < len; j++) 
            for (int i = j; i >= 0; i--) 
                //头尾相等标记
                boolean flag = s.charAt(i) == s.charAt(j);
                //"aba","a"
                if (j - i <= 2) 
                    f[i][j] = flag;
                 else //"abca","abba"
                    f[i][j] = flag && f[i + 1][j - 1];
                
            
        
        return f;
    

    public int minCut(String s) 
        boolean[][] f = partition(s);
        int[] count = new int[s.length()];

        Arrays.fill(count, Integer.MAX_VALUE);
        for (int i = 0; i < s.length(); i++) 
            if (f[0][i])
                count[i] = 0;
            else 
                //遍历s(0,i)子串中每个分割点，找到最小的
                for (int j = 0; j < i; j++) 
                    if (f[j + 1][i])//从i的下一个位置开始，识别为回文串的位置，记录最小次数
                        count[i] = Math.min(count[i], count[j] + 1);
                
            
        
        return count[s.length() - 1];
    

    public static void main(String[] args) 
        palindrome_partitioning_ii_132 solution = new palindrome_partitioning_ii_132();

        String s = "abbcabcc";
        int minCount = solution.minCut(s);
        System.out.println(minCount);