CEC2017基础函数说明Python版本
Posted Huterox
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了CEC2017基础函数说明Python版本相关的知识,希望对你有一定的参考价值。
文章目录
- 前言
- Bent Cigar Function
- Sum of Different Power Function
- Zakharov Function
- Rosenbrock’s Function
- Rastrigin’s Function
- Expanded Schaffer’s F6 Function
- Lunacek bi-Rastrigin Function
- Non-continuous Rotated Rastrigin’s Function
- Levy Function
- Modified Schwefel’s Function
- High Conditioned Elliptic Function
- Discus Function
- Ackley’s Function
- Weierstrass Function
- Griewank’s Function
- Katsuura Function
- HappyCat Function
- HGBat Function
- Schaffer's F7 Function
- 完整代码
前言
撑得慌,拿来练练手。部分函数没有实现,因为比较麻烦。我这边玩的话,也是直接拿这个玩,因为实际上他们玩的时候因该是加了偏置转换的,像cec2003好像都是没有偏置的。反正都能够说明问题,管你那么多。
Bent Cigar Function
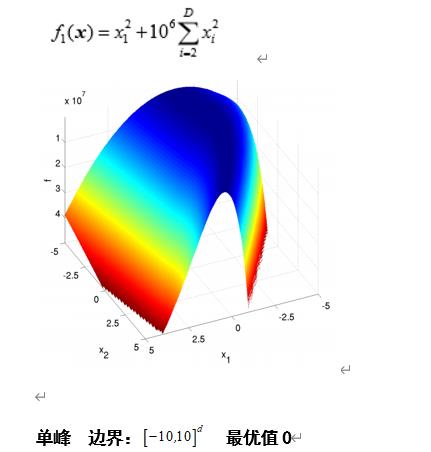
def F1(self,X):
Dim = len(X)
res = X[0]*X[0]
temp = 0.
for i in range(2,Dim+1):
temp+=X[i-1]*X[i-1]
res+=self.pow(10,6)*temp
return res
Sum of Different Power Function
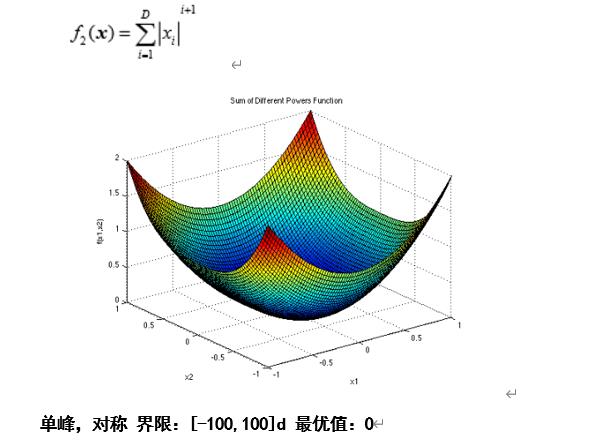
def F2(self,X):
res = 0.
Dim = len(X)
for i in range(1,Dim+1):
res+=self.pow(abs(X[i-1]),(i+1))
return res
Zakharov Function
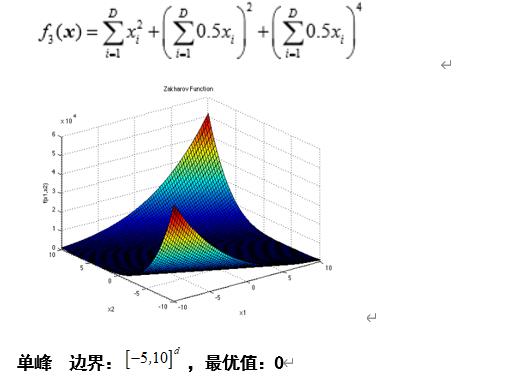
def F3(self,X):
part1 = 0.
part2 = 0.
for x in X:
part1+=x*x
part2+=0.5*x
res = part1+self.pow(part2,2)+self.pow(part2,4)
return res
Rosenbrock’s Function
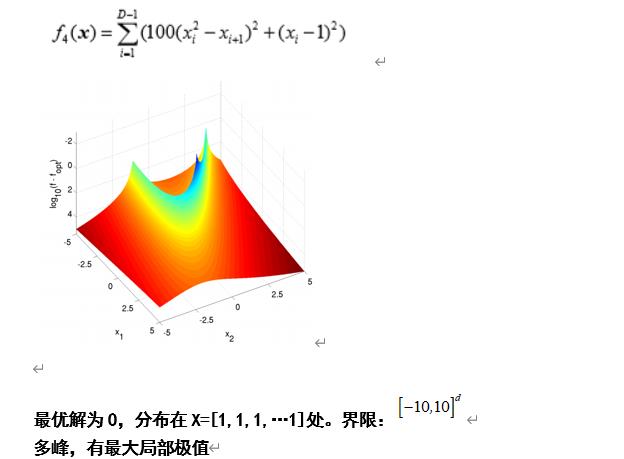
def F4(self,X):
Dim = len(X)
res = 0.
for i in range(1,Dim):
res+=100*self.pow((self.pow(X[i-1],2)-X[i]),2)+(X[i-1]-1)+self.pow((X[i]-1),2)
return res
Rastrigin’s Function
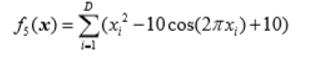
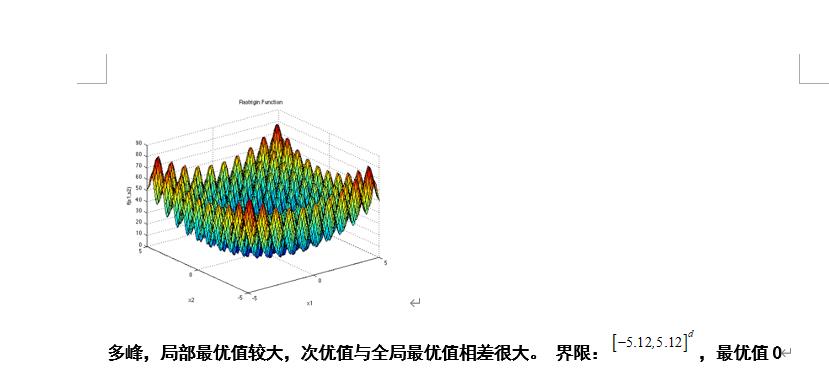
def F5(self,X):
res = 0.
for x in X:
res+=(x*x-10*self.cos(2*self.pi*x)+10)
return res
Expanded Schaffer’s F6 Function
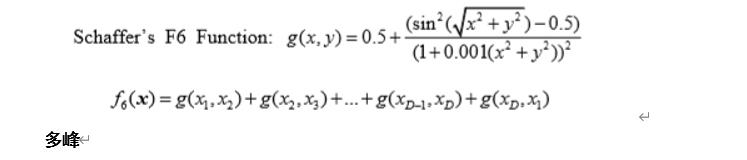
def __g(self,x1,x2):
res = 0.5+(self.pow(self.sin(self.sqrt(x1*x1+x2*x2)),2)/self.pow((1+0.001*(x1*x1+x2*x2)),2))
return res
def F6(self,X):
Dim = len(X)
res = 0.
for i in range(Dim-1):
res+=self.__g(X[i],X[i+1])
res+=self.__g(X[Dim-1],X[0])
return res
Lunacek bi-Rastrigin Function
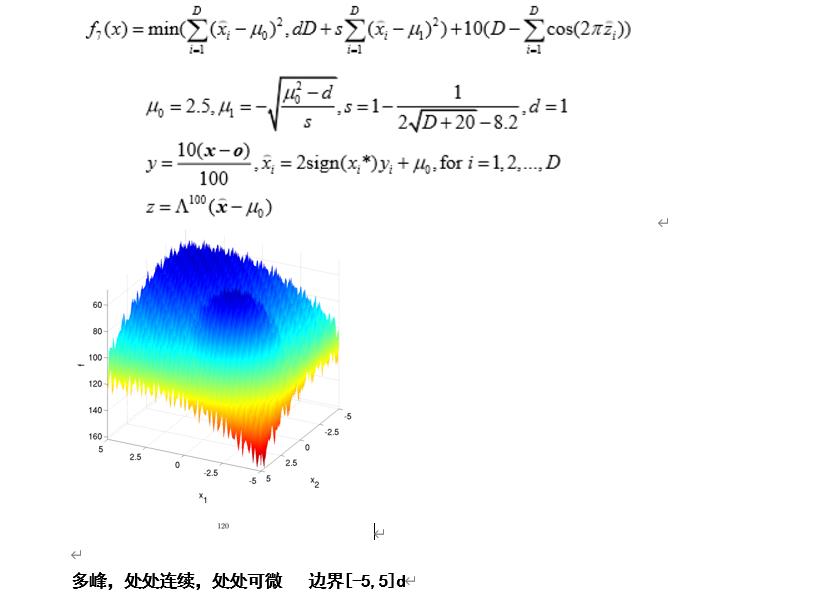
Non-continuous Rotated Rastrigin’s Function

def F8(self,X):
res = 0.
for x in X:
if(abs(x)<0.5):
y = x
else:
y = (round(2*x)/2)
res+=y*y - 10*(self.cos(2*self.pi*y)) + 10
return res
Levy Function
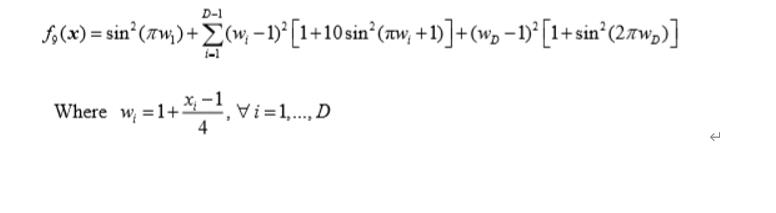
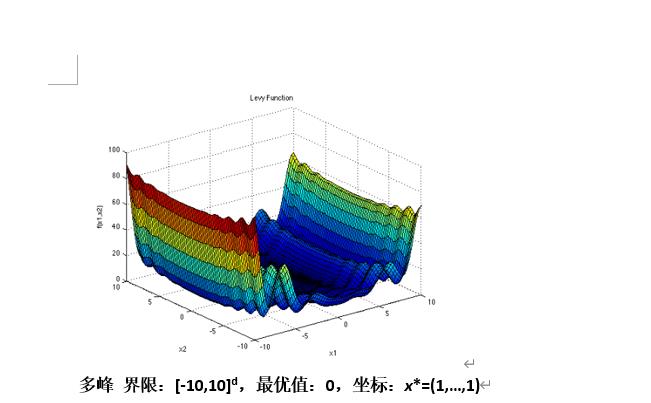
def F9(self,X):
Dim = len(X)
res = self.pow(self.sin(self.pi*(1+(X[0]-1/4))),2)
part2 = 0.
for i in range(1,Dim):
w = (1+(X[i-1]-1/4))
part2+=self.pow(w,2)*(1+10*self.pow(self.pi*w+1,2))
w = (1 + (X[Dim - 1] - 1 / 4))
res+=part2+(self.pow(w-1,2)*(1+self.pow(self.sin(2*self.pi*w),2)))
return res
Modified Schwefel’s Function

High Conditioned Elliptic Function
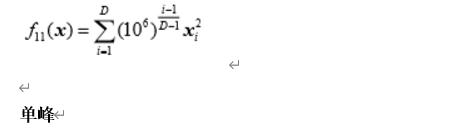
def F11(self,X):
Dim = len(X)
res = 0.
for i in range(1,Dim+1):
res+=self.pow(1000000,(i-1/Dim-1))*X[i-1]*X[i-1]
return res
Discus Function
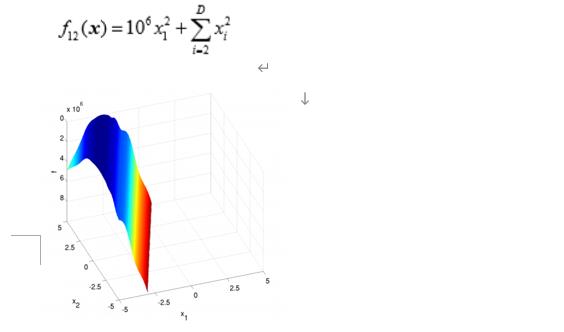
def F12(self,X):
res = 1000000*X[0]*X[0]
Dim = len(X)
for i in range(1,Dim):
res+=X[i]*X[i]
return res
Ackley’s Function
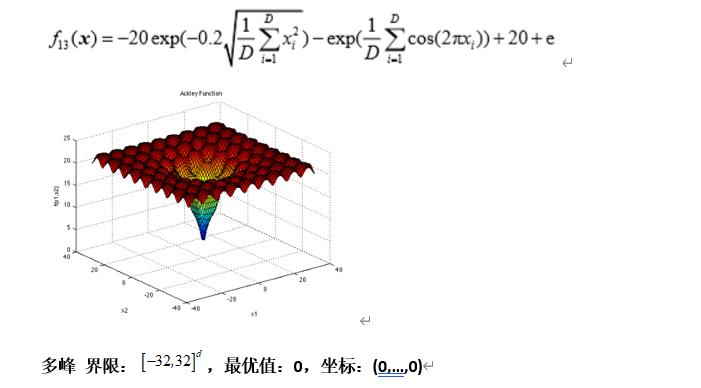
def F13(self,X):
Dim = len(X)
part2 = 0.
part3 = 0.
for x in X:
part2+=x*x
part3+=self.cos(self.pi*2*x)
res = -20*self.exp(-0.2*self.sqrt((1/Dim)*part2))-self.exp((1/Dim)*part3)+20+self.e
return res
Weierstrass Function
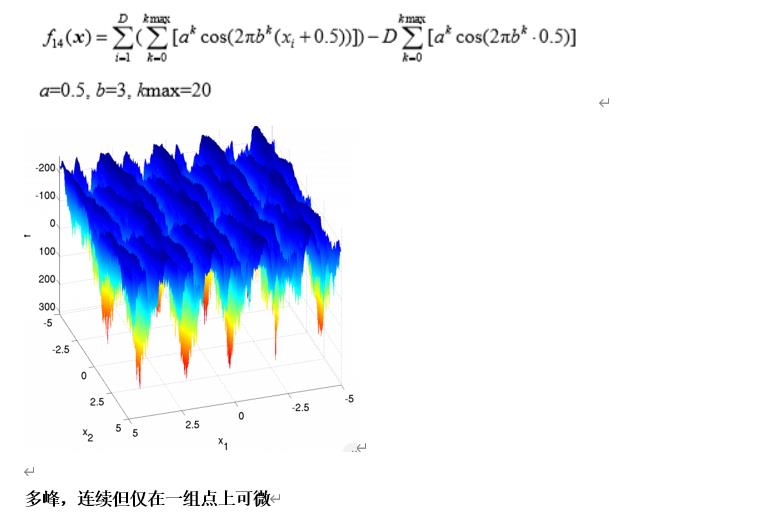
def F14(self,X):
kmax = 20;a=0.5;b=3
Dim = len(X)
part1 = 0.
for x in X:
temp = 0.
for i in range(kmax+1):
temp+=self.pow(a,i)*self.cos(2*self.pi*self.pow(b,i)*(x+0.5))
part1+=temp
part2 = Dim
temp=0.
for i in range(kmax+1):
temp += self.pow(a, i) * self.cos(2 * self.pi * self.pow(b, i) * 0.5)
part2*=temp
res = part1-part2
return res
Griewank’s Function
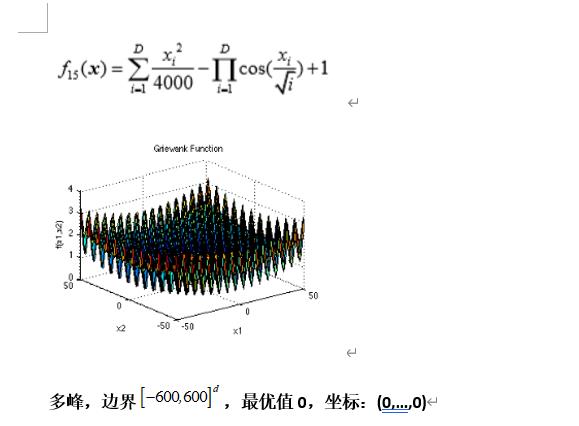
def F15(self,X):
part1 = 0.
part2 = 1
Dim = len(X)
for i in range(1,Dim+1):
part1+=X[i-1]*X[i-1]/4000
part2*=self.cos(X[i-1]/self.sqrt(i))
res = part1-part2 +1
return res
Katsuura Function
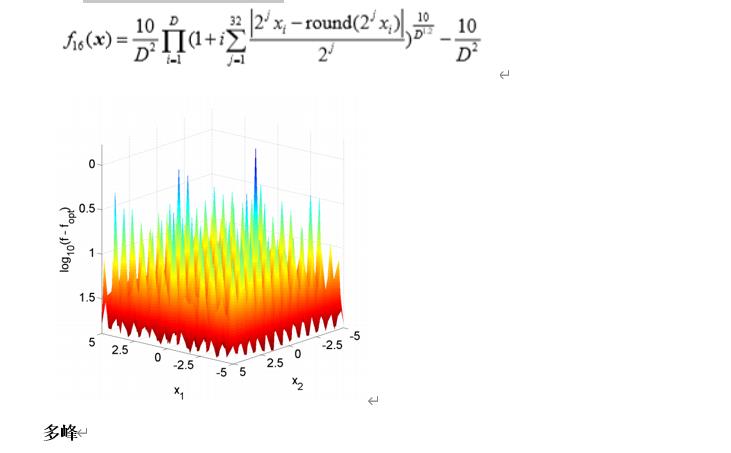
def F16(self,X):
Dim = len(X)
part1 = 1
for i in range(1,Dim+1):
temp=0.
for j in range(1,33):
temp+=abs(self.pow(2,j)*X[i-1]-round(self.pow(2,j)*X[i-1]))/2**j
temp = self.pow(1+i*temp,(10/Dim**1.2))
part1*=temp
res = (10/Dim**2)*part1-(10/Dim**2)
return res
HappyCat Function
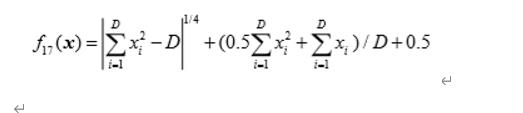
def F17(self,X):
Dim = len(X)
part1 = 0.
part2 = 0.
for x in X:
part1+=x*x
part2+=x
res = self.pow(abs(part1-Dim),0.25)+(0.5*part1+part2)/Dim + 0.5
return res
HGBat Function
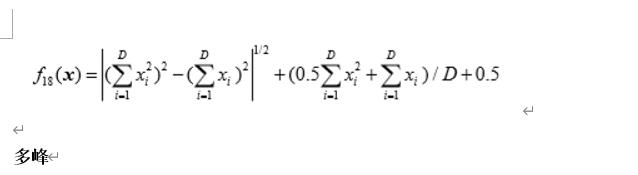
def F18(self,X):
Dim = len(X)
part1 = 0.
part2 = 0.
for x in X:
part1+=x*x
part2+=x
res = self.pow(abs(self.pow(part1,2)-self.pow(part2,2)),0.5)+(0.5*part1+part2)/Dim + 0.5
return res
Schaffer’s F7 Function
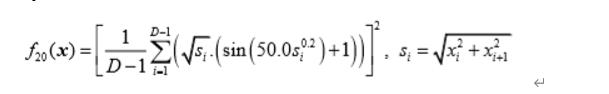
def F20(self,X):
Dim = len(X)
part1 = 0.
for i in range(0,Dim-1):
s = self.sqrt(X[i]**2+X[i+1]**2)
part1+=self.sqrt(s)*(self.sin(50.0*s**0.2)+1)
res = self.pow((1/(Dim-1))*part1,2)
return res
完整代码
import math
class Functions(object):
"""
先实例出对象来,减少new对象的时间,python优化
"""
pow = math.pow
cos = math.cos
sin = math.sin
pi = math.pi
exp = math.exp
sqrt = math.sqrt
e = math.e
def F1(self,X):
Dim = len(X)
res = X[0]*X[0]
temp = 0.
for i in range(2,Dim+1):
temp+=X[i-1]*X[i-1]
res+=self.pow(10,6)*temp
return res
def F2(self,X):
res = 0.
Dim = len(X)
for i in range(1,Dim+1):
res+=self.pow(abs(X[i-1]),(i+1))
return res
def F3(self,X):
part1 = 0.
part2 = 0.
for x in X:
part1+=x*x
part2+=0.5*x
res = part1+self.pow(part2,2)+self.pow(part2,4)
return res
def F4(self,X):
Dim = len(X)
res = 0.
for i in range(1,Dim):
res+=100*self.pow((self.pow(X[i-1],2)-X[i]),2)+(X[i-1]-1)+self.pow((X[i]-1),2)
return res
def F5(self,X):
res = 0.
for x in X:
res+=(x*x-10*self.cos(2*self.pi*x)+10)
return res
def __g(self,x1,x2):
res = 0.5+(self.pow(self.sin(self.sqrt(x1*x1+x2*x2)),2)/self.pow((1+0.001*(x1*x1+x2*x2)),2))
return res
def F6(self,X):
Dim = len(X)
res = 0.
for i in range(Dim-1):
res+=self.__g(X[i],X[i+1])
res+=self.__g(X[Dim-1],X[0])
return res
def __A(self, alpha,Dim,i):
res = self.pow(alpha,(i-1/Dim-1))
return res
def F8(self,X):
res = 0.
for x in X:以上是关于CEC2017基础函数说明Python版本的主要内容,如果未能解决你的问题,请参考以下文章