量化LDPC基于量化技术的LDPC译码算法的研究与matlab仿真

Posted 2022-07-12 fpga和matlab

1.本LDPC采用的量化方案

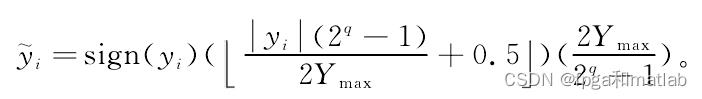
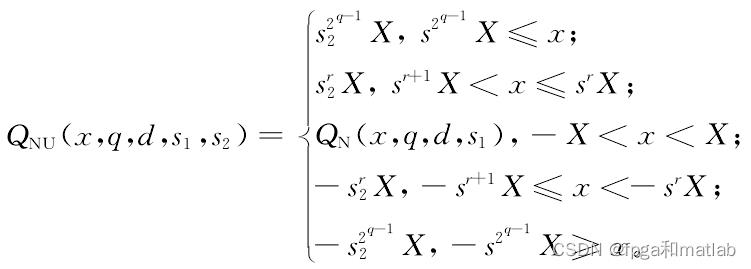
改进方案如下所示：

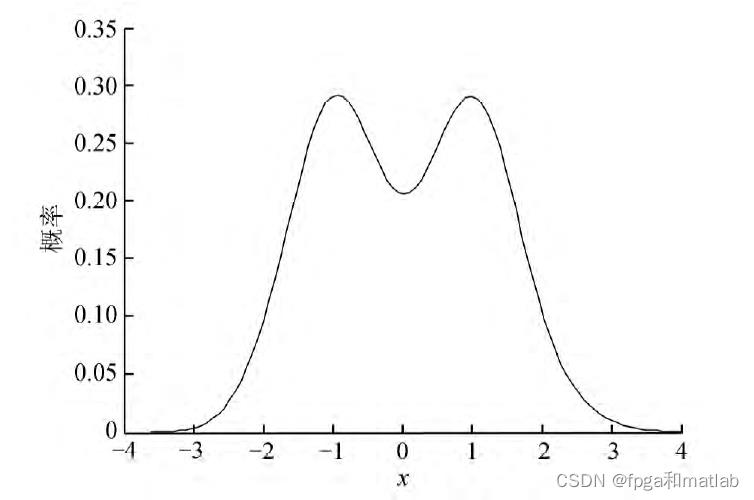    第一个量化公式，的范围是由一个统计范围得到的，但是在实际中，根据信道的不同，可能存在多种可能，这里，我们的考虑的方案是自适应的调整Ymax和Ymin，根据信道的大概估计结果对Ymax和Ymin进行调整，

 方案如下所示：

 

k1为0~1之间的值。在实际中，可以加入一个噪声估计模块，对难以确定的信道白噪声进行估计。

        这种改进方案的思路是，当噪声越大的时候，接收到信号的幅度波动范围也就越大，因此，其置信区间并不是一个固定的范围。对于第二个量化公式，采用的改进方案如下所示：

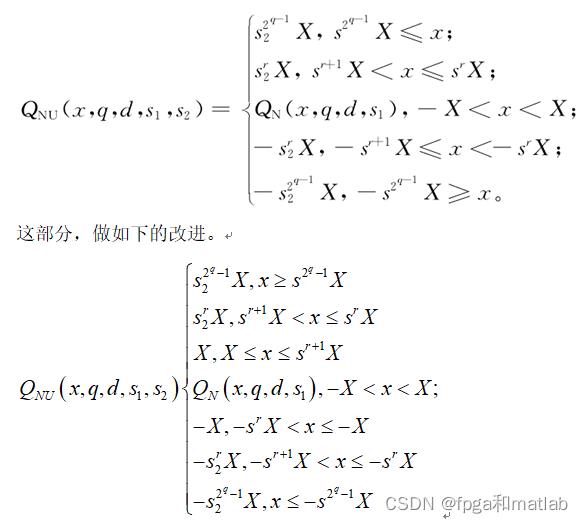
2.核心源码

function Q = func_QX(x);

q = 2;
s = 2;
s1= 1.7;
s2= 2;
d = 0.5;
N = 2^(q-1)-1;
r = 4;
Q = x;
tmp1=0;
for i = 1:N
    tmp1(i) = d*s1^(i-1);
end

X_= -sum(tmp1) + d/2;
X =  sum(tmp1) + d/2;


if x >= s^(2^q-1)*X
   Q =  s2^(2^q-1)*X;
end

if x > s^(r+1)*X & x <= s^(r)*X
   Q =  s2^(r)*X;
end

if x >= X & x <= s^(r+1)*X
   Q =  X;
end


if x > X_ & x < X
   Q =  QN(x,q,d,s1,N);
end

if x >= s^(r)*X_ & x < X_
   Q = X_;
end

if x >= s^(r+1)*X_ & x < s^(r)*X_
   Q =  s2^(r)*X_;
end

if x <= s^(2^q-1)*X_
   Q =  s2^(2^q-1)*X_;
end

end

function y = QN(x,q,d,s1,N);

tmp1=0;
for i = 1:N
    tmp1(i) = d*s1^(i-1);
end
tmp2=0;
for i = 1:N
    tmp2(i) = d*s1^(i-1);
end
A1 =  sum(tmp1) - d/2;
B1 =  sum(tmp2) - d/2;
A2 =  -sum(tmp1) + d/2;
B2 =  -sum(tmp2) + d/2;
y  = x;
if x >= A1 & x <= B1
   y =  sum(tmp2);
end    

if x >= -d/2 & x <= d/2
   y =  0;
end 


if x >= B2 & x <= A2
   y =  -sum(tmp2);
end  


end

clc;
clear;
close all;
warning off;
addpath 'func\\'
rng(1); 
%码率
Rate      = 13/24; %码率大于0.5，注意，码率不能任意设置的，这里可以设置为12/24~23/24
Lens      = 2400;%码长大于1000
%量化位宽
WB        = 6;%WB:1

%迭代次数
iter      = 5;

%基于IEEE802.16E的QC-LDPC构造
[Qc_H,Hb] = func_H(Lens,Rate);
k         = Rate*log2(2);
[RR,CC]   = size(Hb);
block     = Lens/CC;
SNRs      = [0.5:0.5:4];
 
Err       = [];
% [cycle6num,cycle8num] = func_loop_check(Qc_H);

for kj = 1:length(SNRs)
    kj
    SNR     = SNRs(kj)/k;
    sigma   = sqrt(1/(2*SNR));
    Ng      = 0.1;
    ofdm_N  = 256;                                        
    Lf      = 8;     
    Tx_dat  = round(rand(100000,1)); 
    %导频
    PN_train= [1 1 0 1 0 1 1 1 0 0];  
    Nfft    = 8*ofdm_N;  
    %cyclic prefix
    Np      = round(Ng*Nfft); 

    %LDPC
    Tx_dat_ldpc = [];
    for i = 1:floor(length(Tx_dat)/(Rate*Lens))+1
        i
        if i <= floor(length(Tx_dat)/(Rate*Lens))
           tmps = Tx_dat((i-1)*(Rate*Lens)+1:(i)*(Rate*Lens));
        else
           tmps = [Tx_dat((i-1)*(Rate*Lens)+1:end);zeros(Lens*Rate-length(Tx_dat((i-1)*(Rate*Lens)+1:end)),1)]; 
        end
         tmps_ldpc = func_ldpc_encode(tmps',Qc_H,Hb);
         Tx_dat_ldpc = [Tx_dat_ldpc,tmps_ldpc];
    end


    %QPSK                                       
    [mods,demods]    = func_MPSK(ofdm_N,'M',4,'SymbolOrder','Gray'); 
    %OFMD调制
    y_Tx_mod         = func_OFDM_mod(Tx_dat_ldpc,mods,Np,Lf,PN_train,Nfft);

    %发送，高斯白噪声
    y_Rx             = func_TRANSMITTER(y_Tx_mod,SNR);

    %OFMD解调
    [Rx_dat,Rx_dat2] = func_OFDM_demod(y_Rx,demods,Np,Lf,PN_train,Nfft);



    %LDPC译码
    Rx_dat_ldpc = [];
    for i = 1:floor(length(Rx_dat)/(Lens))
        i
        tmps        = Rx_dat((i-1)*(Lens)+1:(i)*(Lens));
        tmps_deldpc = func_ldpc_decodenew([2*tmps-1]',RR,CC,block,Qc_H,sigma,iter,WB);
        Rx_dat_ldpc = [Rx_dat_ldpc,abs(tmps_deldpc(1:Rate*Lens)-1)];
    end


    %计算误码率
    Rx_dat_ldpcs = Rx_dat_ldpc';
    bit_errors  = length(find(Tx_dat(1:length(Rx_dat_ldpcs)) ~=Rx_dat_ldpcs))/length(Tx_dat); 
    bit_errors
    Err     = [Err,bit_errors];
    clear bit_errors Rx_dat_ldpcs Rx_dat_ldpc tmps_deldpc tmps Rx_dat_ldpc Rx_dat Rx_dat2 y_Rx y_Tx_mod mods demods Tx_dat_ldpc tmps_ldpc Tx_dat_ldpc Tx_dat
end


figure;
semilogy(SNRs,Err,'b-o');
grid on
xlabel('SNR');
ylabel('Error');

save R.mat SNRs Err

3.仿真结果效果

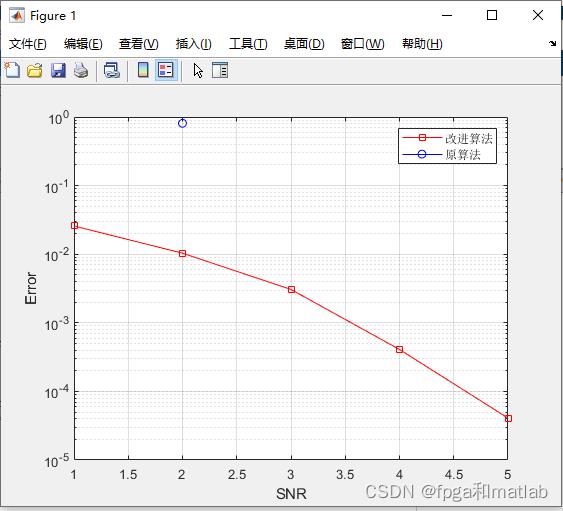
 A14-36