支持向量机

Posted 2022-07-01 一蓑烟雨晴

文章目录

• • 6.1 间隔与支持向量
  • 6.2 对偶问题
  • 6.3 核函数
  • 6.4 软间隔与正则化
  • 6.5 支持向量回归
  • 6.6 核方法
• 代码实现
• • 线性SVM
  • 多项式SVM
  • 高斯核SVM

6.1 间隔与支持向量

从几何角度，对线性可分数据集，支持向量机就是找距离正负样本都最远的超平面，相比于感知机，其解是唯一的，且不偏不倚，泛化性能更好。

给定训练样本集，分类学习最基本的想法就是基于训练集D在样本空间中找到一个划分超平面，将不同类别的样本分开，支持向量机倾向找到产生分类结果具有鲁棒性，对未见示例的泛化能力最强的划分超平面。

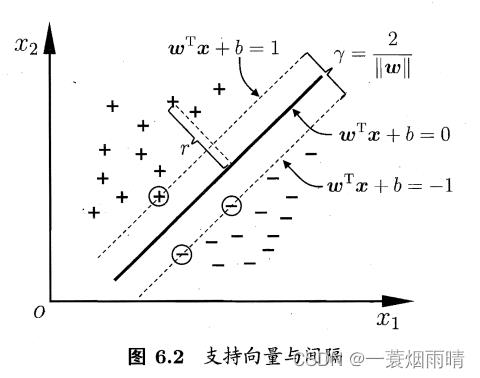
假设超平面能将训练样本正确分类，即
$$\begin{array}{ll}{\mathbf{w}}^{\mathrm{T}}{\mathbf{x}}_i+b⩾+1,& y_i=+1\\ {\mathbf{w}}^{\mathrm{T}}{\mathbf{x}}_i+b⩽-1,& y_i=-1\end{array}$$
距离超平面最近的几个训练样本点使得上式的等号成立，它们被称为“支持向量”，两个异类支持向量到超平面的距离之和为
$$\gamma =\frac{2}{\Vert \mathbf{w}\Vert }$$
它被称为“间隔”。
支持向量机是要找到具有“最大间隔”的划分超平面，即建立如下基本型：
$$\begin{array}{rl}\underset{\mathbf{w},b}{\min }& \frac{1}{2}\Vert \mathbf{w}{\Vert }^2\\ \text{ s.t. }& y_i\left({\mathbf{w}}^{\mathrm{T}}{\mathbf{x}}_i+b\right)⩾1,i=1,2,\dots ,m\end{array}$$
此处，有另一种解释得到上式

6.2 对偶问题

注意到本身上式是一个凸优化规划问题，能直接用现成的优化计算包求解，但是我们可以有更高效的方法。

下图来自B站白板推导

原问题等价于对偶问题的充要条件就是满足KKT条件

如何从下式求解${\alpha }_i$呢？
$$\underset{\mathbf{\alpha }}{\max }\sum _{i=1}^m{\alpha }_i-\frac{1}{2}\sum _{i=1}^m\sum _{j=1}^m{\alpha }_i{\alpha }_j{y}_i{y}_j{\mathbf{x}}_i^{\mathrm{T}}{\mathbf{x}}_j$$ $$\begin{array}{ll}\text{ s.t. }& {\sum }_{i=1}^m{\alpha }_i{y}_i=0\\ & {\alpha }_i⩾0,i=1,2,\dots ,m\end{array}$$
人们通过利用问题本身的特性，提出了很多高效算法，SMO是其中一个著名的代表。

6.3 核函数

在前面的讨论中，我们假设训练样本是线性可分的，然而现实中原始样本空间内也许并不存在一个能正确划分两类样本的超平面。
幸运的是，如果原始空间是有限维，即属性数有限，那么一定存在一个高维特征空间使样本可分。


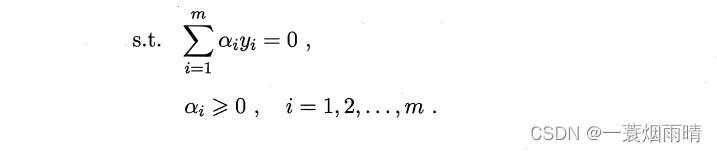
但是直接计算$\varphi {\left({\mathbf{x}}_i\right)}^{\mathrm{T}}\varphi \left({\mathbf{x}}_j\right)$通常是困难的，为了避开这个障碍，可以设想这样一个函数，即核函数：

$$\kappa \left({\mathbf{x}}_i,{\mathbf{x}}_j\right)=⟨\varphi \left({\mathbf{x}}_i\right),\varphi \left({\mathbf{x}}_j\right)⟩=\varphi {\left({\mathbf{x}}_i\right)}^{\mathrm{T}}\varphi \left({\mathbf{x}}_j\right)$$
以下是常用的几个核函数：

6.4 软间隔与正则化

现实任务中往往很难确定合适的核函数使得训练样本在特征空间中线性可分；退一步说，即便恰好找到了某个核函数使训练集在特征空间中线性可分，也很难断定这个貌似线性可分的结果不是由于过拟合所造成的。
缓解该问题的一个方法是允许支持向量机在一些样本上出错。

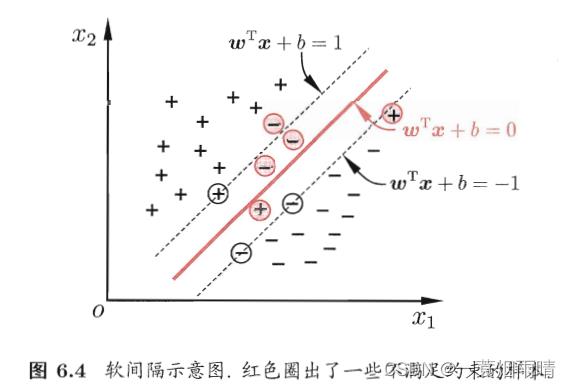
软间隔允许某些样本不满足约束，但在最大化间隔的同时，不满足约束的样本应尽可能少。于是有如下优化目标：
$$\underset{\mathbf{w},b}{\min }\frac{1}{2}\Vert \mathbf{w}{\Vert }^2+C\sum _{i=1}^m{\ell }_{0/1}(y_i(以上是关于支持向量机的主要内容，如果未能解决你的问题，请参考以下文章$$

西瓜书学习—支持向量机之最优化

求助半监督最小二乘支持向量机的MATLAB程序

优化分类基于matlab遗传算法优化支持向量机分类（多输入多分类）含Matlab源码 QF003期

反向支持向量机：计算预测

连续受限玻尔兹曼机

支持向量机SVM模型中C和gamma参数分别是什么？对模型有什么影响？