力扣leetcode算法-搜索插入位置

Posted 2022-06-24 、Dong

文章目录

• 一、题目描述
• 二、解题思路
• 结尾

---

一、题目描述

给定一个排序数组和一个目标值，在数组中找到目标值，并返回其索引。如果目标值不存在于数组中，返回它将会被按顺序插入的位置。 请必须使用时间复杂度为 O(log n) 的算法。

示例 1:
输入: nums = [1,3,5,6], target = 5 输出: 2

示例 2:
输入: nums = [1,3,5,6], target = 2 输出: 1

示例 3:
输入: nums = [1,3,5,6], target = 7 输出: 4
提示:
1 <= nums.length <= 10的4次幂
-10的4次幂 <= nums[i] <= 10的4次幂
nums 为无重复元素的升序排列数组
-10的4次幂<= target <= 10的4次幂

---

二、解题思路

思路及算法

假设题意是叫你在排序数组中寻找是否存在一个目标值，那么训练有素的读者肯定立马就能想到利用二分法在 O(logn) 的时间内找到是否存在目标值。但这题还多了个额外的条件，即如果不存在数组中的时候需要返回按顺序插入的位置，那我们还能用二分法么？答案是可以的，我们只需要稍作修改即可。

考虑这个插入的位置 pos，它成立的条件为：

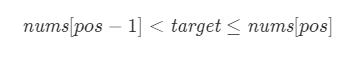
其中 nums 代表排序数组。由于如果存在这个目标值，我们返回的索引也是 pos，因此我们可以将两个条件合并得出最后的目标：「在一个有序数组中找第一个大于等于 target 的下标」。

问题转化到这里，直接套用二分法即可，即不断用二分法逼近查找第一个大于等于 target 的下标 。下文给出的代码是笔者习惯的二分写法，ans 初值设置为数组长度可以省略边界条件的判断，因为存在一种情况是 target 大于数组中的所有数，此时需要插入到数组长度的位置。

class Solution 
    public int searchInsert(int[] nums, int target) 
        int n = nums.length;
        int left = 0, right = n - 1, ans = n;
        while (left <= right) 
            int mid = ((right - left) >> 1) + left;
            if (target <= nums[mid]) 
                ans = mid;
                right = mid - 1;
             else 
                left = mid + 1;
            
        
        return ans;
    

复杂度分析

• 时间复杂度：O(logn)，其中 n 为数组的长度。二分查找所需的时间复杂度为 O(logn)。
• 空间复杂度：O(1)。我们只需要常数空间存放若干变量。

---

结尾

• 感谢大家的耐心阅读，如有建议请私信或评论留言。
• 如有收获，劳烦支持，关注、点赞、评论、收藏均可，博主会经常更新，与大家共同进步

CSDN 社区图书馆，开张营业！ 深读计划，写书评领图书福利~