从1到N整数中1出现的次数

Posted 2022-06-23 想名真难

给定一个整数 n，计算所有小于等于 n 的非负整数中数字 1 出现的个数。 
力扣

示例:

输入: 13
输出: 6 
解释: 数字 1 出现在以下数字中: 1, 10, 11, 12, 13 。

---

能想到最直观的方法(说实话 ,我没想到 , 第一眼我认为这是一个数学题, 根本没有想到用计算机的思路解决问题), 也就是累加1到n中每个整数1出现的次数。我们可以每次通过对10求余数判断整数的个位数字是不是1。如果这个数字大于10,除以10之后再判断个位数字是不是1。 所以第一个方法就出来了.  

这个算法还是很有必要的, 后续的算法需要依靠这个来验证是否正确 , 有了这个算法才能孵化出更好的算法.

class Solution 
    func countDigitOne(_ n: Int) -> Int 

        // 计算单个数字中包含的"1"个数
        func p_countOneNum(_ oneNum: Int) -> Int 
            var result = 0
            var tempNum = oneNum
            while tempNum > 0 
                if tempNum%10 == 1
                    result += 1
                
                tempNum /= 10
            
            return result
        

        var result = 0
        for i in 0...n 
            result += p_countOneNum(i)
        
        print("第一种算法:1-",n,"出现了",result,"个")
        return result
    

每一个数字都需要处理,需要N次; 
在对任意一个数字处理的时候 ,由于每次都是/10,  需要logN次 ;
总体的时间复杂度是O(N*logN). 

---

现在有了一个暂时能用的算法了, 现在把这个当成一个数学题 , 通过数学方法看看能不能求解. 

先来一个例子, 比如n=215.我们按照个位,十位,百位来计算每个位值上1出现的次数.

先从个位开始, 个位要想出现1,只有这种001,011,021,031,.......101,111,121,.....201,211 , 从001到211总共是22个, 其中21个是必定出现的, 最后一个211,需要看情况, 如果n=210,那么211就不会有了.

在看十位, 010,011,012,013,...,018,019,   110,111,112,113,....,118,119,   210,211,212,... 215, 总共是26个, 前面20个(2*10, 010到019, 110到119, )也是必定出现的, 后面的6个(210,211,212 ... 215)

在看百位,100,101,102,103...198,199,    总共出现了100个.

通过手动计算,发现总共是 22+26+100=148个.

在来一个例子, n=555,

个位上 , 总共出现了56次,  这个56次怎么出来的呢, 0-9完整的循环出现了55次,尾巴上0-5出现了1次,加起来是56次.

十位上,  总共出现了6次010-019, 110-119, 210-219,....510-519,     010到510完整出现了5次完整的,  每次有10个1 , 尾巴也是一个完整的, 因为十位的5比1大,所以总计是60个.

百位上, 出现了100次, 100-199, 尾巴的话是一个完整的, 因为百位的5比1大.

通过数学上的分析观看发现, 这个确实不好求,挺复杂的, 那咱们就一步一步来:

1出现的个数与  "所在的位数"  "有多少完整的数字循环" "这个位上的值是否大于1"  这些都有关,

• 这个位上的值是否大于1的影响, 这个影响到尾巴值 ,
  如果>1, 那就可以拿到这一位的所有值, 比如555,十位的5>1, 可以拿到一个完整十位上10个;  
  如果==0, 比如501中,十位为0, 则510,511,512...十位上是1个都拿不到 ;
  如果 == 1, 比如n=515, 十位为1, 可以拿到部分,510,511,512,513,...    余数+1, 
• 有多少完整的数字循环,  
  比如个位上有完整的 0~9, 就可以拿到 1个"1"
  十位上有完整的数字循环, 可以拿到 10~19, 共10个"1"
  百位上有完整的数字循环, 可以拿到100~199, 共100个"1"
• 在看位数的影响 , 如果是在百位 , 可以拿100个, 在10位最多是10个, 个位的话,最多1个. 位数影响了一个相乘系数.

总结来看 , 每一位似乎是一个  完整循环次数*系数 + 尾巴值  ,代码中我用的是 某位上1的个数 = times*X + tail,

times就是完整循环次数
X是系数, 和位数有关 , 个位只有1个,十位是10个,百位是100个.... ;
tail这个位数上的值与1的关系, 也就是尾巴值

按照这个理论计算一个进行验证,  以543为例 ,

• 个位出现543/10=54次完整的,X是1, 尾巴上是3 ,  3大于1 , 尾巴是1, 个位上总计55次
• 十位上, 543/100=5个完整的, X是10, 尾巴是4, 4大于1, 可以拿完整的10个, 十位上总计是60次
• 百位上, 543/1000=0个完整, X是100, 尾巴是5 , 5大于1, 可以拿完整的100个, 百位上是100次

信心满满, 开始操作.

func countDigitOne2(_ n: Int) -> Int 
    // 用来求个位/十位/百位上的数字
    var tempN = n
    var result = 0

    var X = 1
    while X <= n 
        // 计算 个位/十位/百位 完整出现了几次
        let times = n/(X*10)
        // each 保存个位/十位/百位 上"1"的个数, 某位上1的个数 = times*X + tail
        var each = times * X

        // 计算尾巴值, 默认尾巴可以拿到全部,下面分类讨论具体tail上的1
        var tail = X
        if tempN%10 == 1 
            tail = n%X + 1
         else if tempN%10 == 0 
            tail = 0
        

        each += tail
        print(n,"在",X,"位上出现了",each,"个")
        result += each

        tempN /= 10
        X *= 10
    
    print("第二种算法:1-",n,"出现了",result,"个")
    return result

 看起来效果不错, 至少543这个值是正确的, 测试用例来一波,  1~10000之间的数字逐个验证 ,  在随机1000个大数验证

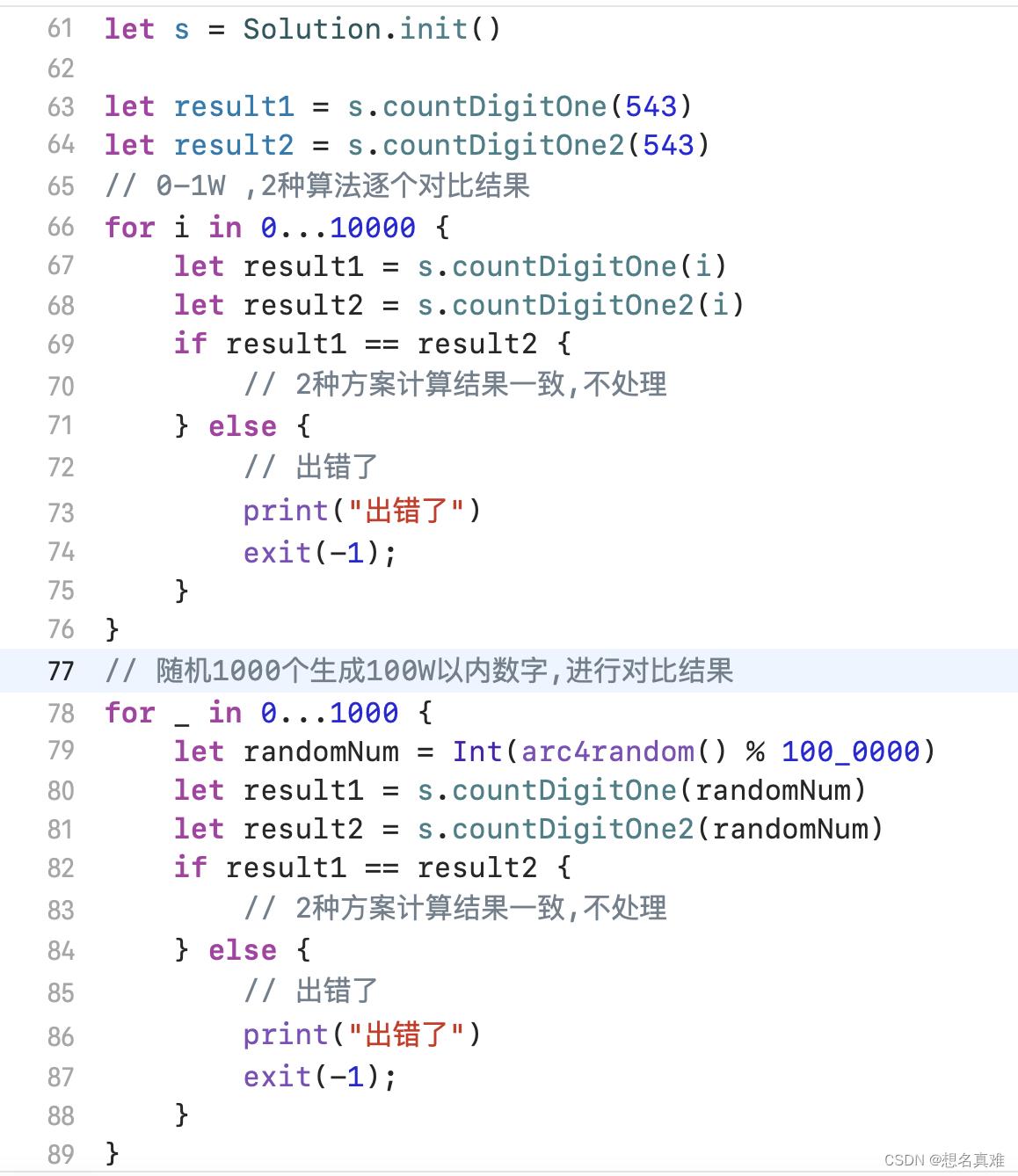
 时间上 第一个算法O(N*logN)明显慢了下来,  需要1-3秒了;  第二个算法O(logN)还是比较快的, 都是毫秒级的.

  最后LeetCode跑一下. 第一个算法超时, 第二个算法还不错.

---

 别看第二个算法 最后很简洁,  在实际写的过程中用了一晚上的时间才完善 , 总结出某位上1的个数 = times*X + tail, 找出这个关系之后才开始豁然开朗,一马平川起来.

最后提供一个c语言版本的.

int countDigitOne(int n)
    // 用来求个位/十位/百位上的数字
    int tempN = n;
    int  count = 0;
    // leetCodes上有个测试用例是一个很大的数字, 用long保证不会越界
    long b =1;
    while (b<=n) 
        
        // 个位/十位/百位 出现了几次
        int times = n/(b*10);
        // 出现次数*系数
        count += times * b;
        // 计算尾巴值, 默认可以拿到全部
        int tail = b;
        if (tempN%10 == 1) 
            tail = n%b+1;
         else if (tempN%10 == 0)
            tail = 0;
        
        count += tail;
        // NSLog(@"%d位上出现了%d个",b,count);
        
        tempN /= 10;
        b *= 10;
        
    
    
    // NSLog(@"第二种方法:1-%d之间出现了%d个",n,count);
    return count;