数字图像处理,基于PM和Catte模型各向异性扩散的C++实现
Posted EbowTang
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了数字图像处理,基于PM和Catte模型各向异性扩散的C++实现相关的知识,希望对你有一定的参考价值。
各向异性扩散原理及其概述
为了降低散斑噪声,1990年Perona和Malik提出了基于热扩散方程的各向异性扩散算法,由于该方法在去除噪声的同时能很好地保护边缘,因此该算法得到了广泛的应用。各向异性扩散属于偏微分方程方法,基于偏微分方程的去噪由于其对边缘及细节等的保护很好在去噪算法中得到了广泛的研究与应用。Perona-Malik扩散模型的提出引发了研究人员对各向异性扩散算法的研究热潮。1992年,Catte等人对PM模型进行了改进,提出了Catte模型,解决了PM模型中存在的问题,并在理论上证明了该模型满足解的适定性。之后又有许多学者提出PM模型的改进算法,这里不再提及。
1 经典的PM模型
针对各向同性扩散在去噪的同时会模糊图像的边缘,1990年,Perona和Malik在传统的热扩散方程的基础上,提出了基于非线性偏微分方程的新模型即各向异性扩散模型。
Perona和Malik提出的各项异性扩散模型如下:

式中:div是散度算子,∇为梯度算子,‖表示幅度,c(|∇I|)为扩散系数方程,I0为初始图像,t为引入的时间算子,表示降噪过程与扩散持续时间有关。Perona等给出了扩散系数函数的两种经典的选择:

其中,K为梯度阀值也就是扩散门限,∇I表示图像I的梯度,当∇I远大于梯度阀值K时,则c(|∇I|)趋于0,扩散过程被抑制;而∇I远小于梯度阀值K时,那么c(|∇I|)趋于1,则扩散过程被加强。
式(1)中的方程需要离散化之后,才能应用于图像去噪过程,其离散化形式如下:

PM模型还有一些缺点,第一,PM模型本身在数学上是一个病态的方程,不能保证解的存在性和唯一性;第二,PM模型对于孤立的噪声点及强噪声去噪效果不好,有时不仅不能消除噪声,反而会增强噪声。
2 Catte模型
为了解决PM模型的不足,Catte等人于1992年提出了改进的PM模型,本文称为Catte模型,该模型中首先使用高斯滤波对图像进行高斯平滑,采用平滑后的梯度模代替原始图像的梯度模,优化后的模型如下:

其中:Gσ是标准差为σ的高斯函数,“*“表示卷积。使用高斯平滑后的梯度模控制扩散的过程,克服了PM模型对噪声的敏感性,每次迭代先用高斯平滑对图像加以滤波,降低图像中强噪声的梯度,在消除噪声的同时又能保护边缘,这对于强噪声也能很好的去噪。Catte等人还证明了该模型是适定的,确保了扩散过程的稳定性。
虽然Catte模型获得了很好的去噪效果,但是模型中采用高斯平滑进行滤波,它不仅破坏了各向异性扩散的本质,而且会导致图像的结构偏离原始位置,边缘模糊性加大,此外,参数σ的选取也是该模型的一个难点,且σ趋于0时,模型变的不稳定。
3 PM模型的Matlab参考代码:
(参考于别人写的):function diff_im = anisodiff2D(im, num_iter, delta_t, kappa, option)
%ANISODIFF2D 经典PM模型的各向异性扩散
% DIFF_IM = ANISODIFF2D(IM, NUM_ITER, DELTA_T, KAPPA, OPTION)
% 该函数执行灰度图像上的各向异性扩散(经典PM模型),被认为是一个二维的网络结构的8个相邻节点的扩散传导。
%
% 参数描述:
% IM - 灰度图 (MxN).
% NUM_ITER - 迭代次数
% DELTA_T - 积分常数 (0 <= delta_t <= 1/7).通常情况下,由于数值稳定性,此参数设置为它的最大值。
% KAPPA - 控制传导的梯度模阈值。控制平滑。
% OPTION - 传导系数函数选择(Perona & Malik提出):
% 1 - c(x,y,t) = exp(-(nablaI/kappa).^2),
% privileges high-contrast edges over low-contrast ones.
% 2 - c(x,y,t) = 1./(1 + (nablaI/kappa).^2),
% privileges wide regions over smaller ones.
%
% 输出描述:
% DIFF_IM - 具有最大尺度空间参数的(扩散)图像。
%
% 使用例子:
% -------------
% s = phantom(512) + randn(512);
% num_iter = 15;
% delta_t = 1/7;%越大越平滑
% kappa = 30;%越大越平滑
% option = 2;
% ad = anisodiff2D(s,num_iter,delta_t,kappa,option);
% figure, subplot 121, imshow(s,[]), subplot 122, imshow(ad,[]);
% 转换输入图像类型为double.
im = double(im);
% PDE(偏微分方程)的初始条件。
diff_im = im;
% 中心像素距离。
dx = 1;
dy = 1;
dd = sqrt(2);
% 二维卷积掩模-8个方向上的梯度差分。
hN = [0 1 0; 0 -1 0; 0 0 0];
hS = [0 0 0; 0 -1 0; 0 1 0];
hE = [0 0 0; 0 -1 1; 0 0 0];
hW = [0 0 0; 1 -1 0; 0 0 0];
hNE = [0 0 1; 0 -1 0; 0 0 0];
hSE = [0 0 0; 0 -1 0; 0 0 1];
hSW = [0 0 0; 0 -1 0; 1 0 0];
hNW = [1 0 0; 0 -1 0; 0 0 0];
% 各向异性扩散
for t = 1:num_iter
% 8个方向梯度差分. [imfilter(.,.,'conv') 也可以使用 conv2(.,.,'same')]
nablaN = imfilter(diff_im,hN,'conv');
nablaS = imfilter(diff_im,hS,'conv');
nablaW = imfilter(diff_im,hW,'conv');
nablaE = imfilter(diff_im,hE,'conv');
nablaNE = imfilter(diff_im,hNE,'conv');
nablaSE = imfilter(diff_im,hSE,'conv');
nablaSW = imfilter(diff_im,hSW,'conv');
nablaNW = imfilter(diff_im,hNW,'conv');
% 扩散函数
if option == 1
cN = exp(-(nablaN/kappa).^2);
cS = exp(-(nablaS/kappa).^2);
cW = exp(-(nablaW/kappa).^2);
cE = exp(-(nablaE/kappa).^2);
cNE = exp(-(nablaNE/kappa).^2);
cSE = exp(-(nablaSE/kappa).^2);
cSW = exp(-(nablaSW/kappa).^2);
cNW = exp(-(nablaNW/kappa).^2);
elseif option == 2
cN = 1./(1 + (nablaN/kappa).^2);
cS = 1./(1 + (nablaS/kappa).^2);
cW = 1./(1 + (nablaW/kappa).^2);
cE = 1./(1 + (nablaE/kappa).^2);
cNE = 1./(1 + (nablaNE/kappa).^2);
cSE = 1./(1 + (nablaSE/kappa).^2);
cSW = 1./(1 + (nablaSW/kappa).^2);
cNW = 1./(1 + (nablaNW/kappa).^2);
end
% 离散偏微分方程的解决方案
diff_im = diff_im + ...
delta_t*(...
(1/(dy^2))*cN.*nablaN + (1/(dy^2))*cS.*nablaS + ...
(1/(dx^2))*cW.*nablaW + (1/(dx^2))*cE.*nablaE + ...
(1/(dd^2))*cNE.*nablaNE + (1/(dd^2))*cSE.*nablaSE + ...
(1/(dd^2))*cSW.*nablaSW + (1/(dd^2))*cNW.*nablaNW );
% 迭代的警告
fprintf('\\rIteration %d\\n',t);
end4 PM模型的C++参考代码:
完全改写于上,与上面的计算结果一模一样!void Perona_Malik(
unsigned char* inbuffer,
int iter,
double delta_t,
double kappa,
int option,
int width,
int height,
unsigned char* outbuffer
)
double dx = 1.0;
double dy = 1.0;
double dd = sqrt(2.0);
//变换数据类型,准备处理
double* tmpbuffer1 = new double[width*height];
double* tmpbuffer2 = new double[width*height];
for (int kk = 0; kk < width*height; kk++)
tmpbuffer1[kk] = double(inbuffer[kk]);
tmpbuffer2[kk] = double(inbuffer[kk]);
int i, j;
double cN = 0.0, cS = 0.0, cE = 0.0, cW = 0.0;
double cNE = 0.0, cSE = 0.0, cSW = 0.0, cNW = 0.0;
double nablaN = 0.0, nablaS = 0.0, nablaE = 0.0, nablaW = 0.0;
double nablaNE = 0.0, nablaSE = 0.0, nablaNW = 0.0, nablaSW = 0.0;
for (int t = 0; t < iter; t++)//迭代次数
for (i = 0; i < height; i++)
for (j = 0; j < width; j++)//列
double pixel = -tmpbuffer1[i*height + j];
nablaS = nablaE = nablaW = nablaN = pixel;
nablaNE = nablaSE = nablaNW = nablaSW = pixel;
//八个方向上的求导
if (i + 1 < height)//不是最后一行
nablaN += tmpbuffer1[(i + 1)*height + j];
if (i > 0)//不是第一行
nablaS += tmpbuffer1[(i - 1)*height + j];
if (j + 1 < width)//不是最后一列
nablaE += tmpbuffer1[i*height + j + 1];
if (j > 0)//不是第一列
nablaW += tmpbuffer1[i*height + j - 1];
if (i + 1 < height && j > 0)
nablaNE += tmpbuffer1[(i + 1)*height + j -1 ];
if (i > 0 && j > 0)
nablaSE += tmpbuffer1[(i - 1)*height + j - 1];
if (i > 0 && j + 1 < width)
nablaNW += tmpbuffer1[(i - 1)*height + j + 1];
if (i + 1 < height && j + 1 < width)
nablaSW += tmpbuffer1[(i + 1)*height + j + 1];
cN = 0.0, cS = 0.0, cE = 0.0, cW = 0.0;
if (1 == option)//扩散函数的选择
cN = exp(-(nablaN / kappa) * (nablaN / kappa));
cS = exp(-(nablaS / kappa) * (nablaS / kappa));
cE = exp(-(nablaE / kappa) * (nablaE / kappa));
cW = exp(-(nablaW / kappa) * (nablaW / kappa));
cNE = exp(-(nablaNE / kappa) * (nablaNE / kappa));
cSE = exp(-(nablaSE / kappa) * (nablaSE / kappa));
cSW = exp(-(nablaSW / kappa) * (nablaSW / kappa));
cNW = exp(-(nablaNW / kappa) * (nablaNW / kappa));
else if (2 == option)
cN = 1.0 / (1 + (nablaN / kappa) * (nablaN / kappa));
cS = 1.0 / (1 + (nablaS / kappa) * (nablaS / kappa));
cE = 1.0 / (1 + (nablaE / kappa) * (nablaE / kappa));
cW = 1.0 / (1 + (nablaW / kappa) * (nablaW / kappa));
cNE = 1.0 / (1 + (nablaNE / kappa) * (nablaNE / kappa));
cSE = 1.0 / (1 + (nablaSE / kappa) * (nablaSE / kappa));
cSW = 1.0 / (1 + (nablaSW / kappa) * (nablaSW / kappa));
cNW = 1.0 / (1 + (nablaNW / kappa) * (nablaNW / kappa));
tmpbuffer2[i*height + j] += delta_t * ( 1.0 / (dy*dy)*cN * nablaN + 1.0 / (dy*dy)*cS * nablaS +1.0 / (dx*dx)*cE * nablaE + 1.0 / (dx*dx)*cW * nablaW +
1.0 / (dd *dd)*cNE*nablaNE + 1.0 / (dd *dd)*cSE*nablaSE +1.0 / (dd *dd)*cSW*nablaSW + 1.0 / (dd*dd)*cNW*nablaNW);
for (int kk = 0; kk < width*height; kk++)
tmpbuffer1[kk] = tmpbuffer2[kk];
// 迭代结束
// 转换成图像数据
for (int kk = 0; kk < height*width; kk++)
outbuffer[kk] = unsigned char(max(0, min(tmpbuffer2[kk], 255)));
delete[] tmpbuffer2;
tmpbuffer2 = NULL;
delete[] tmpbuffer1;
tmpbuffer1 = NULL;
PM模型实验测试:
PM模型图像去噪测试实验:
以下所有结果均为C++处理。 1,对原图像进行处理的结果 参数为: int iter = 30;double delta_t = 1.0 / 7.0;
double kappa = 10.0;
int option = 2;
可以发现对边缘有就较好的保护能力:(左为原图)


2,对噪声图像进行处理的结果
注意这是matlab里面的乘性噪声,去噪效果一般!


PM模型对比小波阈值算法的一维信号去噪测试实验:
clc;
clear;
% 获取噪声信号
load leleccum;
indx = 2500:3450;
noisez = leleccum(indx);
%%%%%%%%%%%%%%%%%%%%%%%一维小波阈值去噪%%%%%%%%%%%%%%%%%%%%%%%%
%信号的分解
wname = 'db3';
lev = 3;
[c,l] = wavedec(noisez,lev,wname);
%求取阈值
sigma = wnoisest(c,l,1);%使用库函数wnoisest提取第一层的细节系数来估算噪声的标准偏差
N = numel(noisez);%整个信号的长度
thr = sigma*sqrt(2*log(N));%最终阈值
%全局阈值处理
keepapp = 1;%近似系数不作处理
denoisexs = wdencmp('gbl',c,l,wname,lev,thr,'s',keepapp);
denoisexh = wdencmp('gbl',c,l,wname,lev,thr,'h',keepapp);
%%%%%%%%%%%%%%%%%%%%%%%一维各异性扩撒%%%%%%%%%%%%%%%%%%%%%%%%%%%%
num_iter = 15;
delta_t = 1/3;
kappa = 30;
option = 2;
denoisead = anisodiff1D(noisez,num_iter,delta_t,kappa,option);
% 作图
subplot(411),
plot(noisez), title('原始噪声信号');
subplot(412),
plot(denoisexs), title('小波软阈值去噪信号') ;
subplot(413),
plot(denoisexh), title('小波硬阈值去噪信号') ;
subplot(414),
plot(denoisead), title('各异性扩撒去噪信号') ; 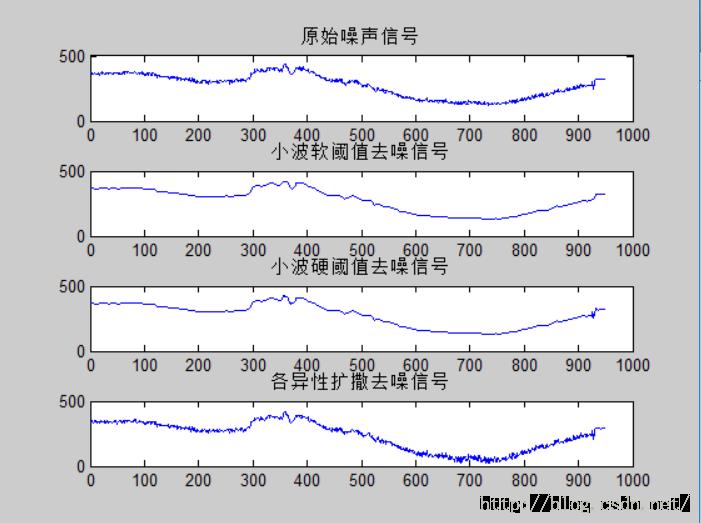
另一种一维信号的测试效果: 该一维信号为: noisez = exp(-(-10:0.1:10).^2/2.5)' + rand(length(-10:0.1:10),1);
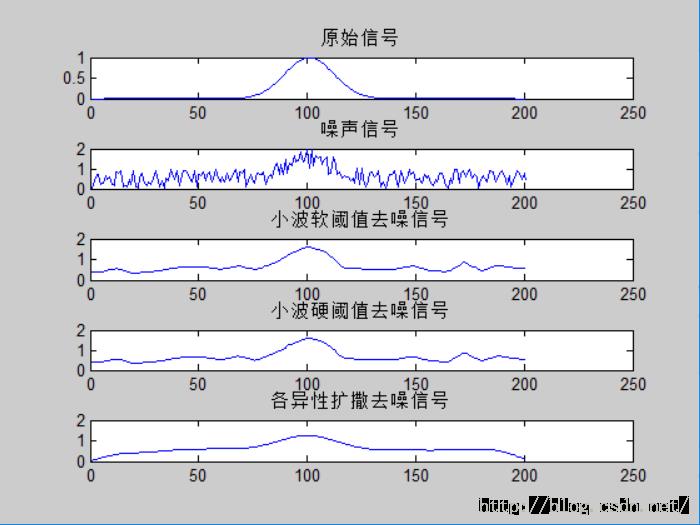
还是小波阈值去噪好!
其中一维个异性扩散代码如下:
function diff_sig = anisodiff1D(sig, num_iter, delta_t, kappa, option)
%ANISODIFF1D Conventional anisotropic diffusion
% DIFF_SIG = ANISODIFF1D(SIG, NUM_ITER, DELTA_T, KAPPA, OPTION) perfoms
% conventional anisotropic diffusion (Perona & Malik) upon 1D signals.
% A 1D network structure of 2 neighboring nodes is considered for diffusion
% conduction.
%
% ARGUMENT DESCRIPTION:
% SIG - input column vector (Nx1).
% NUM_ITER - number of iterations.
% DELTA_T - integration constant (0 <= delta_t <= 1/3).
% Usually, due to numerical stability this
% parameter is set to its maximum value.
% KAPPA - gradient modulus threshold that controls the conduction.
% OPTION - conduction coefficient functions proposed by Perona & Malik:
% 1 - c(x,t) = exp(-(nablaI/kappa).^2),
% privileges high-contrast edges over low-contrast ones.
% 2 - c(x,t) = 1./(1 + (nablaI/kappa).^2),
% privileges wide regions over smaller ones.
%
% OUTPUT DESCRIPTION:
% DIFF_SIG - (diffused) signal with the largest scale-space parameter.
%
% Example
% -------------
% s = exp(-(-10:0.1:10).^2/2.5)' + rand(length(-10:0.1:10),1);
% num_iter = 15;
% delta_t = 1/3;
% kappa = 30;
% option = 2;
% ad = anisodiff1D(s,num_iter,delta_t,kappa,option);
% figure, subplot 121, plot(s), axis([0 200 0 2]), subplot 122, plot(ad), axis([0 200 0 2])
%
% See also anisodiff2D, anisodiff3D.
% References:
% P. Perona and J. Malik.
% Scale-Space and Edge Detection Using Anisotropic Diffusion.
% IEEE Transactions on Pattern Analysis and Machine Intelligence,
% 12(7):629-639, July 1990.
%
% G. Grieg, O. Kubler, R. Kikinis, and F. A. Jolesz.
% Nonlinear Anisotropic Filtering of MRI Data.
% IEEE Transactions on Medical Imaging,
% 11(2):221-232, June 1992.
%
% MATLAB implementation based on Peter Kovesi's anisodiff(.):
% P. D. Kovesi. MATLAB and Octave Functions for Computer Vision and Image Processing.
% School of Computer Science & Software Engineering,
% The University of Western Australia. Available from:
% <http://www.csse.uwa.edu.au/~pk/research/matlabfns/>.
%
% Credits:
% Daniel Simoes Lopes
% ICIST
% Instituto Superior Tecnico - Universidade Tecnica de Lisboa
% danlopes (at) civil ist utl pt
% http://www.civil.ist.utl.pt/~danlopes
%
% May 2007 original version.
% Convert input signal to double.
sig = double(sig);
% PDE (partial differential equation) initial condition.
diff_sig = sig;
% Center point distance.
dx = 1;
% 1D convolution masks - finite differences.
hW = [1 -1 0]';
hE = [0 -1 1]';
% Anisotropic diffusion.
for t = 1:num_iter
% Finite differences. [imfilter(.,.,'conv') can be replaced by conv(.,.,'same')]
nablaW = imfilter(diff_sig,hW,'conv');
nablaE = imfilter(diff_sig,hE,'conv');
% Diffusion function.
if option == 1
cW = exp(-(nablaW/kappa).^2);
cE = exp(-(nablaE/kappa).^2);
elseif option == 2
cW = 1./(1 + (nablaW/kappa).^2);
cE = 1./(1 + (nablaE/kappa).^2);
end
% Discrete PDE solution.
diff_sig = diff_sig + ...
delta_t*(...
(1/(dx^2))*cW.*nablaW + (1/(dx^2))*cE.*nablaE);
% Iteration warning.
fprintf('\\rIteration %d\\n',t);
end记录一份别人写的代码:
(PM和Catte模型均有)clear all;
close all;
clc;
Image = imread('Barbara.bmp'); %输入图像
Image = double(Image); %图像类型uint8转换为double
figure(1); imshow(uint8(Image));title('原始图像'); %显示图像
Image_noise = Image + 10*randn(size(Image)); %添加高斯白噪声
figure(2); imshow(uint8(Image_noise)); title('加高斯白噪声'); %显示噪声图像
%%%%%%%%%%%%%%%%%%%%%%%%%%%% P_M %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
PM_num=10; %循环次数
PM_threshold=50; %梯度阈值
lambda=0.1; %时间步长
PMchoice=1; %选择方程形式
PMImg = Image_noise; %初始化
[pmrows,pmcols] = size(PMImg);
for i = 1:PM_num
PMImg1 = zeros(pmrows+2, pmcols+2);
PMImg1(2:pmrows+1, 2:pmcols+1) = PMImg;
%向前差分计算4个方向的梯度
deltaN = PMImg1(1:pmrows,2:pmcols+1) - PMImg;
deltaS = PMImg1(3:pmrows+2,2:pmcols+1) - PMImg;
deltaE = PMImg1(2:pmrows+1,3:pmcols+2) - PMImg;
deltaW = PMImg1(2:pmrows+1,1:pmcols) - PMImg;
if PMchoice == 1
cN = exp(-(deltaN/PM_threshold).^2);
cS = exp(-(deltaS/PM_threshold).^2);
cE = exp(-(deltaE/PM_threshold).^2);
cW = exp(-(deltaW/PM_threshold).^2);
elseif PMchoice == 2
cN = 1./(1 + (deltaN/PM_threshold).^2);
cS = 1./(1 + (deltaS/PM_threshold).^2);
cE = 1./(1 + (deltaE/PM_threshold).^2);
cW = 1./(1 + (deltaW/PM_threshold).^2);
end
PMImg = PMImg + lambda*(cN.*deltaN + cS.*deltaS + cE.*deltaE + cW.*deltaW);
end
figure(3);imshow(uint8(PMImg));title('P-M');%显示PM模型处理的图像
%%%%%%%%%%%%%%%%%%%%%%%%%% Catte %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
num=8; %循环次数
threshold=50; %梯度阈值
la=0.1; %时间步长
choice=1; %选择方程形式
sgma=0.5;
GaussKernel=fspecial('Gaussian',3,sgma); % 高斯核
CImg = Image_noise; %初始化
[rows,cols] = size(CImg);
for i = 1:num
CImg_back=CImg;
CImg_back=conv2(CImg_back,GaussKernel,'same');
[CImgx,CImgy] = gradient(CImg_back); %计算梯度
gradCImg = sqrt(CImgx.^2+CImgy.^2); %计算梯度模值
%计算边缘函数g
if choice == 1
g = exp(-(gradCImg/threshold).^2);
elseif choice == 2
g = 1./(1+(gradCImg/threshold).^2);
end
CImg_x_e = CImg(:,[2:cols,cols])-CImg;
g_e = 0.5*(g(:,[2:cols,cols])+g);
Term_e = g_e.*CImg_x_e;
CImg_x_w = CImg - CImg(:,[1 1:cols-1]);
g_w = 0.5*(g(:,[1 1:cols-1])+g);
Term_w = g_w.*CImg_x_w;
CImg_y_s = CImg([2:rows,rows],:)-CImg;
g_s = 0.5*(g([2:rows,rows],:)+g);
Term_s = g_s.*CImg_y_s;
CImg_y_n = CImg-CImg([1 1:rows-1],:);
g_n = 0.5*(g([1,1:rows-1],:)+g);
Term_n = g_n.*CImg_y_n;
divgn = Term_e - Term_w + Term_s - Term_n;
CImg = CImg + la*divgn;
end
figure(4);imshow(uint8(CImg));title('Catte')%显示Catte模型处理的图像参考文献:
【1】P. Perona and J. Malik. Scale-Space and Edge Detection Using Anisotropic Diffusion.IEEE Transactions on Pattern Analysis and Machine Intelligence, 12(7):629-639, July 1990.
【2】一点一滴完全突破KAZE特征检测算法,从各向异性扩散滤波开始(1)
【3】CSDN网友,http://blog.csdn.net/cyh706510441/article/details/45248049
【4】毕业论文《MATLAB_偏微分方程图像平滑》
以上是关于数字图像处理,基于PM和Catte模型各向异性扩散的C++实现的主要内容,如果未能解决你的问题,请参考以下文章