Coursera TensorFlow 基础课程-week3

Posted 2022-06-21 fansy1990

Enhancing Vision with Convolutional Neural Networks

参考：Ubuntu 16 安装TensorFlow及Jupyter notebook 安装TensorFlow。

本篇博客翻译来自 Introduction to TensorFlow for Artificial Intelligence, Machine Learning, and Deep Learning

仅供学习、交流等非盈利性质使用！！！

其他相关文章
Coursera TensorFlow 基础课程-week4
Coursera TensorFlow 基础课程-week3
Coursera TensorFlow 基础课程-week2
Coursera TensorFlow 基础课程-week1

文章目录

• Enhancing Vision with Convolutional Neural Networks
• • 1. convolutions and pooling （卷积和池化）
  • 2.实现卷积和池化
  • 3. 使用卷积优化Fashion Mnist数据识别模型
  • 4. 可视化卷积结果
  • 5. 纯Python理解卷积和池化
  • 6. 测验：
  • 7. 额外练习：

1. convolutions and pooling （卷积和池化）

在进行图像处理的过程中，经常会使用滤波器矩阵（Filter）来对原始图片进行处理，而这个过程就是卷积（convolutions）。
如下图所示：

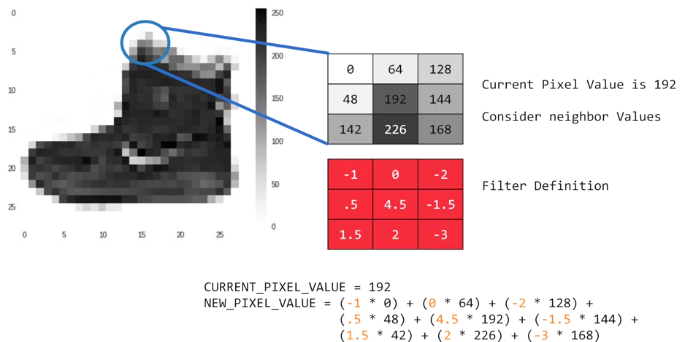
在上图中，针对其中的一个像素点，应用滤波器矩阵（图中给出的矩阵是随机定义的一个矩阵），那么卷积就是针对每个像素点，考虑其上下左右、左上下、右上下的邻居像素点，和滤波器矩阵对应点相乘得到新的像素点，这个转换过程就叫做卷积。

应用卷积可以具有特殊意义，如下两个图：

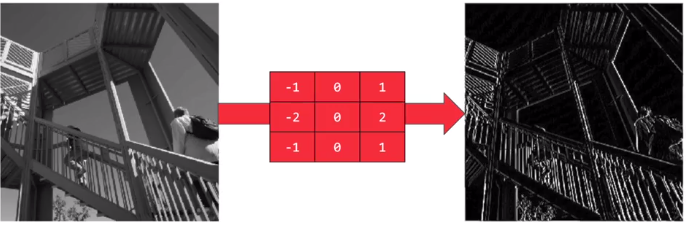
应用滤波器，可以把纵向特征明显化（即垂直特征明显）；

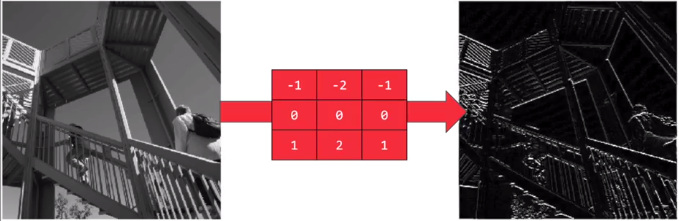
而应用这个滤波器，则可以把横向特征明显化（即水平特征明显）；

关于图像的卷积意义，推荐这篇博客： 理解图像卷积操作的意义

池化：简单理解，就是图片的压缩，即把原始比如128*128像素的图片压缩成28*28的图片。

一个简单的例子，如下图：

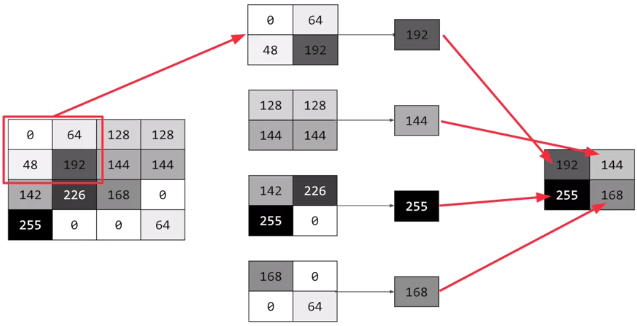
在图中，一个4*4像素的图片，被压缩为2*2的图片。其做法是：每次处理4个像素，找到其最大的像素进行返回。当然这只是其中的一种池化方法，你也可以针对4个像素进行求均值然后返回也可以。

2.实现卷积和池化

之前的代码：

model = tf.keras.models.Sequential([ 
    tf.keras.layers.Flatten(), 
    tf.keras.layers.Dense(128, activation=tf.nn.relu),
    tf.keras.layers.Dense(10, activation=tf.nn.softmax)])

在这个代码基础上，如何修改，可以添加卷积和池化层呢？
如下代码所示：

model = tf.keras.models.Sequential([
	tf.keras.layers.Conv2D(64,(3,3), activation='relu',input_shape=(28,28,1)),
	tf.keras.layers.MaxPooling2D(2,2),
	tf.keras.layers.Conv2D(64,(3,3),activation='relu'),
	tf.keras.layers.MaxPooling2D(2,2),
	tf.keras.layers.Flatten(), 
    tf.keras.layers.Dense(128, activation=tf.nn.relu), 
    tf.keras.layers.Dense(10, activation=tf.nn.softmax)
])

从代码中可看成：

1. 最后三行是和之前一样的；
2. 第二行，定义了一个卷积层（Conv2D)，这个卷积层有64个滤波器矩阵，每个矩阵是一个3*3的矩阵，activation是relu（会丢弃负值），而input_shape中的值是（28,28,1）,前面的28,28是图片的大小，而最后一个代表的是像素点的值，即图片是灰度图；
3. 第二行的卷积层中的64个滤波器矩阵里面的值，最开始是随机的，随着训练的推进，这些值会被改变，而改变的方向则是使得最终预测效果较好的方向。
4. 第三行是一个池化层，MaxPooling意味着最大值保留，同时池化的大小是(2,2),那么一次会处理4个像素点；
5. 第四、五行继续添加了一个卷积层和池化层；
6. 当一个图片经过2个卷积、池化层后，即叨叨Flatten时，图片会被缩小；
7. 缩小的图片，其实指的是对于目标变量更有话语权的特征被筛选出来；

通过下面的代码可以查看构造的模型：

model.summary()

那么，上面构造的模型的summary是什么呢？如下所示：

_________________________________________________________________
Layer (type)                 Output Shape              Param #   
=================================================================
conv2d (Conv2D)              (None, 26, 26, 64)        640       
_________________________________________________________________
max_pooling2d (MaxPooling2D) (None, 13, 13, 64)        0         
_________________________________________________________________
conv2d_1 (Conv2D)            (None, 11, 11, 64)        36928     
_________________________________________________________________
max_pooling2d_1 (MaxPooling2 (None, 5, 5, 64)          0         
_________________________________________________________________
flatten (Flatten)            (None, 1600)              0         
_________________________________________________________________
dense (Dense)                (None, 128)               204928    
_________________________________________________________________
dense_1 (Dense)              (None, 10)                1290      
=================================================================
Total params: 243,786
Trainable params: 243,786
Non-trainable params: 0

从上面的数据结果可以看出:

1. 第一层卷积输出的大小是26*26*64 ,这是什么意思呢？

首先，一个28*28的图片数据经过卷积层的滤波器矩阵后，其图片变为26*26的大小。由于滤波器大小是3*3，所以原始28*28的图像的最外面的一圈像素点是不能被计算的。这样上下左右就会各少一个像素点，所以得到的是26*26的图片。

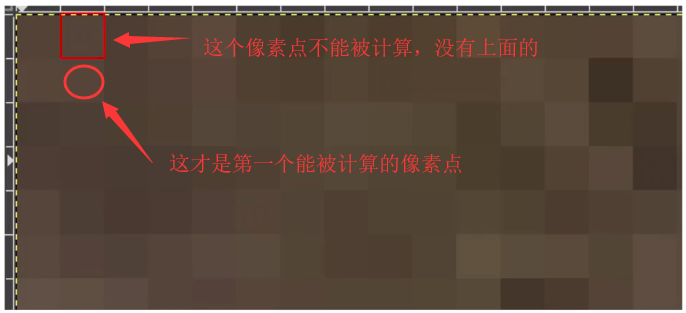
所以，如果滤波器是5*5，那么输出是多少呢？ （应该是24*24，会少4个像素点）。

其次，64代表64个滤波器，那么一个图片就会输出64个新的图片。

2. 第一个池化层，由于其大小是2*2，所以会把4个像素点变成一个，所以26*26的像素点，会变成13*13。
3. 第二个卷积层是类似的，像素会减小2，所以是11*11.
4. 第二个池化层，会把输入像素减半，即变成5*5 。
5. Flatten层的输入为什么是1600？ 1600 = 5*5*64，即把64个子图的所有像素点展平，作为Flatten的输入。

3. 使用卷积优化Fashion Mnist数据识别模型

之前的训练代码：

import tensorflow as tf
mnist = tf.keras.datasets.fashion_mnist
(training_images, training_labels), (test_images, test_labels) = mnist.load_data()
training_images=training_images / 255.0
test_images=test_images / 255.0
model = tf.keras.models.Sequential([
  tf.keras.layers.Flatten(),
  tf.keras.layers.Dense(128, activation=tf.nn.relu),
  tf.keras.layers.Dense(10, activation=tf.nn.softmax)
])
model.compile(optimizer='adam', loss='sparse_categorical_crossentropy', metrics=['accuracy'])
model.fit(training_images, training_labels, epochs=5)

test_loss = model.evaluate(test_images, test_labels)

执行完成后，可以得到训练集和测试集的误差及正确率，如下：

Epoch 1/5
60000/60000 [==============================] - 20s 340us/sample - loss: 0.4971 - acc: 0.8251
Epoch 2/5
60000/60000 [==============================] - 18s 306us/sample - loss: 0.3769 - acc: 0.8643
Epoch 3/5
60000/60000 [==============================] - 18s 292us/sample - loss: 0.3389 - acc: 0.8759
Epoch 4/5
60000/60000 [==============================] - 17s 291us/sample - loss: 0.3154 - acc: 0.8850
Epoch 5/5
60000/60000 [==============================] - 14s 230us/sample - loss: 0.2971 - acc: 0.8921
10000/10000 [==============================] - 2s 151us/sample - loss: 0.3676 - acc: 0.8657

改进后的代码，如下：

import tensorflow as tf
print(tf.__version__)
mnist = tf.keras.datasets.fashion_mnist
(training_images, training_labels), (test_images, test_labels) = mnist.load_data()
training_images=training_images.reshape(60000, 28, 28, 1)
training_images=training_images / 255.0
test_images = test_images.reshape(10000, 28, 28, 1)
test_images=test_images/255.0
model = tf.keras.models.Sequential([
  tf.keras.layers.Conv2D(64, (3,3), activation='relu', input_shape=(28, 28, 1)),
  tf.keras.layers.MaxPooling2D(2, 2),
  tf.keras.layers.Conv2D(64, (3,3), activation='relu'),
  tf.keras.layers.MaxPooling2D(2,2),
  tf.keras.layers.Flatten(),
  tf.keras.layers.Dense(128, activation='relu'),
  tf.keras.layers.Dense(10, activation='softmax')
])
model.compile(optimizer='adam', loss='sparse_categorical_crossentropy', metrics=['accuracy'])
model.summary()
model.fit(training_images, training_labels, epochs=5)
test_loss = model.evaluate(test_images, test_labels)

其结果如下：

Epoch 1/5
60000/60000 [==============================] - 216s 4ms/sample - loss: 0.4520 - acc: 0.8356
Epoch 2/5
60000/60000 [==============================] - 196s 3ms/sample - loss: 0.2985 - acc: 0.8904
Epoch 3/5
60000/60000 [==============================] - 208s 3ms/sample - loss: 0.2525 - acc: 0.9070
Epoch 4/5
60000/60000 [==============================] - 211s 4ms/sample - loss: 0.2236 - acc: 0.9172
Epoch 5/5
60000/60000 [==============================] - 201s 3ms/sample - loss: 0.1953 - acc: 0.9265
10000/10000 [==============================] - 9s 935us/sample - loss: 0.2658 - acc: 0.9051

通过上面的代码及其运行情况，可以得到：

1. 使用优化后的代码，会比之前的代码运行更慢，因为其会涉及把图片进过两次卷积和池化，并且进行64个图片操作；
2. 使用优化后的代码后，明显感觉到其在训练集、验证集的效果会更好。

4. 可视化卷积结果

本节主要是卷积结果的可视化，具体指的是：获取上面的模型，然后同时选择多个图片，以及一个卷积（滤波器矩阵），看模型的四层（第一次卷积、第一次池化、第二次卷积、第二次池化）的输出效果。

先查看 测试数据的部分结果：

print(test_labels[:100])

输出为：

[9 2 1 1 6 1 4 6 5 7 4 5 7 3 4 1 2 4 8 0 2 5 7 9 1 4 6 0 9 3 8 8 3 3 8 0 7
 5 7 9 6 1 3 7 6 7 2 1 2 2 4 4 5 8 2 2 8 4 8 0 7 7 8 5 1 1 2 3 9 8 7 0 2 6
 2 3 1 2 8 4 1 8 5 9 5 0 3 2 0 6 5 3 6 7 1 8 0 1 4 2]

从上面的结果来看下标为0,23，28的图片都是9，也就是shoes，那么一般情况下，卷积可以针对同一类的图片，能发现其共同的特征，使用下面代码：

#%matplotlib
import matplotlib.pyplot as plt
f, axarr = plt.subplots(3,4)
FIRST_IMAGE=0 # 第一个图片下标
SECOND_IMAGE=23# 第二个图片下标
THIRD_IMAGE=28# 第三个图片下标
CONVOLUTION_NUMBER = 1 # 第1个卷积 ,调整卷积为1,2,6 ，可以看到不同图片
from tensorflow.keras import models
layer_outputs = [layer.output for layer in model.layers]
activation_model = tf.keras.models.Model(inputs = model.input, outputs = layer_outputs)
for x in range(0,4):
    f1 = activation_model.predict(test_images[FIRST_IMAGE].reshape(1, 28, 28, 1))[x]
    axarr[0,x].imshow(f1[0, : , :, CONVOLUTION_NUMBER], cmap='inferno')
    axarr[0,x].grid(False)
    f2 = activation_model.predict(test_images[SECOND_IMAGE].reshape(1, 28, 28, 1))[x]
    axarr[1,x].imshow(f2[0, : , :, CONVOLUTION_NUMBER], cmap='inferno')
    axarr[1,x].grid(False)
    f3 = activation_model.predict(test_images[THIRD_IMAGE].reshape(1, 28, 28, 1))[x]
    axarr[2,x].imshow(f3[0, : , :, CONVOLUTION_NUMBER], cmap='inferno')
    axarr[2,x].grid(False)

调整 CONVOLUTION_NUMBER分别为1,2,6，即可看到如下所示图片：

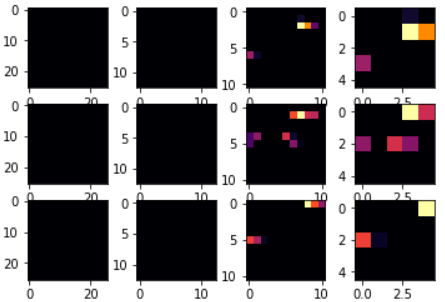
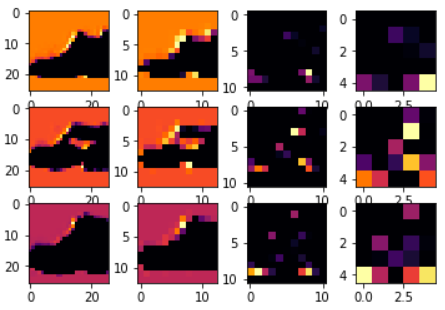
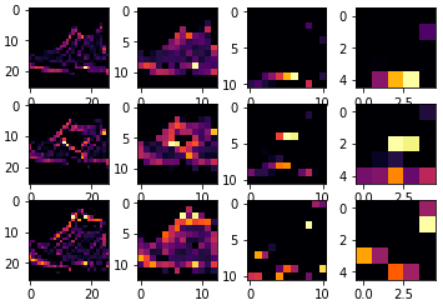
从图片中可以看到：

1. 图片像素从最开始的28*28，变为26*26， -> 13*13 , -> 11*11 ,-> 5*5;
2. 明显可以看出当CONVOLUTION_NUMBER为2时，其特征区分的最好（就3个对比来说）；

使用CONVOLUTION_NUMBER为2，并且调整第二个图片的下标为2，那么可以得到如下图：

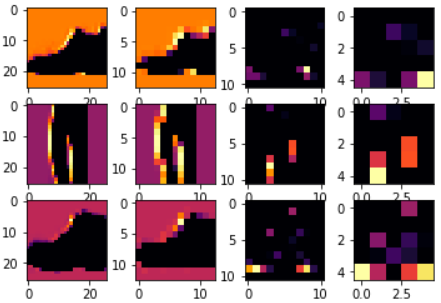
从图上可以看出，使用CONVOLUTION_NUMBER为2的滤波器矩阵，对图片的分类效果比较好，能较明显的区分鞋子和裤子。

5. 纯Python理解卷积和池化

使用如下代码，引入图片：

#%matplotlib
import cv2
import numpy as np
from scipy import misc
i = misc.ascent()

import matplotlib.pyplot as plt
plt.grid(False)
plt.gray()
plt.axis('off')
plt.imshow(i)
plt.show()

图片如下：

获取图片大小：

i_transformed = np.copy(i)
size_x = i_transformed.shape[0]
size_y = i_transformed.shape[1]

定义3*3 filter：

# This filter detects edges nicely
# It creates a convolution that only passes through sharp edges and straight
# lines.

#Experiment with different values for fun effects.
#filter = [ [0, 1, 0], [1, -4, 1], [0, 1, 0]]

# A couple more filters to try for fun!
filter = [ [-1, -2, -1], [0, 0, 0], [1, 2, 1]]
#filter = [ [-1, 0, 1], [-2, 0, 2], [-1, 0, 1]]

# If all the digits in the filter don't add up to 0 or 1, you 
# should probably do a weight to get it to do so
# so, for example, if your weights are 1,1,1 1,2,1 1,1,1
# They add up to 10, so you would set a weight of .1 if you want to normalize them
weight  = 1

应用卷积：

for x in range(1,size_x-1):
  for y in range(1,size_y-1):
      convolution = 0.0
      convolution = convolution + (i[x - 1, y-1] * filter[0][0])
      convolution = convolution + (i[x, y-1] * filter[0][1])
      convolution = convolution + (i[x + 1, y-1] * filter[0][2])
      convolution = convolution + (i[x-1, y] * filter[1][0])
      convolution = convolution + (i[x, y] * filter[1][1])
      convolution = convolution + (i[x+1, y] * filter[1][2])
      convolution = convolution + (i[x-1, y+1] * filter[2][0])
      convolution = convolution + (i[x, y+1] * filter[2][1])
      convolution = convolution + (i[x+1, y+1] * filter[2][2])
      convolution = convolution * weight
      if(convolution<0):
        convolution=0
      if(convolution>255):
        convolution=255
      i_transformed[x, y] = convolution

查看卷积后的结果：

# Plot the image. Note the size of the axes -- they are 512 by 512
plt.gray()
plt.grid(False)
plt.imshow(i_transformed)
#plt.axis('off')
plt.show()   

得到的图如下：

应用池化：

new_x = int(size_x/2)
new_y = int(size_y/2)
newImage = np.zeros((new_x, new_y))
for x in range(0, size_x, 2):
    for y in range(0, size_y, 2):
        pixels = []
        pixels.append(i_transformed[x, y])
        pixels.append(i_transformed[x+1, y])
        pixels.append(i_transformed[x, y+1])
        pixels.append(i_transformed[x+1, y+1])
        pixels.sort(reverse=True)
        newImage[int(x/2),int(y/2)] = pixels[0]

# Plot the image. Note the size of the axes -- now 256 pixels instead of 512
plt.gray()
plt.grid(False)
plt.imshow(newImage)
#plt.axis('off')
plt.show()      
    

查看结果：

从结果可以看出，图片的一些特征是被强化的。

6. 测验：

1. 第 1 个问题
   What is a Convolution?

• a. A technique to filter out unwanted images
• b. A technique to make images bigger
• c. A technique to make images smaller
• d. A technique to isolate features in images

2. 第 2 个问题
   What is a Pooling?

• a. A technique to isolate features in images
• b. A technique to combine pictures
• c. A technique to reduce the information in an image while maintaining features
• d. A technique to make images sharper

3. 第 3 个问题
   How do Convolutions improve image recognition?

• a. They make the image smaller
• b. They make processing of images faster
• c. They make the image clearer
• d. They isolate features in images

4. 第 4 个问题
   After passing a 3x3 filter over a 28x28 image, how big will the output be?

• a. 28x28
• b. 25x25
• c. 26x26
• d. 31x31

5. 第 5 个问题
   After max pooling a 26x26 image with a 2x2 filter, how big will the output be?

• a. 26x26
• b. 28x28
• c. 13x13
• d. 56x56

6. 第 6 个问题
   Applying Convolutions on top of our Deep neural network will make training:

• a. It depends on many factors. It might make your training faster or slower, and a poorly designed Convolutional layer may even be less efficient than a plain DNN!
• b. Stay the same
• c. Faster
• d. Slower

 My Guess:
    1. d
    2. c
    3. d
    4.c
    5. c
    6. a

7. 额外练习：

针对MNIST数据构建的模型进行优化，同时满足如下要求：

1. 提升正确率到99.8%+；
2. 只能使用一个卷积层和一个池化层；
3. 当达到99.8%+的正确率后，立即停止训练（正常情况下20步骤内可以达到），并打印Reached 99.8% accuracy so cancelling training!；

下面是提示代码：

import tensorflow as tf

# YOUR CODE STARTS HERE

# YOUR CODE ENDS HERE

mnist = tf.keras.datasets.mnist
(training_images, training_labels), (test_images, test_labels) = mnist.load_data()

# YOUR CODE STARTS HERE

# YOUR CODE ENDS HERE

model = tf.keras.models.Sequential([
    # YOUR CODE STARTS HERE

    # YOUR CODE ENDS HERE
])

# YOUR CODE STARTS HERE

# YOUR CODE ENDS HERE

Answer

Code Download Here