Scalar-multiplication算法集
Posted mutourend
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了Scalar-multiplication算法集相关的知识,希望对你有一定的参考价值。
1. 引言
ECC金字塔:
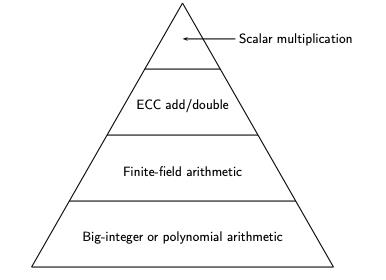
该金字塔层级之间不是独立的。
scalar multiplication针对的为:
- (finite, abelian)group G G G,为加法群,计算 k ⋅ P k\\cdot P k⋅P,其中 k ∈ Z , P ∈ G k\\in \\mathbbZ,P\\in G k∈Z,P∈G。
- 而对于乘法群 G ′ G' G′,等价为计算 x k x^k xk,其中 x ∈ G ′ x\\in G' x∈G′。
加法群的scalar multiplication 与 乘法群的幂运算,二者算法等价。
Scalar-multiplication广泛用于多种密码学场景中:
- 基于ECDLP的密钥生成
- EC Diffie-Hellman密钥交换
- Schnorr签名
这些场景中都需要计算
k
P
kP
kP。
进一步观察可发现:
- 密钥生成时,点 P P P在编译时是固定的。
- Diffie-Hellman密钥交换时,联合密钥计算时的点是在运行时收到的。
- Schnorr签名验签时,需要double-scalar multiplication k 1 P 1 + k 2 P 2 k_1P_1+k_2P_2 k1P1+k2P2。Schnorr签名验签时的scalar值 k 1 , k 2 k_1,k_2 k1,k2是public的。
以上场景中,存在secret scalar和public scalar的差异:
- 无论 k k k是secret scalar还是public scalar值,计算 k P kP kP的结果应完全相同。
不过在scalar multiplication中需考虑Timing信息问题:
- 某些快速scalar-multiplication算法其运行时长与 k k k值相关。
- 攻击者可测量时长来推断 k k k的信息。
- 如Brumley, Tuveri, 2011:数分钟即可窃取网络中TLS服务的私钥。
因此,当 k k k为secret scalar时,相应的scalar multiplication算法应为constant-time的。
1.1 基于ECDLP的密钥生成
所谓ECDLP(基于椭圆曲线的DLP)为:
已知椭圆曲线上2个点
P
和
Q
P和Q
P和Q,
Q
∈
<
P
>
Q\\in <P>
Q∈<P>,找到某整数
k
k
k,使得
k
P
=
Q
kP=Q
kP=Q成立。
密码学系统的经典设定为:
- P P P为某固定的系统参数
- k k k为私钥
- Q Q Q为公钥
已知 k 和 P k和P k和P,密钥生成实际是计算 Q = k P Q=kP Q=kP。
1.2 EC Diffie-Hellman密钥交换
EC Diffie-Hellman密钥交换针对的场景为:
- 用户Alice和Bob分别具有密钥对 ( k A , Q A ) 和 ( k B , Q B ) (k_A,Q_A)和(k_B,Q_B) (kA,QA)和(kB,QB)。
- Alice将其公钥 Q A Q_A QA发送给Bob
- Bob将其公钥 Q B Q_B QB发送给Alice
- Alice计算联合密钥 K = k A Q B K=k_AQ_B K=kAQB
- Bob计算联合密钥 K = k B Q A K=k_BQ_A K=kBQA
1.3 Schnorr签名
Schnorr签名的场景为:
- Alice的密钥对为 ( k A , Q A ) (k_A, Q_A) (kA,QA)
- 基点 < P > <P> <P>的order为 l l l
- 采用的密码学哈希函数为 H H H
Schnorr签名过程为:
- Alice(签名者)生成密码随机值
r
∈
1
,
⋯
,
l
r\\in\\1,\\cdots,l\\
r∈1,⋯,l,对于消息
m
m
m进行如下计算获得签名
(
R
,
s
)
(R,s)
(R,s):
- 计算 R = r P R=rP R=rP
- 计算 s = ( r − H ( R , m , Q A ) k A ) m o d l s=(r-H(R,m,Q_A)k_A)\\mod l s=(r−H(R,m,QA)kA)modl
任何具有Alice公钥 Q A Q_A QA的人,都可对消息 m m m的签名 ( R , s ) (R,s) (R,s)进行验签,验签过程为:
- 验证 R = s P + H ( R , m , Q A ) Q A R=sP+H(R,m,Q_A)Q_A R=sP+H(R,m,QA)QA成立,即验签通过。
2. Scalar-multiplication算法演变
以计算 105 ⋅ P 105\\cdot P 105⋅P为例:
- 直观的算法是,直接做104次加法运算: P + P + P + ⋯ + P P+P+P+\\cdots +P P+P+P+⋯+P
但是, 105 105 105约有7个bits,需要约 2 7 2^7 27次加法运算。实际真实的scalar值约有 256 256 256个bits,若采用这种直观算法,需要约 2 256 2^256 2256次加法运算(比解决ECDLP还昂贵)。
为此,我们需要scalar-multiplication算法的运行时长为与scalar size呈polynomial time关系的。
将
105
105
105表示为:
105
=
64
+
32
+
8
+
1
=
2
6
+
2
5
+
2
3
+
2
0
105=64+32+8+1=2^6+2^5+2^3+2^0
105=64+32+8+1=26+25+23+20
进一步表示为: 以上是关于Scalar-multiplication算法集的主要内容,如果未能解决你的问题,请参考以下文章
105
=
1
⋅
2
6
+
1
⋅
2
5
+
0
⋅
2
4
+
1
⋅
2
3
+
0
⋅
2
2
+
0
⋅
2
1
+
1
⋅
2
0
105=1\\cdot 2^6+1\\cdot 2^5+0\\cdot 2^4+1\\cdot 2^3+0\\cdot 2^2+0\\cdot 2^1+1\\cdot 2^0
105=1⋅26+1⋅25+0⋅24+1⋅23+0⋅22+<