聚类算法(无监督学习)
Posted 别团等shy哥发育
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了聚类算法(无监督学习)相关的知识,希望对你有一定的参考价值。
聚类
1、聚类概述
1.1 什么是聚类
聚类就是把数据对象集合按照相似性划分成多个子集的过程(如下图)。其中,每个子集称为一个簇。聚类不仅要使簇中的对象彼此相似,而且要与其他簇中的对象相似。聚类是无监督学习,数据不需要类标号(标注)信息。

聚类分析以相似度为基础,在一个聚类中的模式比不在这个聚类中的模式有更多的相似度。
1.2 分类与聚类
分类是有监督学习,即每个训练样本的数据对象已经有类标签,通过有标签样本学习分类器。
聚类是无监督学习,即不使用训练数据进行学习,通过观察学习将数据集分割成多个簇。
1.3 聚类的应用
- 商业领域:聚类分析用于发现不同的客户群,并且通过购买模式刻画不同客户群的特征。
- 电子商务:聚类出具有相似浏览行为的客户,并分析客户的共同特征,可以更好地帮助电子商务的用户了解自己的客户,向客户提供更合适的服务。
- 舆情监控:发现热点、主体、话题、事件,发现未知异常等。
2、基本的聚类方法
2.1 划分方法
2.1.1 划分方法概述
划分方法是指讲有n个对象的数据集D划分成k(k<=n)个簇,需满足两个条件:
- 每个簇至少包含一个对象
- 每个对象属于且仅属于一个簇。
其基本思想是首先创建一个初始k划分(k为要构造的划分数),然后不断迭代计算各个簇的聚类中心,并依据新的聚类中心调整聚类情况,直至收敛。
划分方法的目标有两个:
- 同一个簇中的对象之间尽可能“接近”或相关
- 不同簇中的对象尽可能“原理”或不同。
启发式方法有两种:
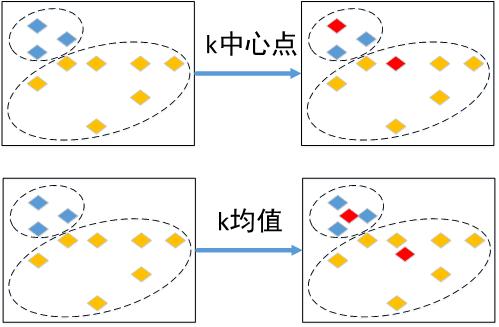
- K均值(K-Means),每个簇用该簇中对象的均值来表示,为基于质心的技术。
- K中心点(K-Medoids),每个簇用接近簇中心的一个对象来表示,为基于代表对象的技术。
这些启发式算法适合发现中小规模数据库中的球状聚类;对于大规模数据库和处理任意形状的聚类,这些算法还需要进一步扩展。
2.1.2 K-Means算法
K-Means算法是启发式算法,遵循寻优原则(如下图),即每次聚类保证局部最优,随后调整聚类,利用局部最优聚类的上限来不断逼近全局最优。
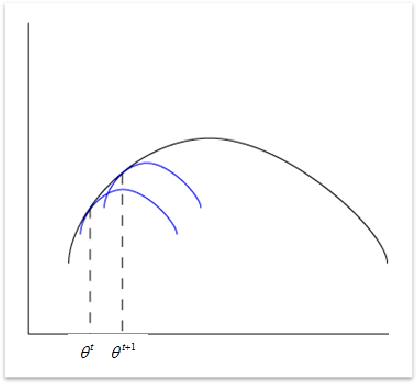
具体算法步骤如下:
- (1)从数据集中随机取K个样本作为初始的聚类中心 C = c 1 , c 2 , . . . , c k C=c_1,c_2,...,c_k C=c1,c2,...,ck。
- (2)针对数据集中的每个样本 x i x_i xi,计算它到K个聚类中心的距离并将其分到距离最小的聚类中心对应的类中。
- (3)针对每个类别 C i C_i Ci,重新计算其聚类中心 c i = 1 ∣ c i ∣ ∑ x ∈ c i x c_i=\\frac1\\left | c_i \\right | \\sum_x\\in c_i ^x ci=∣ci∣1∑x∈cix
- (4)重复第2步和第3步,直到 ∑ i = 0 n m i n c j ∈ C ( ∥ x j − c i ∥ 2 ) \\sum_i=0^n\\undersetc_j\\in C min(\\left \\| x_j-c_i \\right \\|^2 ) ∑i=0ncj∈Cmin(∥xj−ci∥2)
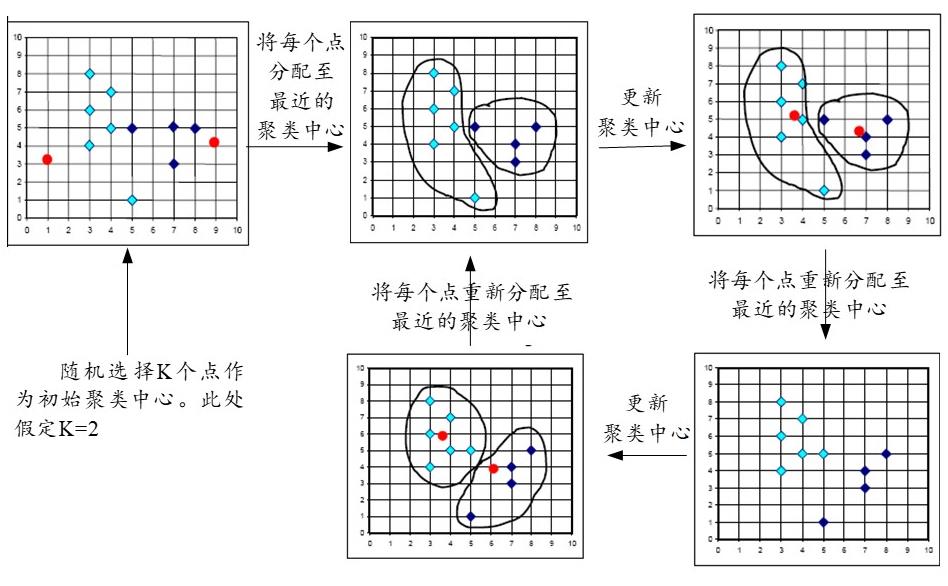
2.1.3 K-means计算实例
例1:给定如下要进行聚类的对象:2,4,10,12,3,20,30,11,25,K= 2,请使用K均值划分聚类。具体计算步骤如下:
| m 1 m_1 m1 | m 2 m_2 m2 | K 1 K_1 K1 | K 2 K_2 K2 |
|---|---|---|---|
| 2 | 4 | 2,3 | 4,10,12,20,30,11,25 |
| 2.5 | 16 | 2,3,4 | 10,12,20,30,11,25 |
| 3 | 18 | 2,3,4,10 | 10,12,20,30,11,25 |
| 4.75 | 19.6 | 2,3,4,10,11,12 | 20,30,25 |
| 7 | 25 | 2,3,4,10,11,12 | 20,30,25 |
例2:假定我们对A、B、C、D四个样品分别测量两个变量和得到结果见表。试将表中得样品聚成两类。

第一步:按要求取K=2,为了实施均值法聚类,我们将这些样品随意分成两类,比如(A、B)和(C、D),然后计算这两个聚类的中心坐标,见下表所示。
中心坐标是通过原始数据计算得来的。

第二步:计算某个样品到各类中心的欧氏平方距离,然后将该样品分配给最近的一类。对于样品有变动的类,重新计算它们的中心坐标,为下一步聚类做准备。先计算A到两个类的平方距离:
d
2
(
A
,
(
A
B
)
)
=
(
5
−
2
)
2
+
(
3
−
2
)
2
=
10
d
2
(
A
,
(
C
D
)
)
=
(
5
+
1
)
2
+
(
3
+
2
)
2
=
61
d^2(A,(AB))=(5-2)^2+(3-2)^2=10\\\\ d^2(A,(CD))=(5+1)^2+(3+2)^2=61
d2(A,(AB))=(5−2)2+(3−2)2=10d2(A,(CD))=(5+1)2+(3+2)2=61
由于A到(A、B)的距离小于到(C、D)的距离,因此A不用重新分配。计算B到两类的平方距离:
d
2
(
B
,
(
A
B
)
)
=
(
−
1
−
2
)
2
+
(
1
−
2
)
2
=
10
d
2
(
B
,
(
C
D
)
)
=
(
−
1
+
1
)
2
+
(
1
+
2
)
2
=
9
d^2(B,(AB))=(-1-2)^2+(1-2)^2=10\\\\ d^2(B,(CD))=(-1+1)^2+(1+2)^2=9
d2(B,(AB))=(−1−2)2+(1−2)2=10d2(B,(CD))=(−1+1)2+(1+2)2=9
由于B到(A、B)的距离大于到(C、D)的距离,因此B要分配给(C、D)类,得到新的聚类是(A)和(B、C、D)。 更新中心坐标如下表所示。
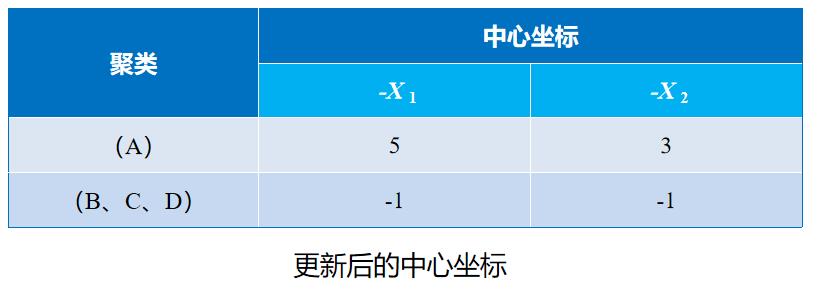
第三步:再次检查每个样品,以决定是否需要重新分类。计算各样品到各中心的距离平方,结果见下表。
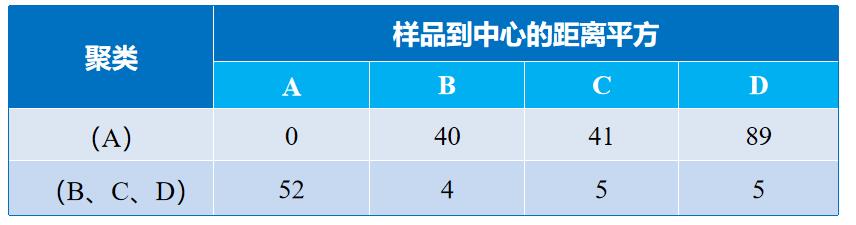
到现在为止,每个样品都已经分配给距离中心最近的类,因此聚类过程到此结束。最终得到K=2的聚类结果是A独自成 一类,B、C、D聚成一类。
2.1.4 K-means改进算法
(1)K-Mode算法
- 用众数代替平均数
- 使用新的相异性度量。
(2)K-means++算法
通过尽可能选择距离远得点作为初始种子节点,从而解决K-means初始点选择问题。具体得算法流程如下:
- 从输入的数据点集合中随机选择一个点作为第一个聚类中心
- 对于数据集中的每一个点X,计算其与聚类中心的距离D(X)
- 选择一个D(X)最大的点作为新的聚类中心
- 重复2和3步直到K个聚类中心被选出
- 利用K个初始聚类中心运行K-Means
(3)K中心点(K-Mediods)算法
K中心点主要通过选用簇中位置最中心的实际对象即中心点作为参照点并基于最小化所有对象与其参照点之间的相异度之和 E = ∑ i = 1 k ∑ p ∈ C i ∣ p − o i ∣ E=\\sum_i=1^k\\sum_p\\in C_i^ \\left |p-o_i \\right | E=∑i=1k∑p∈Ci∣p−oi∣划分(使用绝对误差标准),解决离群点敏感问题。
2.2 层次方法
2.1.1 层次方法概述
层次方法满足三个条件:
- 对给定数据对象集进行层次的分解
- 使用距离矩阵作为聚类标准
- 不需要输入聚类数目k,但需要终止条件
有两种层次方法:
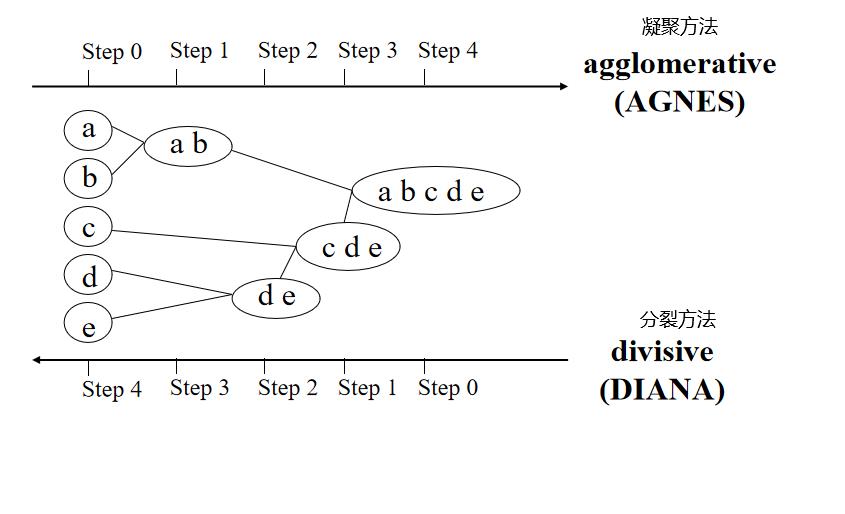
- (1) 自底向上方法(凝聚):初始将每个对象作为单独的一个簇,然后相继的合并相近的对象或簇,直到所有的簇合并为一个,或者达到一个终止条件。代表算法:AGNES算法
- (2) 自顶向下方法(分裂):初始将所有的对象置于一个簇中,在迭代的每一步,一个簇被分裂为多个更小的簇,直到最终每个对象在一个单独的簇中,或达到一个终止条件。代表算法:DIANA算法
3、基于密度的方法
3.1 相关概念
基于密度聚类是指根据密度条件对邻近对象分组形成簇,簇的增长或者根据邻域密度,或者根据特定的密度函数(只要临近区域的密度超过某个阈值,就继续聚类)
主要特点:
- 发现任意形状的聚类
- 处理噪音
- 一边扫面
- 需要密度参数作为终止条件。
ε-邻域:给定对象半径ε内的邻域称为该对象的ε-邻域。

核心对象:如果对象的ε-邻域至少包含最小数目MinPts个对象,则称该对象为核心对象
直接密度可达:给定对象集合D,如果p 是在q 的ε-邻域内,而q 是核心对象,则称对象p 是从对象q 关于ε和MinPts直接密度可达的。

密度可达:如果存在一个对象链 p 1 , . . . , p n , p 1 = q , p n = p p_1,...,p_n,p_1=q,p_n=p p1,...,pn,p1=q,pn=p,使得 p i + 1 p_i+1 pi+1是从 p i p_i pi直接密度可达的,则称对象p是从对象q关于ε和MinPts(间接)密度可达的.
密度相连:如果存在对象o 使得,p 和q 都是从o关于ε和MinPts密度可达的,则称对象p与q关于ε和MinPts是密度相连的

4、聚类评估
聚类评估旨在估计在数据集上进行聚类的可行性和被聚类方法产生的结果的质量。主要包括:估计聚类趋势、确定数据集中的簇数、测定聚类质量。
4.1 估计聚类趋势
对于给定的数据集,聚类趋势估计确定给定的数据集是否具有可以得到有意义的聚类的非随机结构。如果数据服从均匀分布,显然对其进行的聚类操作都是没有意义的。
霍普金斯统计量是一种空间统计量,可以检验空间分布的变量的空间随机性。
4.2 确定数据集中的簇数
K均值这样的算法需要数据集的簇数作为参数,簇数也可以看作数据集的一个重要的概括度量,因此,在使用聚类算法导出详细的簇之前,估计簇数是可取的。
- 实验方法:对于n个点的数据集,簇数
n
2
\\sqrt\\fracn2
2n,每个簇约有
以上是关于聚类算法(无监督学习)的主要内容,如果未能解决你的问题,请参考以下文章