路径规划基于matlab Dijkstra算法多机器人路径规划含Matlab源码 1883期
Posted 海神之光
tags:
篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了路径规划基于matlab Dijkstra算法多机器人路径规划含Matlab源码 1883期相关的知识，希望对你有一定的参考价值。
一、Dijkstra算法机器人编队路径规划简介
1 传统Dijkstra算法步骤
Dijkstra算法是一种经典的求解最短路径的算法，用于计算一个节点去往其他各个不相关节点的最小移动代价。本思想是把在图中无论如何出现的所有节点分离为2组，第1组包含被准确认定是最短路径的节点，第2组存放待检查的不确定的节点。根据最小移动代价逐渐增大的顺序，逐个将第2组需要检查的节点加入到第1组中，一直到从起始点出发可以到达的所有节点都包含在第1组中。Dijkstra算法运行的主要特征是以机器人抽象的出发点为中心向外层层延伸，直到延伸到整个区域的末端为止。Dijkstra算法一般能够在最终得到最优的路径，但是这个路径偶尔会出现冗余拐点，由于其遍历节点多，所以有时算法的效率不高。Dijkstra算法流程如图2所示。
分别创建2个表，为：START与FINISH。START表中存放环境中已经生成存在但是未经计算的节点，FINISH表中存放所有经过计算考察的节点。
(1）观测寻找在环境路网中离起始源点近而且是没有被计算过的点，把满足调节的点放在START数组中等待检查。
(2）从START表中找出距离起始点最小的点，然后把该点放进FINISH表中。
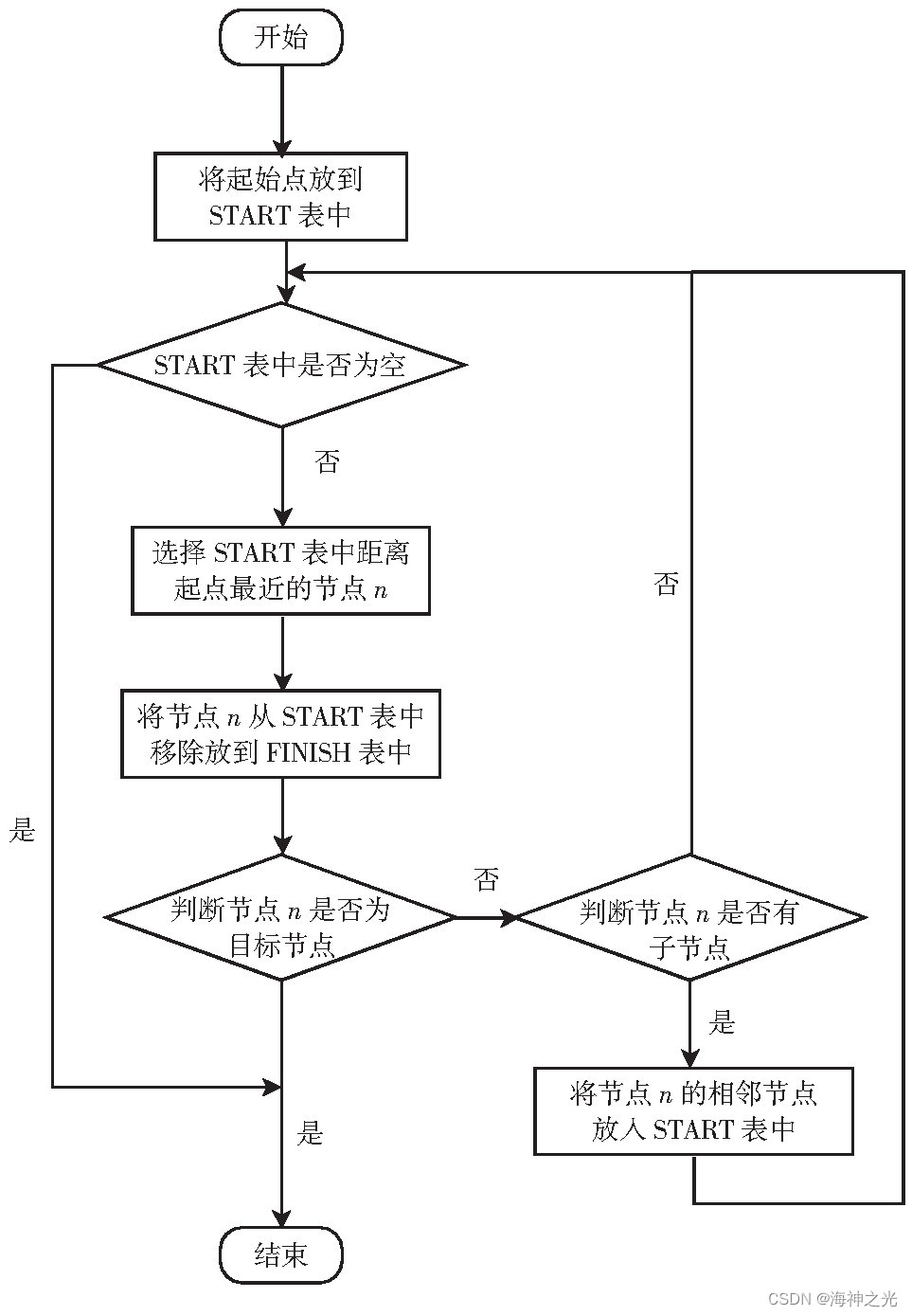
(3）遍历去寻找考察当前此点的子节点，计算出起始源点到这些子节点的距离值，将值存入数组中用来排序，将子节点放在START表中。
(4）重复（2）和（3），直到把START表中的点全部清空，或者找到真正要去的目标点。
2 Dijkstra算法的思想
(1）将环境可视图中出现的节点或是顶点分别加入2个组，其中一组存放经过求解验证为最短路径所经过的顶点，该集合用FINISH表示，刚开始时START表中只有1个起始点，在后面的运算过程中每得到1条最短路径，就把相关节点加入到集合FINISH中。如果全部的顶点都加入到FINISH后，此算法运算完成。另一组存放未经过考察且还未被认定为最短路径的顶点，用START表示。
(2）在将顶点逐渐加入到FINISH表的过程中，在运行算法期间总保持从出发点到FINISH表中各个点的最短路径的长度不超过出发点到START表中任何顶点的最短路径长度。
典型的Dijkstra算法在寻找最优路径的准则上较为单一，以某一个点为中心向外层层扩展就类似于画圆，随着搜索半径的逐渐增大，最后总能找到想要的目标点，但同时最优路径会出现一些无关的冗余点，这样在一定程度上给实际的移动机器人造成寻找路径的困难。如果能够对经典算法的计算准则进行优化，达到减少路径中拐点的目的，就可以减少一大部分机器人寻路所耗费的时间。在大面积环境中使用Dijkstra算法时，由于每次都要从START列表中挑选离原始点最近的点，这样导致规划效率不高，在排序过程消耗很多不必要的工作时间。
二、部分源代码
%define a map
close all ; clear all ;
map = false(14) ;
map(3,3:4) = true ; map(3,7:8) = true ; map(3,11:12) = true ;
map(4,3:4) = true ; map(4,7:8) = true ; map(4,11:12) = true ;
map(7,3:4) = true ; map(7,7:8) = true ; map(7,11:12) = true ;
map(8,3:4) = true ; map(8,7:8) = true ; map(8,11:12) = true ;
map(11,3:4) = true ; map(11,7:8) = true ; map(11,11:12) = true ;
map(12,3:4) = true ; map(12,7:8) = true ; map(12,11:12) = true ;
%define the weight of node
weight = [0 1 0 0; 0 1 0 1; 0 1 0 0; 0 1 0 0; 0 1 0 0; 0 1 0 1; 0 1 0 0; 0 1 0 0; 0 1 0 0; 0 1 0 1; 0 1 0 0; 0 1 0 0; 0 1 0 0; 0 0 0 1;%第一列
0 0 1 0; 1 0 0 1; 1 0 0 0; 1 0 0 0; 1 0 1 0; 1 0 0 1; 1 0 0 0; 1 0 0 0; 1 0 1 0; 1 0 0 1; 1 0 0 0; 1 0 0 0 ;1 0 1 0 ; 1 0 0 1; %第二列
0 0 1 0; 0 0 0 1; 0 0 0 0; 0 0 0 0; 0 0 1 0; 0 0 0 1; 0 0 0 0; 0 0 0 0; 0 0 1 0; 0 0 0 1; 0 0 0 0; 0 0 0 0; 0 0 1 0; 0 0 0 1;%第三列
0 0 1 0; 0 0 0 1; 0 0 0 0; 0 0 0 0; 0 0 1 0; 0 0 0 1; 0 0 0 0; 0 0 0 0; 0 0 1 0; 0 0 0 1; 0 0 0 0; 0 0 0 0; 0 0 1 0; 0 0 0 1;%第四列
0 1 1 0; 0 1 0 1; 0 1 0 0; 0 1 0 0; 0 1 1 0; 0 1 0 1; 0 1 0 0; 0 1 0 0; 0 1 1 0; 0 1 0 1; 0 1 0 0; 0 1 0 0; 0 1 1 0; 0 0 0 1;%第五列
0 0 1 0; 1 0 0 1; 1 0 0 0; 1 0 0 0; 1 0 1 0; 1 0 0 1; 1 0 0 0; 1 0 0 0; 1 0 1 0; 1 0 0 1; 1 0 0 0; 1 0 0 0; 1 0 1 0; 1 0 0 1;%第六列
0 0 1 0; 0 0 0 1; 0 0 0 0; 0 0 0 0; 0 0 1 0; 0 0 0 1; 0 0 0 0; 0 0 0 0; 0 0 1 0; 0 0 0 1; 0 0 0 0; 0 0 0 0; 0 0 1 0; 0 0 0 1;%第七列
0 0 1 0; 0 0 0 1; 0 0 0 0; 0 0 0 0; 0 0 1 0; 0 0 0 1; 0 0 0 0; 0 0 0 0; 0 0 1 0; 0 0 0 1; 0 0 0 0; 0 0 0 0; 0 0 1 0; 0 0 0 1;%第八列
0 1 1 0; 0 1 0 1; 0 1 0 0; 0 1 0 0; 0 1 1 0; 0 1 0 1; 0 1 0 0; 0 1 0 0; 0 1 1 0; 0 1 0 1; 0 1 0 0; 0 1 0 0; 0 1 1 0; 0 0 0 1;%第九列
0 0 1 0; 1 0 0 1; 1 0 0 0; 1 0 0 0; 1 0 1 0; 1 0 0 1; 1 0 0 0; 1 0 0 0; 1 0 1 0; 1 0 0 1; 1 0 0 0; 1 0 0 0; 1 0 1 0; 1 0 0 1;%第十列
0 0 1 0; 0 0 0 1; 0 0 0 0; 0 0 0 0; 0 0 1 0; 0 0 0 1; 0 0 0 0; 0 0 0 0; 0 0 1 0; 0 0 0 1; 0 0 0 0; 0 0 0 0; 0 0 1 0; 0 0 0 1;%第十一列
0 0 1 0; 0 0 0 1; 0 0 0 0; 0 0 0 0; 0 0 1 0; 0 0 0 1; 0 0 0 0; 0 0 0 0; 0 0 1 0; 0 0 0 1; 0 0 0 0; 0 0 0 0; 0 0 1 0; 0 0 0 1;%第十二列
0 1 1 0; 0 1 0 1; 0 1 0 0; 0 1 0 0; 0 1 1 0; 0 1 0 1; 0 1 0 0; 0 1 0 0; 0 1 1 0; 0 1 0 1; 0 1 0 0; 0 1 0 0; 0 1 1 0; 0 0 0 1;%第十三列
0 0 1 0; 1 0 0 0; 1 0 0 0; 1 0 0 0; 1 0 1 0; 1 0 0 0; 1 0 0 0; 1 0 0 0; 1 0 1 0; 1 0 0 0; 1 0 0 0; 1 0 0 0; 1 0 1 0; 1 0 0 0;%第十四列
] ;
%start point array and destination point array
start_coords_array = [6,2; 1,1; 5,9; 9,14; 5,8; 12,10; 14,7; 3,14; 1,9; 14,10 ];
dest_coords_mark_array =[9 3 2 8 3 1 3 4 5 3];
FLAG = zeros(1, 10);
[map_color, route, dest_node] = multi_path_generation( start_coords_array, dest_coords_mark_array, map, weight);
%初始化机器人开始的位置并且显示出来
for j = 1:10
robot_color = 16+j;
map_color(route(j, 1)) = robot_color;
end
image(1.5, 1.5, map_color);
grid on;
axis image;
pause(0.5);
for i = 1:100
for j = 1:10
robot_color = 16+j;
if (route(j, i+1)) %如果未达到终点
[exist_robot, collision_robot_index, is_dest_node] = detect_robot_state(map_color, dest_coords_mark_array, route, [j, i], dest_node);
if (~exist_robot) %如果路径可行，则直接移动到下一个路径点
map_color(route(j, i+1)) = robot_color;
map_color(route(j, i)) = 1;
else %否则路径上存在机器人
if (is_dest_node) %如果机器人在终点，则进行“绕桌”行为
%障碍物机器人绕桌
[route, dest_node] = desk_surround(map, route, collision_robot_index, j, i, dest_node, dest_coords_mark_array);
%当前机器人等待
[nrows, ncols] = size(route);
route(j, 1:ncols+1) = add_path_point(route(j, :), route(j, i),i+1);
map_color(route(j, i+1)) = robot_color;
else %如果障碍物不在终点，当前机器人等待即可
%当前机器人等待
[nrows, ncols] = size(route);
route(j, 1:ncols+1) = add_path_point(route(j, :), route(j, i),i+1);
map_color(route(j, i+1)) = robot_color;
end
end
else %如果已经达到终点,原地等待，并且添加一个FLAG
[nrows, ncols] = size(route);
route(j, 1:ncols+1) = add_path_point(route(j, :), route(j, i),i+1);
map_color(route(j, i+1)) = robot_color;
FLAG(j) = 1;
end
%显示过程
image(1.5, 1.5, map_color);
grid on;
axis image;
pause(0.01);
%终止条件
if FLAG == ones(1, 10)
disp(route');
success = true;
[row, col] = size(route);
for n = 1:col
if route(以上是关于路径规划基于matlab Dijkstra算法多机器人路径规划含Matlab源码 1883期的主要内容，如果未能解决你的问题，请参考以下文章
路径规划基于matlab A_star算法智能仓储机器人移动避碰路径规划含Matlab源码 1180期
Dijkstra算法A*算法D*算法LPA*算法和D* Lite算法详解汇总（原理matlab代码）格栅地图