归纳总结MATLAB中与矩阵运算有关的算术运算符(加减乘除点乘点除乘方转置等)

Posted 2022-06-14 昊虹图像算法

运算是算法的基础，所以我们有必要了解我们使用的工具怎样实现矩阵的基本运算。

这篇博文总结MATLAB中矩阵的算术运算符。

目录

• 01-加法运算符“+”
• 02-减法(相反数)运算符“-”
• 03-元素乘积(点乘)运算符“.*”
• 04-元素右除(点除)运算符“./”
• 05-元素左除(点除)运算符“.\\”
• 06-元素乘方运算符“.^”
• 07-转置运算符“.'”和运算符“ ' ”
• 08-矩阵乘法运算符“*”
• 09-矩阵除法运算符“/”和运算符“\\”(注意:这个和元素的左右除法很不一样)
• 10-矩阵乘方运算符“^”

01-加法运算符“+”

A+B表示把矩阵A和B的对应元素相加，A和B必须是具有相同尺寸的矩阵，除非它们之一为标量。
此种情况的第一个示例如下(A、B皆为相同尺寸的矩阵)：

A = [1 2 3;4 5 6;7 8 9];
B = [2 3 4;5 6 7;8 9 0];
C = A+B;

运行结果：



此种情况的第二个示例如下(A、B中一个为矩阵，一个为标量)：

A = [1 2 3;4 5 6;7 8 9];
b = 5;
C = A+b;

02-减法(相反数)运算符“-”

A-B表示把矩阵A与矩阵B中的对应元素进行相减运算。A和B必须是具有相同尺寸的矩阵，除非它们之一为标量。运算符“-”还可以求矩阵中每个元素的相反数。
运算符“-”的第一个示例代码(A、B均为矩阵)

A = [1 2 3;4 5 6;7 8 9];
B = [2 3 4;5 6 7;8 9 0];
C = B-A;

运算符“-”的第二个示例代码(A、B中一个为矩阵，一个为标量)

A = [1 2 3;4 5 6;7 8 9];
b = 2;
C = b-A;
D = A-b;

运算符“-”的第三个示例代码(求矩阵中每一个元素的相反数)

A = [1 2 3;4 5 6;7 8 9];
B = -A;

运行结果如下：

03-元素乘积(点乘)运算符“.*”

功能：A.*B相当于矩阵A和矩阵B对应的元素相乘，A和B必须是具有相同尺寸的矩阵，除非它们之一为标量。
运算符“.*”的第一个示例代码：

A = [1 2 3;4 5 6;7 8 9];
B = [2 3 4;5 6 7;8 9 0];
C = A.*B;

运行结果：

运算符“.*”的第二个示例代码：

A = [1 2 3;4 5 6;7 8 9];
b = 3;
C = A.*b;
D = b.*A;

运行结果如下：

04-元素右除(点除)运算符“./”

功能：运算符“./”是元素的右除法，A./B的意思为A矩阵中的元素除以B矩阵中的对应元素，A和B必须是具有相同尺寸的矩阵，除非它们之一为标量。
运算符“./”的第一个示例代码如下：

B = [1 2 3;4 5 6;7 8 9];
A = [2 6 12;20 30 42;56 72 90];
C = A./B;

运行结果如下：



运算符“./”的第二个示例代码如下：

A = [3 6 9;12 15 18;21 24 27];
b = 3;
C = A./b;

运行结果如下：

05-元素左除(点除)运算符“.\\”

运算符“.\\”为元素的左除法，这个运算符和运算符“./”的使用方法相同，只不过是把被除数和除数的位置换一下，即A.\\B的意思为B矩阵中的元素除以A矩阵中的对应元素，A和B必须是具有相同尺寸的矩阵，除非它们之一为标量。
示例略！

06-元素乘方运算符“.^”

作用：运算符“.^”为矩阵中元素的乘方。A.^B的意思为A中的元素为底数，B中对应的元素为指数作乘方运算。同样A和B必须是具有相同尺寸的矩阵，除非它们之一为标量。
运算符“.^”的示例代码如下：

A = [1 2 3;4 5 6;7 8 9];
B = [9 8 7;6 5 4;3 2 1];
C = A.^B;

运行结果如下：

07-转置运算符“.'”和运算符“ ’ ”

运算符“.'”和运算符“ ’ ”都用于求矩阵的转置，区别在于对复数矩阵的处理，前者在求复数矩阵的转置时，不对每个元素求其共轭复数，后者在求复数矩阵的转置时，会对每个元素求其共轭复数。
示例代码如下：

A = [1 2 3;4 5 6];
B = A.';
C = A';

D = [1+2i 3+4i 5+6i];
E = D.';
F = D';

运行结果如下：

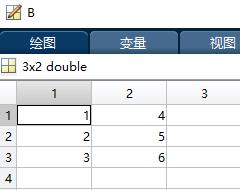
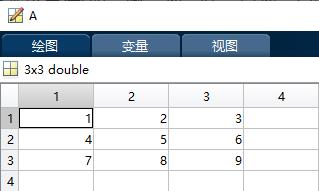
08-矩阵乘法运算符“*”

作用：A*B表示矩阵A和矩阵B的乘法，当A和B均为矩阵时，根据矩阵乘法的运算规则，A的列数需要和B的行数相等。如果不想满足这个条件而使用这个运算符，除非它们之一为标量，此时有A*b=A.*b
示例代码如下：

A = [1 2 3;4 5 6];
B = [7 8;9 10;11 12];
C = A*B;

b = 3;
D = A*b;
F = A.*b;

运行结果如下：

09-矩阵除法运算符“/”和运算符“\\”(注意:这个和元素的左右除法很不一样)

运算符“/”和运算符“\\”的作用是矩阵右除法矩阵左除法。我们知道矩阵其实是没有除法的定义的，在线性代数中与之相关的概念是矩阵的逆。
那么A\\B和B/A分别代表什么呢？
不考虑结果精度的话：A\\B相当于 inv(A)*B
不考虑结果精度的话：B/A相当于 B*inv(A)
这里要特别注意：A\\B并不像元素除法那样等于B/A，规律是被斜线压在下方的那个矩阵作求逆运算。
示例和验证代码如下：

A = [1 2;3 4];
B = [5 6;7 8];

C = A\\B;
E = inv(A)*B;

D = B/A;
F = B*inv(A);

运行结果如下：


可见C和E的结果是一样的，说明A\\B相当于inv(A)*B


可见D和F的结果是一样的，说明B/A相当于 B*inv(A)

10-矩阵乘方运算符“^”

运算符“^”是矩阵的乘方运算，注意在式子A^B中，A和B是不能同时为矩阵，具体用法如下：
当A和B都是标量时，表示标量A的B次方。
当A为方阵，B为正整数时，表示矩阵A的B次乘积；
当A为方阵，B为负整数时，表示矩阵A的逆的B次乘积；
当B为非整数时，有如下表达式：

运算符“^”的示例代码就不贴了。