“正交阵”与“特征值和特征向量”
Posted 血影雪梦
tags:
篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了“正交阵”与“特征值和特征向量”相关的知识，希望对你有一定的参考价值。
正交阵
概念：若n阶矩阵A满足ATA=I，则A为正交矩阵，简称正交阵。
ATA=I解释的话就是：
“A的第i行”*“A的第i列”= 1
“A的第i行”*“A的非第i列”= 0。
其他：
1，A是正交阵，x为向量，则A·x称作正交变换；
正交变换不改变向量长度。
如：
A=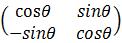 
，PS：这是个正交阵
B= (x0, y0)，PS：B是映射到x，y坐标轴上的一个点
于是A·BT的结果就是让B这个点在坐标上逆时针旋转°。
2，A、B都是n阶正交阵，那么A*B是正交阵。
特征值和特征向量
定义：A是n阶矩阵，若数λ和n维非0列向量x满足Ax=λx，那么，数λ称为A的特征值，x称为A的对应于特征值λ的特征向量。
解释：
Ax=λx意味着：Ax正好是列向量x的λ倍，即：向量x乘上矩阵A的结果仅仅是改变向量x的长度。那么，这个x和A一定有着某种联系（因为x被A作用之后x的方向压根就没变），就好像很多故事中将保护公主的人称为骑士一样(公主和骑士是有联系的)，那这里就把这个x称作A的特征向量。
OK，等号左边至少可以理解了吧，然后为了描述等号右边，就把λ称作特征向量x的特征值。
PS：上学时我们经常这样求解特征值和特征向量：
根据定义，立刻得到(A-λI)x= 0，令关于λ 的多项式|A-λI|为0，方程|A-λI|=0的根为A的特征值；将根λ带入方程组(A-λI)x = 0 ，求得到的非零解，即λ对应的特征向量。
不过，虽然这样能解，但这样没啥实际价值。实践中一般使用Q·R分解。
性质：
1，设n阶矩阵A=(aij) 的特征值为λ1 ,λ2 ,...λn ，则
a，λ1+ λ2 + ... + λn =a11 + a22 + … + ann
即：矩阵A的主对角线的元素的和 = 特征值的和
于是乎A的主对角线一定是十分重要的，那么我们就给它一个称呼吧，于是我们把矩阵A主行列式的元素和，称作矩阵A的迹。
b，λ1λ2… λn =|A|
即：特征值的乘积 = A的行列式
2，已知λ是方针A的特征值，则
a，λ2是A2的特征值
b，A可逆时，λ-1是A-1的特征值
3，如果A0= I，则λk是Ak的特征值，k∈R。
4，设λ1 ,λ2 ,...,λm 是方阵A的m个特征值，p1 ,p2,...,pm 是依次与之对应的特征向量，若λ1 ,λ2 ,...,λm 各不相等，则p1 ,p2 ,...,pm 线性无关。
即：不同特征值对应的特征向量线性无关。
5，实对称阵不同特征值的特征向量正交
6，对称矩阵A的特征向量是x，则xTAx是一个对角阵。
PS：如果A不是对称阵，则x-1Ax是对角阵。
最终结论：
设A为n阶对称阵，则必有正交阵P，使得
P-1AP= PTAP = Λ
Λ是以A的n个特征值为对角元的对角阵。
该变换称为“合同变换”，A和Λ互为合同矩阵。
以上是关于“正交阵”与“特征值和特征向量”的主要内容，如果未能解决你的问题，请参考以下文章