QR分解

Posted 2022-06-11 血影雪梦

         本总结是是个人为防止遗忘而作，不得转载和商用。

         关于如何求一个矩阵A的特征向量X和特征值λ，在上学时我们通常使用如下方法：

                      AX =λX =λIX （I：单位阵）

                  => |A -λI| = 0

                  => 求出λ

                   =>代入AX =λX求出X

         但在实际应用中这样没啥实际价值，实践中一般使用Q·R分解。

QR分解

         对于m×n的列满秩矩阵A，必有：

                   A_m*n= Q_m*n·R_n*n

         其中，Q^T·Q=I(即Q为正交矩阵)，R为非奇异上三角矩阵(即矩阵R的对角线下面的元素全为0)。

         这个将A分解成这样的矩阵Q和R的过程就是QR分解。

         其中当要求R的对角线元素为正时，该分解唯一。

         QR分解可用于求解矩阵A的特征值、A的逆等问题。

 

QR分解求特征值的过程：

         根据定义：A_m*n= Q_m*n·R_n*n，下面我们对该式做如下变换：

                    A = QR

                  => Q^TA = Q^TQR= R

                   =>Q^TAQ = RQ

         因为Q是正交阵，所以Q^TAQ的特征值不发生变化，所以想办法求出RQ的特征值就OK了。

         现在我们令A₁= RQ，然后对A₁做QR分解，得出A₁ = Q₂R₂，然后同上令A₂= R₂Q₂，就向这样一直进行下去最后求出An时，An就是一个“只有对角线上有值其他都为0的矩阵”，即：求出A的特征值了。

         文字描述就是上面了，用数学表述其过程就是：

                   A= QR  =>  A₁ = Q^TAQ  => RQ

                   ...

                   A_k= Q_kR_k  =>  A_k+1 = R_kQ_k

                   ...

                   A_k-> diagλ₁,λ₂, ...λ_n

 

         PS：

                   1，一般实践中不会直接做QR分解，因为下面的代码中那么一个简单的矩阵都经过了十几次迭代才收敛。实践中往往先把一个矩阵A通过HouseHolder变换做成上Hessenberg矩阵，然后通过Givens变换做QR分解。

                   2，和QR分解的还有Schmidt正交化，感兴趣的可以去查查。

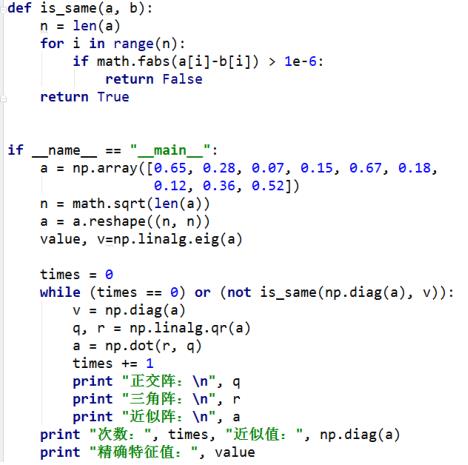
代码

         代码源自皱博老师，我就直接截图了：

                  

                    开发者涨薪指南 48位大咖的思考法则、工作方式、逻辑体系