纯万字干货机器学习之数据均衡算法种类大全+Python代码一文详解

Posted fanstuck

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了纯万字干货机器学习之数据均衡算法种类大全+Python代码一文详解相关的知识，希望对你有一定的参考价值。

前言

对于整个数据建模来看，数据均衡算法属于数据预处理一环。当整个数据集从调出数据库到拿到手的时候，对于分类数据集来说类别一般都是不均衡的，整个数据集合也是较为离散的。因此不可能一拿到数据集就可进行建模，类别的不均衡会极大影响建模判断准确率。其中我们希望整个数据集合的类别数目都是相似的，这样其特征数据权重能够更好的计算出来，便于分类。对于预测模型也是如此。数据均衡是整个数学建模以及研究最重要不得不重视的一环，下面我将详细介绍数据均衡的方法以及运用的不同场景。

一、为什么要做数据均衡？

首先在进行实验之前我们要了解数据均衡的重要性，这是一件值得我们去投入众多精力的事。一旦数据均衡做的不好将极大可能影响模型的准确性。数据预处理决定我们模型的上限，在一些重要的数学建模比赛或者是SCI论文中，数据均衡绝对是浓墨重彩的一环。我们可以这样思考：

        我们现在需要对一种疾病进行甄别，该病的发病概率为2%，而且很严重，100个人之间就可能会有2个人携带病毒。现在我们需要根据该病的特征数据构建能够判断患病的人。如果我们不进行数据均衡，倘若我们获得了10000份人的检测指标数据，其中有200人被标记为患病。那么我们立刻进行建模，因为患病人群数量极少，那么模型根据每一次特征权重计算反复迭代，获取最优的结果。那该模型为何不直接把判断人员数据归为健康人群呢。这样一来不管是判断的人群是否有无此病都能够得到98%的正确率甚至更高。那么我们的模型意义何在？

        若是根据这个模型，再给10份数据其中有5份是患病者数据，那么此时建立的模型丝毫没有用处，甚至造成严重的后果。所以说数据均衡是整个建模中很重要的一环。如果我们一开始就把这200份患病者的指标进行数据填充与健康数据均衡，那样我们还能够发现获得该病之后的指标显著特征，为后续医生的判断提供有力的支持。因此数据均衡是必不可少的一环，现在让我们来了解根据数据集场景的不同我们该如何进行数据均衡。

二、数据场景

1.大数据分布不均衡

拿两个我所遇到过的场景建模来说，第一个网络用户购买行为数据集来说。共拥有

十三万行的数据中仅3千条用户购买行为数据 ，这样大数据量的不均衡情况就为大数据量不均衡。

2.小数据分布不均衡

大数据量的不均衡情况居多，但难免有一些指标很难测量的场景。就如医学疾病检测。

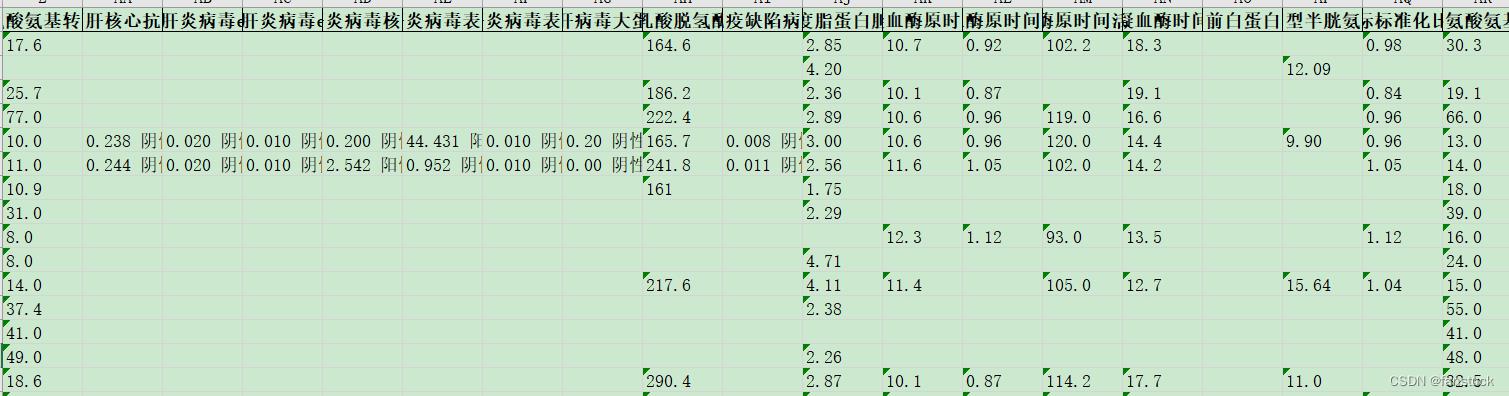
 该数据量小，仅有一万数据量，患病人数仅只有百名。这样的数据情况就为小数据分布不均衡。

这两类数据不均衡情况都有适合它们的处理算法。

三、均衡算法类型

在机器学习和深度学习中两者含义不同，但是思想方法类似。一个为数据中的采样方法，一个为图片的缩小和放大。这里重点解释机器学习的采样类型。

1.过采样

过采样也被称为上采样，这个方法更适用于小数据分布不均衡。如果是大数据分布不均衡，则将原来的小份类别不同的数据集扩充到与类别不同的数据集对等大小的情况。如第一个例子的数据，若进行过采样，则将会有超过26万的数据生成。与欠采样相比计算权重比例以及运算时间都会大大增加。甚至可能造成过拟合现象。而小数据分布不均衡运用该方法还能避免数据量太少引起的欠拟合。

以下是过采样效果图，图一为原始数据集。

 2.欠采样

欠采样也被称为下采样，一般将将较大的类别数据进行缩减，直至和类型不同的小量数据集相对等。如我们将例子一的数据进行欠采样，13w的用户行为数据将缩减至6730条数据，进行建模的速度将会大大的加快。

以下是欠采样算法效果图：

 

3.组合采样

不论是过采样和欠采样都会与原数据集存在一定的误差，过采样会导致很多样本的数据特征与原样本数据重叠导致难以分类清楚。而数据清洗技术恰好可以处理掉重叠样本，所以可以将二者结合起来形成一个组合采样，先过采样再进行数据清洗。

 

 

   四、算法具体种类

以Imbalancd sklearn库收录的算法来看，过采样共有11种方法，欠采样共有8种方法，组合采样有2种方法。

资源下载：机器学习之数据均衡算法种类大全+Python代码一文详解

 

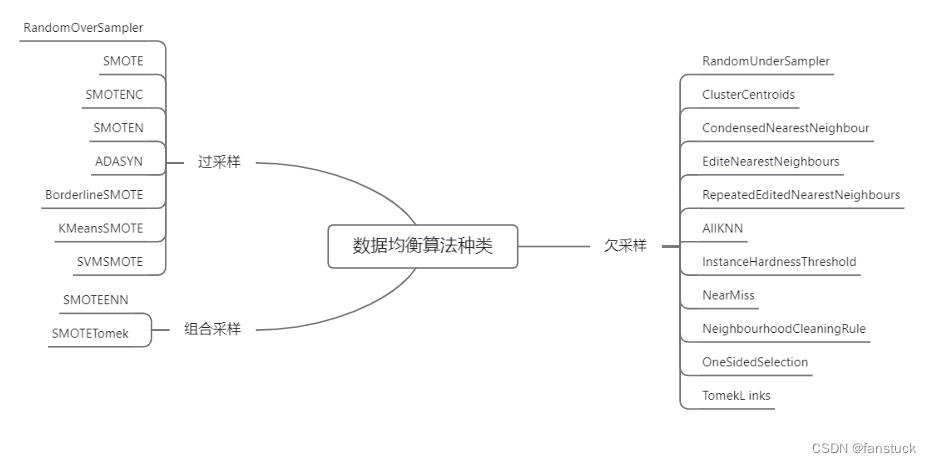
下面我们将从过采样-欠采样-组合采样大体三个类型的算法逐个了解其重算法种类的大致功能作用，以及使用场景：

1.欠采样算法：

 （1）.RandomUnderSampler

随机欠采样是十分快捷的方式，从多数类样本中随机选取一些剔除掉。但是随着采样方法的研究和发展随机欠采样已经很少使用。随机欠采样会损失大量的数据，可能被剔除的样本可能包含着一些重要信息，导致后续建模模型质量并不是很好。

from imblearn.under_sampling import RandomUnderSampler

X, y = create_dataset(n_samples=400, weights=(0.05, 0.15, 0.8), class_sep=0.8)

samplers = 
    FunctionSampler(),  # identity resampler
    RandomUnderSampler(random_state=0),


fig, axs = plt.subplots(nrows=2, ncols=2, figsize=(15, 15))
for ax, sampler in zip(axs, samplers):
    model = make_pipeline(sampler, clf).fit(X, y)
    plot_decision_function(
        X, y, model, ax[0], title=f"Decision function with sampler.__class__.__name__"
    )
    plot_resampling(X, y, sampler, ax[1])

fig.tight_layout()

（2）.ClusterCentroids

        通过使用K-Means聚类质心代替一个多数类的聚类，从而对多数类进行欠采样。通过带有N个聚类的KMeans算法拟合到多数类，并以N个聚类质心的坐标作为新的多数样本，从而保留N个多数样本。这和K-means方法原理是一样的

import matplotlib.pyplot as plt
from imblearn import FunctionSampler
from imblearn.pipeline import make_pipeline
from imblearn.under_sampling import ClusterCentroids

X, y = create_dataset(n_samples=400, weights=(0.05, 0.15, 0.8), class_sep=0.8)

samplers = 
    FunctionSampler(),  # identity resampler
    ClusterCentroids(random_state=0),


fig, axs = plt.subplots(nrows=2, ncols=2, figsize=(15, 15))
for ax, sampler in zip(axs, samplers):
    model = make_pipeline(sampler, clf).fit(X, y)
    plot_decision_function(
        X, y, model, ax[0], title=f"Decision function with sampler.__class__.__name__"
    )
    plot_resampling(X, y, sampler, ax[1])

fig.tight_layout()

：

 （3）.CondensedNearestNeighbour

CondensedNearestNeighbour 使用1近邻的方法来进行迭代, 来判断一个样本是应该保留还是剔除, 具体的实现步骤如下:

  1. 集合C: 所有的少数类样本;
  2. 选择一个多数类样本(需要下采样)加入集合C, 其他的这类样本放入集合S;
  3. 使用集合S训练一个1-NN的分类器, 对集合S中的样本进行分类;
  4. 将集合S中错分的样本加入集合C;
  5. 重复上述过程, 直到没有样本再加入到集合C.
     
from imblearn.under_sampling import (
    CondensedNearestNeighbour,
    OneSidedSelection,
    NeighbourhoodCleaningRule,
)

X, y = create_dataset(n_samples=500, weights=(0.2, 0.3, 0.5), class_sep=0.8)

fig, axs = plt.subplots(nrows=3, ncols=2, figsize=(15, 25))

samplers = [
    CondensedNearestNeighbour(random_state=0),
    OneSidedSelection(random_state=0),
    NeighbourhoodCleaningRule(),
]

for ax, sampler in zip(axs, samplers):
    model = make_pipeline(sampler, clf).fit(X, y)
    plot_decision_function(
        X, y, clf, ax[0], title=f"Decision function for \\nsampler.__class__.__name__"
    )
    plot_resampling(
        X, y, sampler, ax[1], title=f"Resampling using \\nsampler.__class__.__name__"
    )
fig.tight_layout()

 （4）.EditedNearestNeighbours

（5）.RepeatedEditedNearestNeighbours

 EditedNearestNeighbours删除其类别与其最近邻之一不同的多数类别的样本。这就是原理 RepeatedEditedNearestNeighbours。 通过更改内部最近邻算法的参数，在每次迭代中增加它，与AllKNN略有不同 。

from imblearn.under_sampling import (
    EditedNearestNeighbours,
    RepeatedEditedNearestNeighbours,
    AllKNN,
)

X, y = create_dataset(n_samples=500, weights=(0.2, 0.3, 0.5), class_sep=0.8)

samplers = [
    EditedNearestNeighbours(),
    RepeatedEditedNearestNeighbours(),
    AllKNN(allow_minority=True),
]

fig, axs = plt.subplots(3, 2, figsize=(15, 25))
for ax, sampler in zip(axs, samplers):
    model = make_pipeline(sampler, clf).fit(X, y)
    plot_decision_function(
        X, y, clf, ax[0], title=f"Decision function for \\nsampler.__class__.__name__"
    )
    plot_resampling(
        X, y, sampler, ax[1], title=f"Resampling using \\nsampler.__class__.__name__"
    )

fig.tight_layout()

 （6）.AllKNN

 与RepeatedEditedNearestNeighbours不同的是，该算法内部的最近邻算法的近邻数在每次迭代中都会增加。

代码在上面统一概括了，此三类算法类似，只不过都以EditedNearestNeighbours为基础在此上进行优化：

 （7）.InstanceHardnessThreshold

InstanceHardnessThreshold使用分类器的预测来排除样本。所有以低概率分类的样本都将被删除。

from imblearn.under_sampling import InstanceHardnessThreshold

samplers = 
    FunctionSampler(),  # identity resampler
    InstanceHardnessThreshold(
        estimator=LogisticRegression(),
        random_state=0,
    ),


fig, axs = plt.subplots(nrows=2, ncols=2, figsize=(15, 15))
for ax, sampler in zip(axs, samplers):
    model = make_pipeline(sampler, clf).fit(X, y)
    plot_decision_function(
        X,
        y,
        model,
        ax[0],
        title=f"Decision function with \\nsampler.__class__.__name__",
    )
    plot_resampling(
        X, y, sampler, ax[1], title=f"Resampling using \\nsampler.__class__.__name__"
    )

fig.tight_layout()
plt.show()

 （8）.NearMiss

NearMiss算法实施一些启发式规则以选择样本。NearMiss-1 从多数类中选择最近的少数类样本的平均距离最小的样本。NearMiss-2 从多数类中选择与负类最远样本的平均距离最小的样本。NearMiss-3 是一个两步算法：首先，对于每个少数样本， 将保留其最近邻；然后，选择的大多数样本是与最近邻居的平均距离最大的样本。

from imblearn.under_sampling import NearMiss

X, y = create_dataset(n_samples=1000, weights=(0.05, 0.15, 0.8), class_sep=1.5)

samplers = [NearMiss(version=1), NearMiss(version=2), NearMiss(version=3)]

fig, axs = plt.subplots(nrows=3, ncols=2, figsize=(15, 25))
for ax, sampler in zip(axs, samplers):
    model = make_pipeline(sampler, clf).fit(X, y)
    plot_decision_function(
        X,
        y,
        model,
        ax[0],
        title=f"Decision function for sampler.__class__.__name__-sampler.version",
    )
    plot_resampling(
        X,
        y,
        sampler,
        ax[1],
        title=f"Resampling using sampler.__class__.__name__-sampler.version",
    )
fig.tight_layout()

 

 （9）.NeighbourhoodCleaningRule

  NeighbourhoodCleaningRule使用 EditedNearestNeighbours删除一些样本。此外，他们使用 3 个最近邻删除不符合此规则的样本。

代码已贴在CondensedNearestNeighbour那一栏：

 （10）OneSidedSelection

使用了 1-NN 并用于TomekLinks删除被认为有噪声的样本。

代码已贴在CondensedNearestNeighbour那一栏：

（11）. TomekLinks

TomekLinks :样本x与样本y来自于不同的类别,满足以下条件,它们之间被称之为TomekLinks:不存在另外一个样本z,使得d(x,z) < d(x.y)或者d(y,z) < d(x,y)成立.其中d(.)表示两个样本之间的距离,也就是说两个样本之间互为近邻关系.这个时候,样本x或样本y很有可能是噪声数据,或者两个样本在边界的位置附近。
TomekL inks函数中的auto参数控制Tomek' s links中的哪些样本被剔除.默认的ratio= 'auto'’ 移除多 数类的样本,当ratio='ll'时,两个样本均被移除.

from collections import Counter
from sklearn.datasets import make_classification
from imblearn.under_sampling import TomekLinks 
X, y = make_classification(n_classes=2, class_sep=2,
weights=[0.1, 0.9], n_informative=3, n_redundant=1, flip_y=0,
n_features=20, n_clusters_per_class=1, n_samples=1000, random_state=10)
tl = TomekLinks()
X_res, y_res = tl.fit_resample(X, y)

2.过采样算法：

在随机过采样的基础上，通过样本构造一方面降低了直接复制样本代理的过拟合的风险，另一方法实现了样本的均衡。比如样本构造方法 SMOTE（Synthetic minority over-sampling technique）及其衍生算法。

（1）.SMOTE

通过从少量样本集合中筛选的样本 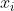 和 及对应的随机数 ，通过两个样本间的关系来构造新的样本 。SMOTE算法的基本思想是对少数类样本进行分析并根据少数类样本人工合成新样本添加到数据集中，具体如下图所示，算法流程如下：

  1. 对于少数类中每一个样本 ，以欧氏距离为标准计算它到少数类样本集中所有样本的距离，得到其 k 近邻。
  2. 根据样本不平衡比例设置一个采样比例以确定采样倍率N，对于每一个少数类样本 ，从其k近邻中随机选择若干个样本，假设选择的近邻为 。
  3. 对于每一个随机选出的近邻 ，分别与原样本 按照如下的公式构建新的样本。

 

伪代码：

 

SMOTE会随机选取少数类样本用以合成新样本，而不考虑周边样本的情况，这样容易带来两个问题：

  1. 如果选取的少数类样本周围也都是少数类样本，则新合成的样本不会提供太多有用信息。这就像支持向量机中远离margin的点对决策边界影响不大。
  2. 如果选取的少数类样本周围都是多数类样本，这类的样本可能是噪音，则新合成的样本会与周围的多数类样本产生大部分重叠，致使分类困难。

总的来说我们希望新合成的少数类样本能处于两个类别的边界附近，这样往往能提供足够的信息用以分类。

from imblearn import FunctionSampler  # to use a idendity sampler
from imblearn.over_sampling import SMOTE, ADASYN

X, y = create_dataset(n_samples=150, weights=(0.1, 0.2, 0.7))

fig, axs = plt.subplots(nrows=2, ncols=2, figsize=(15, 15))

samplers = [
    FunctionSampler(),
    RandomOverSampler(random_state=0),
    SMOTE(random_state=0),
    ADASYN(random_state=0),
]

for ax, sampler in zip(axs.ravel(), samplers):
    title = "Original dataset" if isinstance(sampler, FunctionSampler) else None
    plot_resampling(X, y, sampler, ax, title=title)
fig.tight_layout(

 

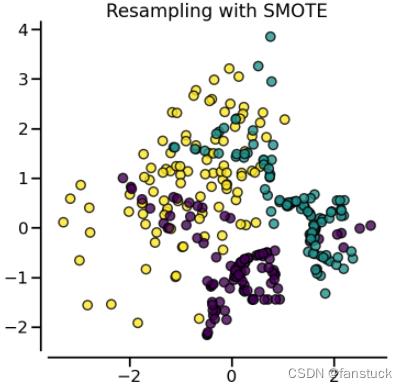
 （2）.RandomOverSampler

从样本少的类别中随机抽样，再将抽样得来的样本添加到数据集中。然而这种方法如今已经不大使用了，因为重复采样往往会导致严重的过拟合，因而现在的主流过采样方法是通过某种方式人工合成一些少数类样本，从而达到类别平衡的目的。

from imblearn.pipeline import make_pipeline
from imblearn.over_sampling import RandomOverSampler

X, y = create_dataset(n_samples=100, weights=(0.05, 0.25, 0.7))

fig, axs = plt.subplots(nrows=1, ncols=2, figsize=(15, 7))

clf.fit(X, y)
plot_decision_function(X, y, clf, axs[0], title="Without resampling")

sampler = RandomOverSampler(random_state=0)
model = make_pipeline(sampler, clf).fit(X, y)
plot_decision_function(X, y, model, axs[1], f"Using model[0].__class__.__name__")

fig.suptitle(f"Decision function of clf.__class__.__name__")
fig.tight_layout()

 （3）SMOTEN、BorderlineSMOTE、KMeansSMOTE、SVMSMOTE

SMOTE 通过识别在重采样期间要考虑的特定样本来提出几种变体。边界版本 ( BorderlineSMOTE) 将检测在两个类之间的边界中选择哪个点。SVM 版本 ( SVMSMOTE) 将使用使用 SVM 算法找到的支持向量来创建新样本，而 KMeans 版本 ( KMeansSMOTE) 将在之前进行聚类，根据每个集群密度在每个集群中独立生成样本。

from imblearn.over_sampling import BorderlineSMOTE, KMeansSMOTE, SVMSMOTE

X, y = create_dataset(n_samples=5000, weights=(0.01, 0.05, 0.94), class_sep=0.8)

fig, axs = plt.subplots(5, 2, figsize=(15, 30))

samplers = [
    SMOTE(random_state=0),
    BorderlineSMOTE(random_state=0, kind="borderline-1"),
    BorderlineSMOTE(random_state=0, kind="borderline-2"),
    KMeansSMOTE(random_state=0),
    SVMSMOTE(random_state=0),
]

for ax, sampler in zip(axs, samplers):
    model = make_pipeline(sampler, clf).fit(X, y)
    plot_decision_function(
        X, y, clf, ax[0], title=f"Decision function for sampler.__class__.__name__"
    )
    plot_resampling(X, y, sampler, ax[1])

fig.suptitle("Decision function and resampling using SMOTE variants")
fig.tight_layout()

 

在处理连续和分类特征的混合时， SMOTENC是唯一可以处理这种情况的方法。

from collections import Counter
from imblearn.over_sampling import SMOTENC

rng = np.random.RandomState(42)
n_samples = 50
# Create a dataset of a mix of numerical and categorical data
X = np.empty((n_samples, 3), dtype=object)
X[:, 0] = rng.choice(["A", "B", "C"], size=n_samples).astype(object)
X[:, 1] = rng.randn(n_samples)
X[:, 2] = rng.randint(3, size=n_samples)
y = np.array([0] * 20 + [1] * 30)

print("The original imbalanced dataset")
print(sorted(Counter(y).items()))
print()
print("The first and last columns are containing categorical features:")
print(X[:5])
print()

smote_nc = SMOTENC(categorical_features=[0, 2], random_state=0)
X_resampled, y_resampled = smote_nc.fit_resample(X, y)
print("Dataset after resampling:")
print(sorted(Counter(y_resampled).items()))
print()
print("SMOTE-NC will generate categories for the categorical features:")
print(X_resampled[-5:])
print()

但是，如果数据集仅由分类特征组成，则应使用SMOTEN.：

from imblearn.over_sampling import SMOTEN

# Generate only categorical data
X = np.array(["A"] * 10 + ["B"] * 20 + ["C"] * 30, dtype=object).reshape(-1, 1)
y = np.array([0] * 20 + [1] * 40, dtype=np.int32)

print(f"Original class counts: Counter(y)")
print()
print(X[:5])
print()

sampler = SMOTEN(random_state=0)
X_res, y_res = sampler.fit_resample(X, y)
print(f"Class counts after resampling Counter(y_res)")
print()
print(X_res[-5:])
print()

 （4）.ADASYN

 不平衡学习的自适应综合采样方法，

 ADASYN思想：基于根据少数类数据样本的分布自适应地生成少数类数据样本的思想:与那些更容易学习的少数类样本相比，更难学习的少数类样本会生成更多的合成数据。ADASYN方法不仅可以减少原始不平衡数据分布带来的学习偏差，还可以自适应地将决策边界转移到难以学习的样本上。关键思想是使用密度分布作为标准来自动决定需要为每个少数类样本生成的合成样本的数量。从物理上来说，是根据不同少数族的学习难度来衡量他们的权重分布。ADASYN后得到的数据集不仅将提供数据分布的平衡表示(根据β系数定义的期望平衡水平)，还将迫使学习算法关注那些难以学习的样本。
 

from imblearn import FunctionSampler  # to use a idendity sampler
from imblearn.over_sampling import SMOTE, ADASYN

X, y = create_dataset(n_samples=150, weights=(0.1, 0.2, 0.7))

fig, axs = plt.subplots(nrows=2, ncols=2, figsize=(15, 15))

samplers = [
    FunctionSampler(),
    RandomOverSampler(random_state=0),
    SMOTE(random_state=0),
    ADASYN(random_state=0),
]

for ax, sampler in zip(axs.ravel(), samplers):
    title = "Original dataset" if isinstance(sampler, FunctionSampler) else None
    plot_resampling(X, y, sampler, ax, title=title)
fig.tight_layout()

 3.组合采样

 （1）.SMOTETomek、SMOTEENN

 SMOTE允许生成样本。但是，这种过采样方法对底层分布没有任何了解。因此，可能会生成一些噪声样本，例如，当不同的类别不能很好地分离时。因此，应用欠采样算法来清理噪声样本可能是有益的。文献中通常使用两种方法：（i）Tomek 的链接和（ii）编辑最近邻清理方法。不平衡学习提供了两个即用型采样器SMOTETomek和 SMOTEENN. 

 

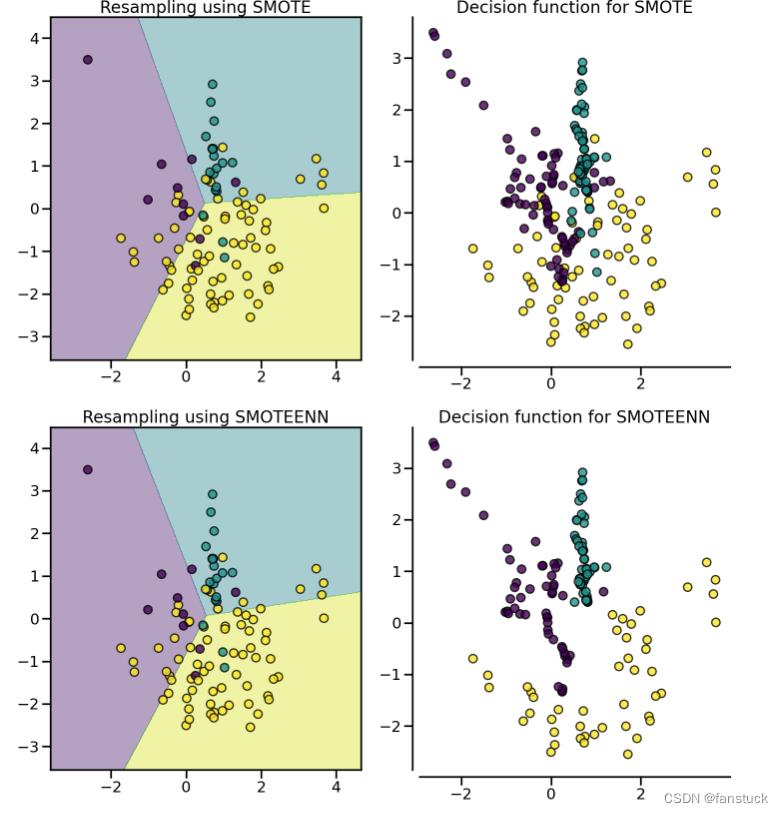
关于每个采样方法的参数和具体细致的原理将会在我的机器学习专栏逐个讲到：机器学习

该方法是建立在：数据预处理 之后开展的，若想要从建模0开始十分推荐订阅我个人博客~

点关注，防走丢，如有纰漏之处，请留言指教，非常感谢

以上就是本期全部内容。我是fanstuck ，有问题大家随时留言讨论 ，我们下期见。

 

开发者涨薪指南 48位大咖的思考法则、工作方式、逻辑体系

以上是关于纯万字干货机器学习之数据均衡算法种类大全+Python代码一文详解的主要内容，如果未能解决你的问题，请参考以下文章

[Python从零到壹] 十三.机器学习之聚类算法四万字总结全网首发（K-MeansBIRCH树状聚类MeanShift）

机器学习之样本不均衡

机器学习之集成学习

机器学习之决策树与随机森林模型

[Python从零到壹] 十二.机器学习之回归分析万字总结全网首发（线性回归多项式回归逻辑回归）

强烈推荐机器学习之算法篇