LeetCode 54.螺旋矩阵 - 原地修改

Posted 2022-05-31 Tisfy

【LetMeFly】54.螺旋矩阵 - 原地修改

力扣题目链接：https://leetcode.cn/problems/spiral-matrix/

给你一个 m行 n列的矩阵 matrix，请按照 顺时针螺旋顺序 ，返回矩阵中的所有元素。

示例 1:

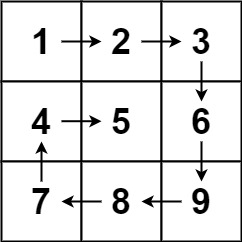
输入：matrix = [[1,2,3],[4,5,6],[7,8,9]]
输出：[1,2,3,6,9,8,7,4,5]

示例 2:

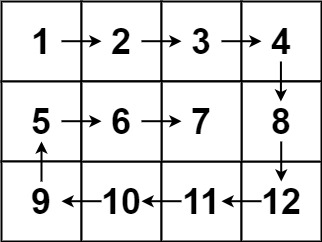
输入：matrix = [[1,2,3,4],[5,6,7,8],[9,10,11,12]]
输出：[1,2,3,4,8,12,11,10,9,5,6,7]

提示:

• $m==matrix.length$
• $n==matrix[i].length$
• $1<=m,n<=10$
• $-100\le matrix[i][j]\le 100$

思路

我们只需要从$(0,0)$开始，按题目意思模拟即可。

方法一：模拟（简单，但需要修改原数组）

先小开心一波，这次执行效率小高了一次嘻嘻

我们定义一个directions数组，来代表要遍历的方向。

const int directions[4][2] = 0, 1, 1, 0, 0, -1, -1, 0;  // 分别对应：👉👇👈👆

然后还需要一个变量nowDirection，来记录当前的方向。

用变量loc来记录当前已经遍历过的元素的数量，当已遍历的数量小于总元素个数时，继续遍历。

int loc = 0;  // 遍历了几个元素了
while (loc < n) 
    继续遍历

每次遍历时，先把当前位置的元素存入答案中（用$x$和$y$记录当前位置，初始值都为$0$），标记当前位置为已遍历过并把$loc+1$。

因为题目中说元素的数据范围是$[-100,100]$，所以我们可以把已遍历过的元素标记为$101$

ans[loc++] = matrix[x][y];
matrix[x][y] = ALREADY;  // ALREADY的值可以是101

然后就看下一个位置是否未被遍历过

#define ifOK(x, y) if (x >= 0 && x < matrix.size() && y >= 0 && y < matrix[0].size() && matrix[x][y] != ALREADY)  // 判断(x, y)是否OK（既在数据范围内又没被遍历过）
int nx = x + directions[nowDirection][0];
int ny = y + directions[nowDirection][1];
ifOK(nx, ny) 
    ...

如果下一个元素可行就更新$x$和$y$为当前方向的下一个元素；

如果下一个元素不可行就更改遍历方向为下一个方向，并更新$x$和$y$为新方向的下一个元素。

nowDirection = (nowDirection + 1) % 4;
x += directions[nowDirection][0];
y += directions[nowDirection][1];

• 时间复杂度$O(nm)$
• 空间复杂度$O(1)$，但是注意如果不允许修改原数组，则此方法将要消耗O(nm)的空间复杂度。

AC代码

C++

#define ALREADY 101
#define ifOK(x, y) if (x >= 0 && x < matrix.size() && y >= 0 && y < matrix[0].size() && matrix[x][y] != ALREADY)
const int directions[4][2] = 0, 1, 1, 0, 0, -1, -1, 0;  // 👉👇👈👆

class Solution 
public:
    vector<int> spiralOrder(vector<vector<int>>& matrix) 
        int n = matrix.size() * matrix[0].size();
        vector<int> ans(n);
        int nowDirection = 0;  // 现在的方向
        int loc = 0;  // 遍历了几个元素了
        int x = 0, y = 0;  // 当前应该遍历的位置
        while (loc < n) 
            ans[loc++] = matrix[x][y];
            matrix[x][y] = ALREADY;
            int nx = x + directions[nowDirection][0];
            int ny = y + directions[nowDirection][1];
            ifOK(nx, ny) 
                x = nx, y = ny;
            
            else 
                nowDirection = (nowDirection + 1) % 4;
                x += directions[nowDirection][0];
                y += directions[nowDirection][1];
            
        
        return ans;
    
;

方法二：模拟（不那么好想，但不需要修改原数组）

方法一中，我们判断前进方向是否修改的方式是“看下一个点有没有走过”。因此我们把已经走过的点做了个标记。

那么，有没有什么 不看下一个点是否走过就能判断是否该转向了 的办法呢？答案当然是有的。

接下来让我们来绘制一下走向图：

以5*6的表格为例，生成html表格的Emmet代码为（在支持Emmet语法的编辑器中输入下面代码按回车即可）：

center>table[style="border: 0px solid #0094ff; border-collapse: collapse; padding: 1px; table-layout: fixed; text-align: center;"]>tr[style="border: 1px solid #0094ff; height: 70px"]*5>td[style="border: 1px solid #0094ff; width: 70px"]*6

然后填入要前进的方向：

👉	👉	👉	👉	👉	⤵️
⮫	👉	👉	👉	⤵️	👇
👆	⮫	👉	⤵️	👇	👇
👆	↖	👈	👈	↲	👇
↖	👈	👈	👈	👈	↲

图片版本为：

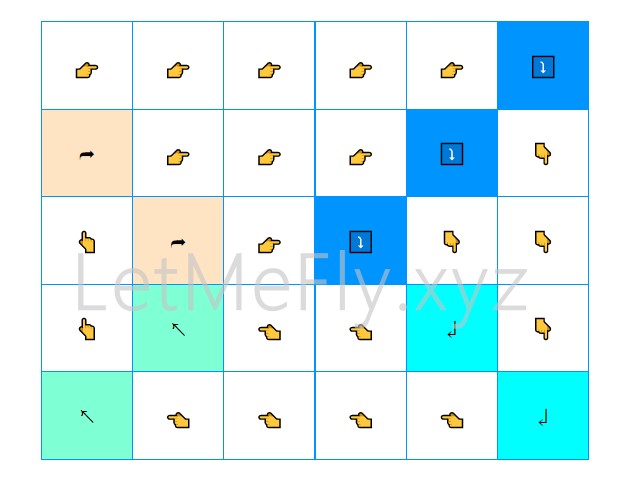
不难发现，若以下标为$0$开始：

• 需要右转下的位置都在一条负对角线上，且这些点满足$x+y=列数-1$。因此，当前进方向为向右且遍历到的位置坐标满足$x+y=列数-1$时，应当调整遍历方向为向下。
• 同理，下转左的条件为$x-y=行数-列数$
• 左转上的条件为$x+y=行数-1$
• 上转右的条件为$x-y=1$

这样我们就不修改原始数组，就能判断什么时候该改变方向了。

• 时间复杂度$O(nm)$
• 空间复杂度$O(1)$，因为根本不需要修改原数组

AC代码

C++

const int directions[4][2] = 0, 1, 1, 0, 0, -1, -1, 0;  // 👉👇👈👆

class Solution 
public:
    vector<int> spiralOrder(vector<vector<int>>& matrix) 
        int rows = matrix.size(), cols = matrix[0].size();  // 行数，列数
        vector<int> ans(rows * cols);
        int nowDirection = 0;
        int loc = 0;
        int x = 0, y = 0;
        while (loc < rows * cols) 
            ans[loc++] = matrix[x][y];
            if (nowDirection == 0 && x + y == cols - 1)   // 右转下
                nowDirection = 1;
            
            else if (nowDirection == 1 && x - y == rows - cols)   // 下转左
                nowDirection = 2;
            
            else if (nowDirection == 2 && x + y == rows - 1)   // 左转上
                nowDirection = 3;
            
            else if (nowDirection == 3 && x - y == 1)   // 上转右
                nowDirection = 0;
            
            x += directions[nowDirection][0];
            y += directions[nowDirection][1];
            // // DebugBegin
            // printf("x = %d, y = %d, nowDirection = %d\\n", x, y, nowDirection);
            // if (!(x >= 0 && x < rows && y >= 0 && y < cols)) 
            //     printf("Error!\\n");
            //     break;
            // 
            // // DebugEnd
        
        return ans;
    
;

这是我较为用心写的一篇博客，题解图片是由HTML画的。同步发文于CSDN，原创不易，转载请附上原文链接哦~
Tisfy：https://letmefly.blog.csdn.net/article/details/125016209