独孤九剑第一式-岭回归和Lasso回归

Posted 2022-05-25 吃猫的鱼python

🍌文章适合于所有的相关人士进行学习🍌
🍋各位看官看完了之后不要立刻转身呀🍋
🍑期待三连关注小小博主加收藏🍑
🍉小小博主回关快 会给你意想不到的惊喜呀🍉

---

文章目录

• • 🐲前言
  • 🐲岭回归
  • • • 🐮岭回归的引出
      • 🐮岭回归的系数推导
      • 🐮岭回归代码部分
  • 🐲Lasso回归模型
  • • • 🐮Lasso代码部分

🐲前言

从今天开始我就要传授给大家独孤九剑秘籍了，今天是第一🗡。
我们今天讲解的是机器学习中的岭回归和Lasso回归模型，这两种相对来讲比较简单一点，也比较容易理解，希望大家跟住。

🐲岭回归

🐮岭回归的引出

我们上次学习了关于多重线性回归模型的相关知识，并对其理论进行了数学推导，我们今天还是从这里入手，相关复习知识请回顾多重线性回归模型，根据线性回归的参数回归公式我们最后推导的结果是

这里就有一个问题就是，在实际应用的过程当中，可能出现以下两种情况：

1. 出现自变量个数多余样本量个数，（矩阵中列数多于行数）。举个例子，根据我们学习过的线性代数
   
   此时就不存在逆矩阵。
2. 自变量之间存在严重的多重共线性，自变量之间存在强相关。
   

很明显，我们可以发现第一列和第三列是2倍的关系，根据线性代数的相关知识我们也可以知道其对应的逆矩阵和它相乘是为0的，那么如果是0的话我们就无法判断参数的最小值了，那么我们怎么办呢？
这里科学家们就提出了加入一个l2正则项来进行约束，也称之为惩罚项。

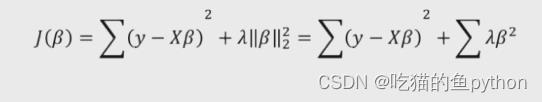
在线性回归模型的目标函数之上添加l2正则项，其中ᵰ 为非负数
当ᵰ =0时，目标函数退化为线性回归模型的目标函数
当ᵰ →+∞时，通过缩减回归系数使ᵯ 趋近于0
当趋近于正无穷的时候，那么目标函数也趋近于正无穷，我们通过降低回归系数，来制约目标函数趋近这无穷这种趋势，最后得到相对应的系数求解。

🐮岭回归的系数推导

这里我们就求出了参数的最终结果。然后我们的公式还可以进行凸优化，对于数学专业的同学应该了解的多一点，可以转化为：

然后我们根据这两个公式画图。

锥形对应公式前面部分，圆柱对应后面部分。对应到平面之上就更加可以体现出这种关系。当其相交的点就是参数对应的点。此时求得函数最小。或者如果没有相交的点，那么距离最近的点就是所求的对应参数。
那么我们如何确定拉姆达参数呢？这里我们举一个例子来讲述：
现在有100条数据，分为毫无关联（无重叠的十组），我们先定义参数拉姆达为1，挑选第一组来验证模型的好坏，然后剩余9组用来建模。然后再挑选第二组，剩余9组继续建模，然后挑选第三组。。。一直到所有都结束，找出所有的中最优的一组。
然后我们再取参数拉姆达为2，继续这个流程，然后再取3。重复

这里就是代码的说明，其中scoring就是检测模型好坏的依据方法，我们这里使用MSE的方法，也就是均方误差验证。

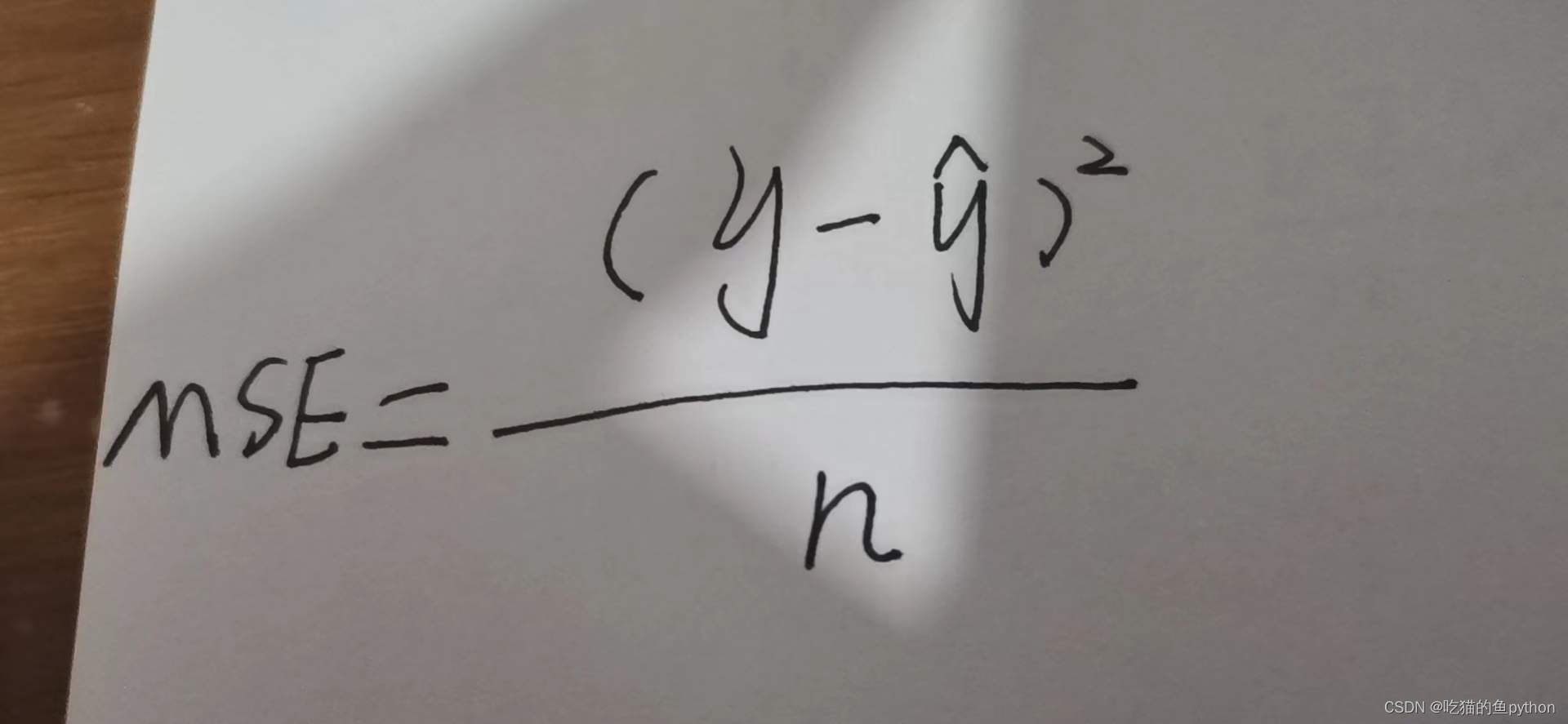
这里对应的预测值y当然就是越接近y值就越好了，所以MSE越小对应的结果就越好。

🐮岭回归代码部分

数据部分

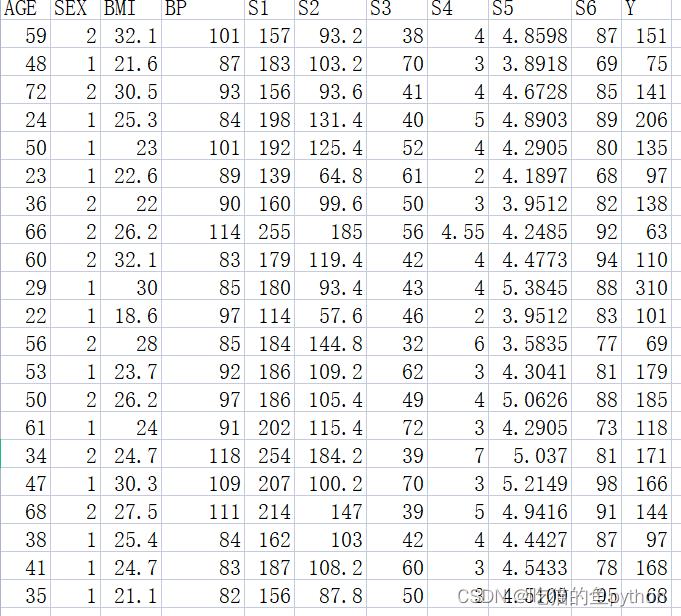
导入库

import pandas as pd
import numpy as np
from sklearn import model_selection 
from sklearn.linear_model import Ridge,RidgeCV#线性回归模型的岭回归
import matplotlib.pyplot as plt

分为训练集和测试集

diabetes = pd.read_excel(r'diabetes.xlsx', sep = '')
# 构造自变量（剔除患者性别、年龄和因变量）只取第三列到最后一列但是取不到最后一列
predictors = diabetes.columns[2:-1]
# 将数据集拆分为训练集和测试集
X_train, X_test, y_train, y_test = model_selection.train_test_split(diabetes[predictors], diabetes['Y'], 
                                                                    test_size = 0.2, random_state = 1234 )#分为自变量和因变量

十重交叉验证

Lambdas = np.logspace(-5, 2, 200)#-5到2呈现等比数列 生成200个数值
# 岭回归模型的交叉验证
# 设置交叉验证的参数，对于每一个Lambda值，都执行10重交叉验证
ridge_cv = RidgeCV(alphas = Lambdas, normalize=True, scoring='neg_mean_squared_error', cv = 10)#十重交叉验证，数值为Lambda
# 模型拟合   CV指的是 cross v
ridge_cv.fit(X_train, y_train)#对之前的进行拟合
# 返回最佳的lambda值
ridge_best_Lambda = ridge_cv.alpha_
ridge_best_Lambda

最后的结果是0.0135…
这里我们就求出了最优的值。

岭回归参数检测和均方误差检测

from sklearn.metrics import mean_squared_error
# 基于最佳的Lambda值建模
ridge = Ridge(alpha = ridge_best_Lambda, normalize=True)
ridge.fit(X_train, y_train)
# 返回岭回归系数
pd.Series(index = ['Intercept'] + X_train.columns.tolist(),data = [ridge.intercept_] + ridge.coef_.tolist())
# 预测
ridge_predict = ridge.predict(X_test)
# 预测效果验证
RMSE = np.sqrt(mean_squared_error(y_test,ridge_predict))
RMSE

结果是53

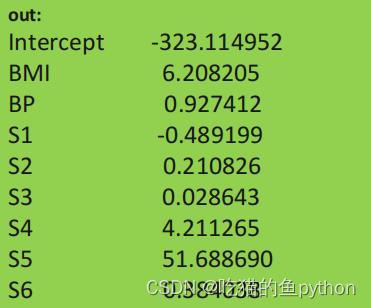
🐲Lasso回归模型

其实Lasso回归模型和岭回归很像很像，就是把惩罚项进行了变化，但是这种变化最终的结果就是，继续优化了岭回归，可以完成降维，由三维降为二维。
科学家们引入了l1正则项，也称之为惩罚项。

凸优化的等价命题是

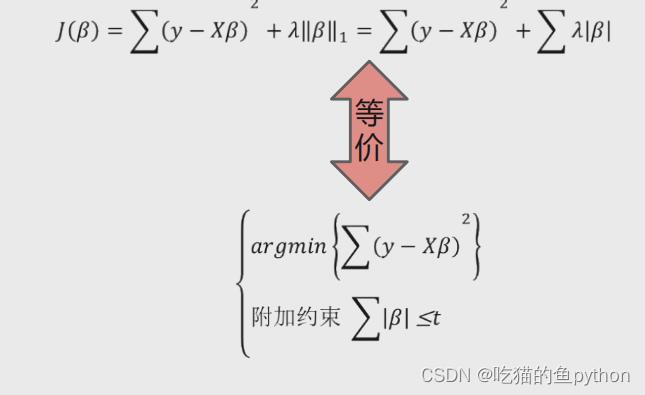
进行画图后：

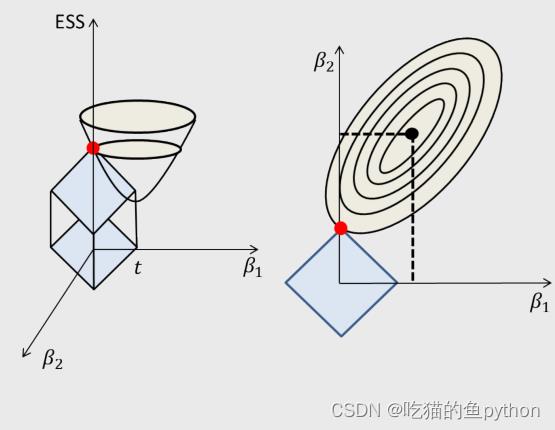
也正是由于它由平方项变为了绝对值项，模型优圆形变为了方形。增添了很多的‘角’，也就是棱角部分，所以与椭圆相接的部分就很有可能再坐标轴上，所以可以完成降维。

这里我们解释一下tol。
max_iter表示迭代1000次则退出本次求解参数，tol表示误差，如果误差和实际值小于0.0001，则退出求解本次参数。两者哦都是对最后求解参数的一种结束条件。

🐮Lasso代码部分

from sklearn.linear_model import Lasso,LassoCV
# LASSO回归模型的交叉验证
lasso_cv = LassoCV(alphas = Lambdas, normalize=True, cv = 10, max_iter=10000)
lasso_cv.fit(X_train, y_train)
# 输出最佳的lambda值
lasso_best_alpha = lasso_cv.alpha_
lasso_best_alpha

然后进行Lasso模型拟合

lasso = Lasso(alpha = lasso_best_alpha, normalize=True, max_iter=10000)
lasso.fit(X_train, y_train)
# 返回LASSO回归的系数
pd.Series(index = ['Intercept'] + X_train.columns.tolist(),data = [lasso.intercept_] + lasso.coef_.tolist())

# 预测
lasso_predict = lasso.predict(X_test)
# 预测效果验证
RMSE = np.sqrt(mean_squared_error(y_test,lasso_predict))
RMSE

结果为53.06

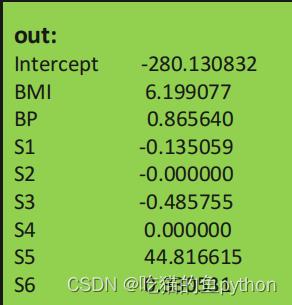
这里就可以明显的看到了S2和S4都变成了0，降了2维。
今天我们的讲解到这里就结束了！！！

🍌文章适合于所有的相关人士进行学习🍌
🍋各位看官看完了之后不要立刻转身呀🍋
🍑期待三连关注小小博主加收藏🍑
🍉小小博主回关快 会给你意想不到的惊喜呀🍉