正则化——参数范数惩罚
Posted Drawing1998
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了正则化——参数范数惩罚相关的知识,希望对你有一定的参考价值。
正则化——参数范数惩罚
正则化的定义:“对学习算法的修改——旨在减少泛化误差而不是训练误差。”
直观理解:正则化就是用来减少模型过拟合的一种策略。
接下来介绍的是正则化最常见的方法之一——对模型的权重进行
L
1
L^1
L1 和
L
2
L^2
L2 正则化。
所谓的
L
1
L^1
L1 和
L
2
L^2
L2 正则化,其实就是利用了
L
1
L^1
L1 和
L
2
L^2
L2 范数,来规范模型参数(权重
w
w
w)的一种方法。
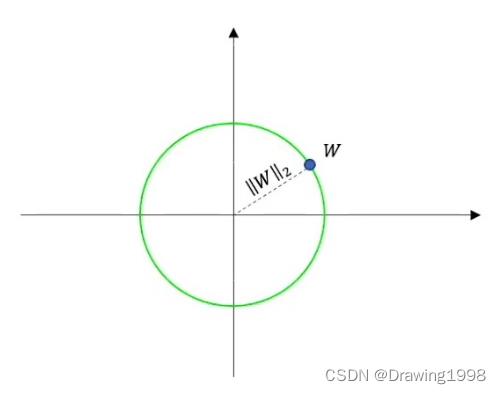
范数,我们可以理解为就是对空间中两点的距离这个概念进行了扩充。例如权重 w w w,它是一个高维向量,也可以理解为是空间中的一个点,它到原点的距离,如果是曼哈顿距离的话就是 L 1 L^1 L1 范数,如果是欧氏距离的话就是 L 2 L^2 L2 范数。
- L 0 L^0 L0 范数:向量中非零元素的个数。
- L 1 L^1 L1 范数: ∣ ∣ W ∣ ∣ 1 = ∣ w 1 ∣ + ∣ w 2 ∣ + . . . + ∣ w i ∣ ||W||_1 = |w_1| + |w_2| + ... + |w_i| ∣∣W∣∣1=∣w1∣+∣w2∣+...+∣wi∣ (曼哈顿距离)
- L 2 L^2 L2 范数: ∣ ∣ W ∣ ∣ 2 = ∣ w 1 ∣ 2 + ∣ w 2 ∣ 2 + . . . + ∣ w i ∣ 2 ||W||_2 = \\sqrt|w_1|^2 + |w_2|^2 + ... + |w_i|^2 ∣∣W∣∣2=∣w1∣2+∣w2∣2+...+∣wi∣2 (欧氏距离)
由于真正带来过拟合问题的是权重
w
w
w,为了简单起见,在下面的讨论中,我们只重点考虑
w
w
w。
1. L2 参数正则化
L 2 L^2 L2 参数正则化通常被称为权重衰减,它通过向目标函数添加一个 正则项 Ω ( θ ) = 1 2 ∣ ∣ w ∣ ∣ 2 2 \\Omega(\\theta) = \\frac12||\\pmbw||^2_2 Ω(θ)=21∣∣www∣∣22 ,使权重更加接近原点。
那么问题来了: L 2 L^2 L2 参数正则化为什么被称为权重衰减呢?他是怎么使权重得到衰减的呢?
损失函数: J ( w , b ) J(\\pmbw, b) J(www,b)
权重更新: w = w − ϵ ⋅ ▽ w J ( w ) \\pmbw = \\pmbw -\\epsilon\\cdot\\bigtriangledown_wJ(\\pmbw) www=www−ϵ⋅▽wJ(www)
对于损失函数 J ( W , b ) J(W, b) J(W,b) ,我们想要找到一组参数 ( w ∗ , b ∗ ) (\\pmbw^*, b^*) (www∗,b∗) 来 minimize J ( w , b ) J(\\pmbw, b) J(www,b) 。
为了简单起见,我们只考虑权重
w
w
w,这样模型的目标函数就是:
J
~
(
w
;
X
,
y
)
=
α
2
w
T
w
+
J
(
w
;
X
,
y
)
\\widetildeJ(\\pmbw; \\pmbX, \\pmby) = \\frac\\alpha2w^Tw + J(\\pmbw; \\pmbX, \\pmby)
J
(www;XXX,yyy)=2αwTw+J(www;XXX,yyy)其中,
α
∈
[
0
,
∞
)
\\alpha \\in [0, \\infty)
α∈[0,∞) 被称为衰减率,是权衡范数惩罚项
Ω
\\Omega
Ω 和 标准目标函数
J
J
J 相对贡献的超参数。将
α
\\alpha
α 设置为0表示没有正则化;
α
\\alpha
α 越大,对应正则化惩罚越大。在求解过程中,我们通过缩放惩罚项
Ω
\\Omega
Ω 的超参数
α
\\alpha
α 来控制
L
2
L^2
L2以上是关于正则化——参数范数惩罚的主要内容,如果未能解决你的问题,请参考以下文章