蚁群算法详解及其工程源码

Posted 2022-05-18 IT技术猿猴

目录

蚁群算法定义

蚁群算法原理

蚁群算法基本流程

matlab源码：

---

蚁群算法定义

        蚁群算法(ant colony optimization, ACO)，又称蚂蚁算法，是一种用来在图中寻找优化路径的机率型算法。它由Marco Dorigo于1992年在他的博士论文中提出，其灵感来源于蚂蚁在寻找食物过程中发现路径的行为。蚁群算法是一种模拟进化算法，初步的研究表明该算法具有许多优良的性质。针对PID控制器参数优化设计问题，将蚁群算法设计的结果与遗传算法设计的结果进行了比较，数值仿真结果表明，蚁群算法具有一种新的模拟进化优化方法的有效性和应用价值。

---

蚁群算法是一种本质上并行的算法。每只蚂蚁搜索的过程彼此独立，仅通过信息激素进行通信，它在问题空间的多点同时进行独立搜索，不仅增加了算法的可靠性，也使得算法具有较强的全局搜索能力。

蚁群算法是对自然界蚂蚁的寻径方式进行模拟而得出的一种仿生算法。蚂蚁在运动过程中会留下信息素，蚂蚁在运动时又可以感知这种物质，来确定自己的运动方向。因此，大量蚂蚁组成的蚂蚁群体的集体行为表现出一种信息的正反馈现象。

---

蚁群算法的思想来源于自然界蚂蚁觅食，蚂蚁在寻找食物源时，会在路径上留下蚂蚁独有的路径标识——信息素，蚂蚁会感知其他蚂蚁在各条路径上留下的信息素，并根据各条路径上的信息素浓度来选择之后要走的路，路径上留有的信息浓度越高，则蚂蚁更倾向于选择该路径。在蚂蚁选择某条路径后也会在改路径上留下信息素吸引更多蚂蚁选择该路径，随着时间的推移，信息素浓度不断增大，蚂蚁选择路径的概率也随之增高，由此形成了正反馈机制。由于蚁群算法的正反馈性，因此蚁群算法也属于增强型学习算法的其中一种。

---

蚁群算法原理

初始时刻，不妨将P kij (t)设为t时刻蚂蚁k从结点i转移到结点j的概率。“蚂蚁TSP”策略收到两方面的左右，首先是访问某结点的概率，这个概率的大小依赖于其他蚂蚁释放的信息素浓度。所以定义：

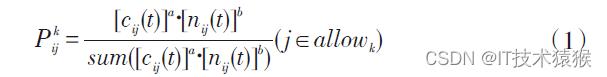
式中，nkij (t)为启发函数，表示蚂蚁从结点i转移到结点j的概率；allowk为蚂蚁k下一步可转移结点的集合，随着时间的推移，allowk储存的元素数量会减小，最终会变为空集合。a 为信息素重要程度因子。

与实际情况类似的一点是：随着时间的推移，残留在路径上的信息素会逐渐挥发，蚂蚁在经过路径时残留的信息素量也会逐渐等同于信息素挥发量，最终使信息素残留量趋于稳定。令α表示信息素挥发程度，那么所有蚂蚁遍历完所有结点之后，各路径上的信息素残留量的数学表达式如下：

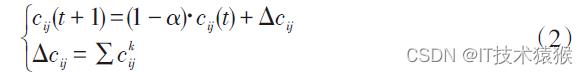
式中，ckij为第k只蚂蚁在连接结点i 与结点k的路径上释放信息素而增加的信息素浓度。Δckij为所有蚂蚁在结点i 与结点k 连接路径上释放信息素而增加的信息素浓度，通常情况下：

式中，Q为路径信息素常量，I为第k 只蚂蚁所经过路径的总长度[3]。

蚂蚁回退策略

蚂蚁在搜索路径时，以当前节点为中心，来选择目标路径上的下一个节点，在搜索复杂环境中会有不连通路径，此刻蚂蚁无路可行，即落入陷阱，由于蚂蚁落入陷阱而不能自救，就会处于死亡状态，算法会出现停滞现象。这说明算法健壮性不够强，需要设计策略来避免蚂蚁陷入陷阱中。因此为了避免此类问题，加入蚂蚁回退策略来提高算法鲁棒性。改进的信息素更新。

在基本蚁群算法中，蚁群完成一次循环后信息素更新如下：

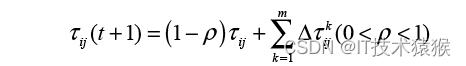
式中：P表示信息素挥发率，取值范围( 0,1) ；   k/ij表示在节点i到j路径上，第k只蚂蚁释放的信息素。为了避免传统蚁群算法陷入局部最优和提高收敛速度。研究表明，狼群捕获猎物后会把食物分给最强壮的狼吃，保证强壮狼群捕获更多的猎物来维持种群生存，而弱小的狼最终会被饿死而淘汰。加入狼群分配策略后，进行更新的信息素如下：

式中 ：Lb本次局部循环最短路径，Lg 是本次局部最差路径 ；b,w分别表示本次循环中局部最短、最差蚂蚁个数[4]。

改进的转移概率

蚁群算法中不可避免出现死锁蚂蚁，究其根本原因是由于蚂蚁在搜索路径时不可避免会遇到周围的节点都是己走过的或者存在障碍物的情形，蚂蚁不可通过，只能停留在原地。根据公式为此搜索初期采取避障策略，增加避障因子，为了提高算法效率，定义一个用于替代启发函数   ij 的目标吸引度函数。

式中： gjs 表示用DIJKSTRA 算法计算的节点j 到目标点g的最短距离。将式代如式，得到了蚂蚁改进后的转移概率为：

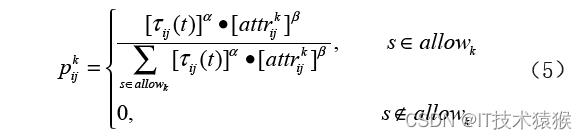
根据环境的建立可对蚂蚁在复杂野外环境下的路径搜索进行引导，提高了蚂蚁选择离目标点更邻近节点的概率。

---

蚁群算法基本流程

 

---

---

 C#工程源码：

点击这里获取基于C#的蚁群算法工程源码

---

matlab源码：

%% 旅行商问题(TSP)优化
%% 清空环境变量
clear all
clc

%% 导入数据
load citys_data.mat

%% 计算城市间相互距离
fprintf('Computing Distance Matrix... \\n');
n = size(citys,1);
D = zeros(n,n);
for i = 1:n
    for j = 1:n
        if i ~= j
            D(i,j) = sqrt(sum((citys(i,:) - citys(j,:)).^2));
        else
            D(i,j) = 1e-4;      
        end
    end    
end

%% 初始化参数
fprintf('Initializing Parameters... \\n');
m = 50;                              % 蚂蚁数量
alpha = 1;                           % 信息素重要程度因子
beta = 7;                            % 启发函数重要程度因子
rho = 0.1;                           % 信息素挥发因子
Q = 1;                               % 常系数
Eta = 1./D;                          % 启发函数
Tau = ones(n,n);                     % 信息素矩阵
Table = zeros(m,n);                  % 路径记录表
iter = 1;                            % 迭代次数初值
iter_max = 150;                      % 最大迭代次数 
Route_best = zeros(iter_max,n);      % 各代最佳路径       
Length_best = zeros(iter_max,1);     % 各代最佳路径的长度  
Length_ave = zeros(iter_max,1);      % 各代路径的平均长度  

%% 迭代寻找最佳路径
figure;
while iter <= iter_max
    fprintf('迭代第%d次\\n',iter);
    % 随机产生各个蚂蚁的起点城市
      start = zeros(m,1);
      for i = 1:m
          temp = randperm(n);
          start(i) = temp(1);
      end
      Table(:,1) = start; 
      % 构建解空间
      citys_index = 1:n;
      % 逐个蚂蚁路径选择
      for i = 1:m
          % 逐个城市路径选择
         for j = 2:n
             tabu = Table(i,1:(j - 1));           % 已访问的城市集合(禁忌表)
             allow_index = ~ismember(citys_index,tabu);
             allow = citys_index(allow_index);  % 待访问的城市集合
             P = allow;
             % 计算城市间转移概率
             for k = 1:length(allow)
                 P(k) = Tau(tabu(end),allow(k))^alpha * Eta(tabu(end),allow(k))^beta;
             end
             P = P/sum(P);
             % 轮盘赌法选择下一个访问城市
             Pc = cumsum(P);     
            target_index = find(Pc >= rand); 
            target = allow(target_index(1));
            Table(i,j) = target;
         end
      end
      % 计算各个蚂蚁的路径距离
      Length = zeros(m,1);
      for i = 1:m
          Route = Table(i,:);
          for j = 1:(n - 1)
              Length(i) = Length(i) + D(Route(j),Route(j + 1));
          end
          Length(i) = Length(i) + D(Route(n),Route(1));
      end
      % 计算最短路径距离及平均距离
      if iter == 1
          [min_Length,min_index] = min(Length);
          Length_best(iter) = min_Length;  
          Length_ave(iter) = mean(Length);
          Route_best(iter,:) = Table(min_index,:);
      else
          [min_Length,min_index] = min(Length);
          Length_best(iter) = min(Length_best(iter - 1),min_Length);
          Length_ave(iter) = mean(Length);
          if Length_best(iter) == min_Length
              Route_best(iter,:) = Table(min_index,:);
          else
              Route_best(iter,:) = Route_best((iter-1),:);
          end
      end
      % 更新信息素
      Delta_Tau = zeros(n,n);
      % 逐个蚂蚁计算
      for i = 1:m
          % 逐个城市计算
          for j = 1:(n - 1)
              Delta_Tau(Table(i,j),Table(i,j+1)) = Delta_Tau(Table(i,j),Table(i,j+1)) + Q/Length(i);
          end
          Delta_Tau(Table(i,n),Table(i,1)) = Delta_Tau(Table(i,n),Table(i,1)) + Q/Length(i);
      end
      Tau = (1-rho) * Tau + Delta_Tau;
    % 迭代次数加1，清空路径记录表

 %   figure;
 %最佳路径的迭代变化过程
    [Shortest_Length,index] = min(Length_best(1:iter));
    Shortest_Route = Route_best(index,:);
    plot([citys(Shortest_Route,1);citys(Shortest_Route(1),1)],...
    [citys(Shortest_Route,2);citys(Shortest_Route(1),2)],'o-');
    pause(0.3);
 
    iter = iter + 1;
    Table = zeros(m,n);

 % end
end

%% 结果显示
[Shortest_Length,index] = min(Length_best);
Shortest_Route = Route_best(index,:);
disp(['最短距离:' num2str(Shortest_Length)]);
disp(['最短路径:' num2str([Shortest_Route Shortest_Route(1)])]);

%% 绘图
figure(1)
plot([citys(Shortest_Route,1);citys(Shortest_Route(1),1)],...
     [citys(Shortest_Route,2);citys(Shortest_Route(1),2)],'o-');
grid on
for i = 1:size(citys,1)
    text(citys(i,1),citys(i,2),['   ' num2str(i)]);
end
text(citys(Shortest_Route(1),1),citys(Shortest_Route(1),2),'       起点');
text(citys(Shortest_Route(end),1),citys(Shortest_Route(end),2),'       终点');
xlabel('城市位置横坐标')
ylabel('城市位置纵坐标')
title(['蚁群算法优化路径(最短距离:' num2str(Shortest_Length) ')'])
figure(2)
plot(1:iter_max,Length_best,'b',1:iter_max,Length_ave,'r:')
legend('最短距离','平均距离')
xlabel('迭代次数')
ylabel('距离')
title('各代最短距离与平均距离对比')