实时音频编解码之十八 Opus解码 CELT解码

Posted 2022-05-18 shichaog

本文谢绝任何形式转载，谢谢。

5.3 CELT解码

Opus的CELT层使用窗长重叠为5ms~22.5ms的改进离散余弦变换 （Modified Discrete Cosine Transform，MDCT）算法，MDCT谱被按照人耳听觉灵敏度划分的Bark子带分解，通常CELT层有21个子带，在Hybird模式，前17个子带（到8kHz）由SILK层编解码，各频带包含的MDCT频点数量是不同的，最少就一个频点，最多176个频点，如表5-19所示。每个频带增益（能量）和频谱形状是分开编码的，这种独立编码频带增益方法使得保持信号谱包络变得简单，即使用PVQ编码没有增益信息的频谱包络形状。

帧长	2.5ms	5ms	10ms	20ms	起始频点	截止频点
频带	频点
0	1	2	4	8	0Hz	200Hz
1	1	2	4	8	200Hz	400Hz
2	1	2	4	8	400Hz	600Hz
…
20	22	44	88	176	15600Hz	20000Hz

表5-19 各帧长每个频带的MDCT频点数

对于基于变换方法的编码器而言，瞬态信息（Transients）是比较难编码的，对此，CELT使用两种不同的策略：

1.使用多个更小的MDCT而非一个大MDCT变换以及 2.动态时频分辨率调整。

为了提高周期性信号编码质量，CELT使用了预滤波和后滤波结合的方法，预滤波在编码端衰减信号谐波能量，后滤波在解码端在恢复谐波成分初始增益的同时将编码噪声谱按照谐波谱形状调整，这种噪声整形目的是减少人能感知到的编码噪声。

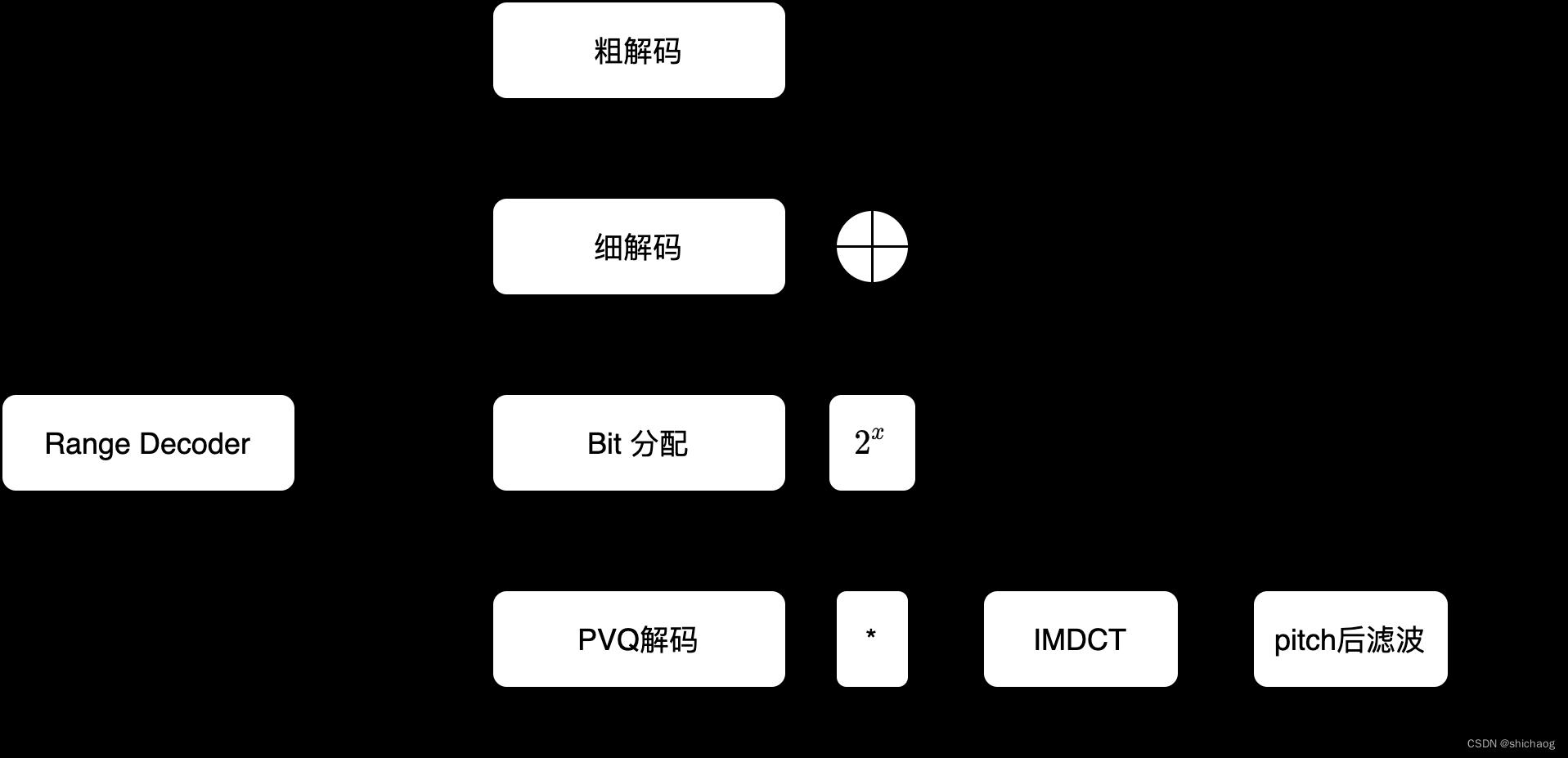
图5-6 CELT解码结构

图中IMDCT是Inverse MDCT的缩写，解码端接收到的编码比特流的内容如下表5-20所示：

符号	PDF	条件
silence	32767, 1/32768
后滤波	1, 1/2
octave	uniform (6)	后滤波
周期	raw bits (4+octave)	后滤波
增益	raw bits (3)	后滤波
tapset	2, 1, 1/4	后滤波
瞬态(transient)	7, 1/8
帧内(intra)	7, 1/8
coarse energy	5.3.2小节
tf_change	5.3.1小节
tf_select	1, 1/2	5.3.1小节
spread	7, 2, 21, 2/32
dyn. alloc.	5.3.3小节
alloc. trim
skip	1, 1/2	5.3.3小节
intensity	uniform	5.3.3小节
dual	1, 1/2
fine energy	5.3.2小节
residual	5.3.2小节
anti-collapse	1, 1/2	5.4.5小节
finalize	5.3.2小节

表5-20 编码比特率中CELT层编码符号存放顺序

解码端从区间编码器比特流中按照表5-20依次解码CELT层各符号值。

5.3.1 瞬态解码

瞬态标志该帧CELT层使用的是一个长的MDCT变换还是多个短的MDCT变换，当标志被置位后，则MDCT系数字段存放的是多个短MDCT变换的系数集，反之，则该字段是一个长的MDCT变换的系数。该标志编码到比特流中的概率是1/8，除了全局瞬态标志，每个频带还有自己的时频（time-frequency, tf）分辨率变化的二进制标志，时频分辨率变化定义于celt.c文件的tf_select_table[][]，只有当当帧长，瞬态标志以及tf_select值等条件满足时才会启用变化的时频分辨率。

5.3.2 谱包络解码

用足够的分辨率量化能量是很重要的，这是因为任何能量量化误差在后续的解码过程中无法补偿，无论用于编码各个频带的谱包络分辨率如何，保留每个频带能量在感知上都是非常重要的，CELT使用粗-细-细三步策略在底为2的对数域编码能量，其实现于quant_bands.c。

5.3.3 粗解码

能量的粗量化使用6dB这一固定分辨率，为最小化编码比特率，在时域（基于先前帧）和频域（基于先前频带）都进行预测滤波，可以通过创建一个不参考先前帧的“帧内”帧，对其能量编码时不参考先前的帧信息，进而不需要时域预测，解码器首先读取帧内（intra）标志以确定是否使用了帧内预测方式，预测滤波器的二维z变换如下式5-53所示：
$$A(z_l,z_b)=\frac{(1-\alpha z_l^{-1})\ast (1-z_b^{-1})}{1-\beta \ast z_b^{-1}}式5-53$$
其中b是频带索引，l是帧索引，当不使用“帧内”能量方式时预测系数依赖于帧长，当使用“帧内”能量方式时$\alpha =0,\beta =\frac{4915}{32768}$，时域预测基于前帧的最终细量化结果，而频域预测仅基于粗量化结果，为了使定点的实现和浮点实现具有一样的动态范围，在内部对预测值进行的截断操作。预测误差的理想分布使用帧内和帧间模式不同帧长参数的拉普拉斯分布逼近，这些参数见quant_bands.c的e_prob_model 表。粗能量的解码实现于unquant_coarse_energy() (quant_bands.c)，拉普拉斯分布值的解码使用 ec_laplace_decode() (laplace.c)。

5.3.4 能量细量化

每个频带的能量细量化比特位数取决于5.3.5小节比特分配计算方法，设$B_i$是频带i的能量细量化比特位数。则细量化是找取值在$[0,2^{B_i}-1]$的整数f，f和粗能量相关性的映射等价于$(f+1/2)/2^{B_i}-1/2$能量细量化实现于quant_fine_energy() (quant_bands.c)。

5.3.5 比特分配

CELT层每个频带的增益形状结构确保了每帧的各频带谱包络形状使用相同的比特编码，这使得频带的SNR近似常量，这使得编码噪声和信号谱包络具有相同的形状，心理声学上的掩蔽曲线同样符合信号谱包络形状，这意味着理想的分配在帧间更加一致。

许多编码器传输辅助信息以控制帧内比特分配，CELT层对每个频带有大量码本可供选择，因而可以适配很宽的比特率范围.

5.3.6 形状解码

每个频带的归一化谱包络使用PVQ编码的，最简单情况，5.3.5小节分配的比特位转为5.3.6.1小节的脉冲数量，在有了脉冲数量以及每个频带的采样点数信息之后，解码端根据5.3.6.2小节计算码本的大小，码本的大小用于解码码字索引（无符号整数值），该索引转为5.3.6.2小节的激励矢量，该实现归一化后使用。

5.3.6.1 比特位转为脉冲

虽然比特分配是以1/8比特位为单位的，量化需要脉冲数量为整数k，因而编码端查找最近接且不超过5.3.5小节分配的编码比特位的整数k，为了效率，查找的过程用查表的方式实现。

5.3.6.2 PVQ解码

PVQ的解码实现于decode_pulses() (cwrs.c)函数，解码的码字索引均匀分布于[0, V(N,K)-1]，V(N,K)是N个采样点K个脉冲的所有可能的组合，组合的总数可以使用递归的方式计算：
$$V(N,K)=V(N-1,K)+V(N,K-1)+V(N-1,K-1)，V(N,0)=1以及V(0,K)=0,K!=0式5-54$$
解码向量X的按下列过程恢复，令区间解码器的ft等于V(N,K)以及k = K，则对于取值从0到 (N - 1)范围的j使用如下处理：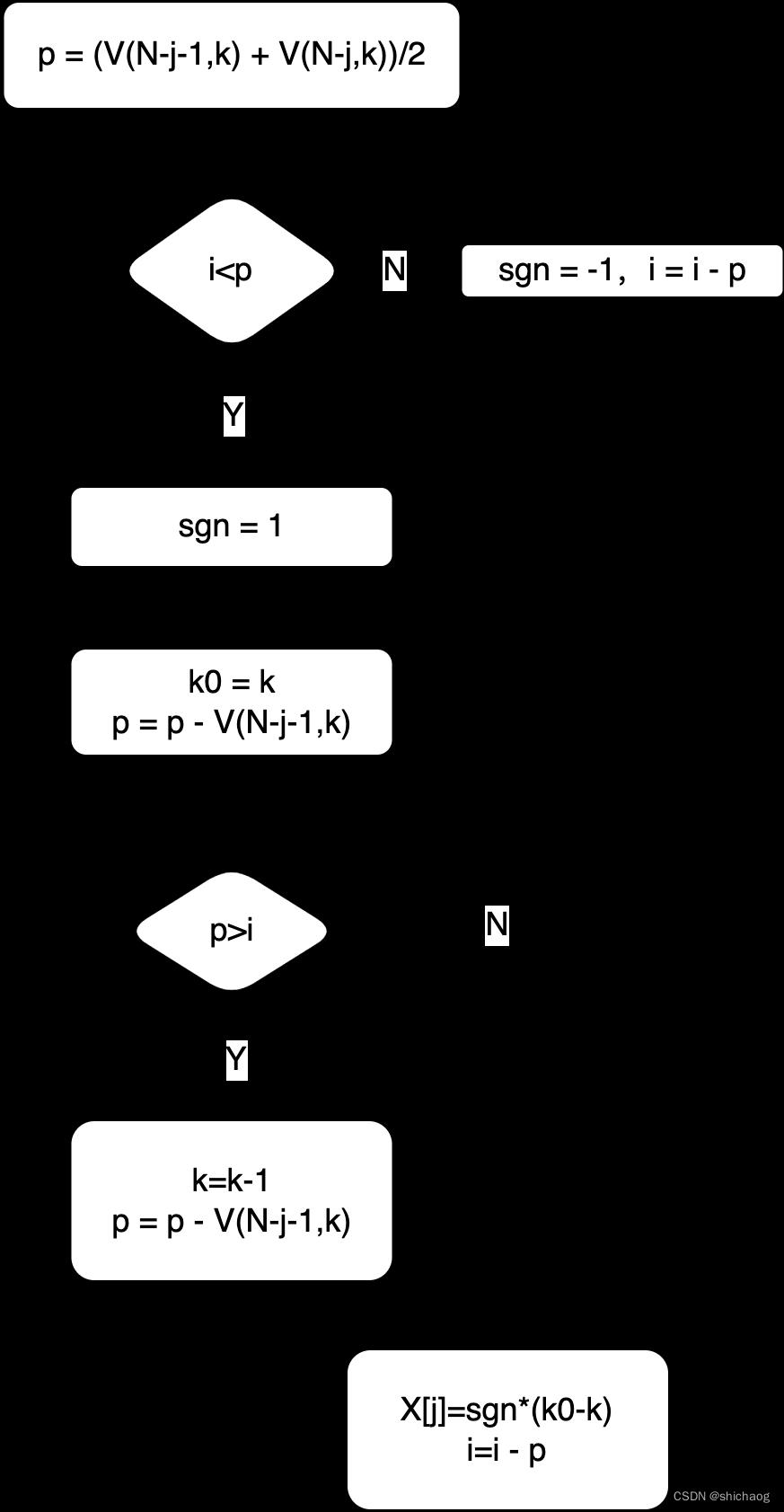

5.3.6.3 传播值

5.3.6.2小节解码的归一化矢量被旋转以便避免假的声调，旋转增益为g_r = N / (N + f_r*K)，N是维度，K是脉冲数，f_r是依赖于编码比特流中的“传播值”，旋转的角度为：
$$\theta =\frac{\pi \ast g_r^2}{4}式5-55$$
点$x_i$和$x_j$之间的二维旋转$R(i,j)$为：
$$x_i^{\prime }=\cos (\theta )\ast x_i+\sin (\theta )\ast x_j式5-56$$
$$x_j^{\prime }=-\sin (\theta )\ast x_i+\cos (\theta )\ast x_j式5-57$$
如果解码向量超过一个时间块，则传播操作需针对每个时间块都操作，如果每个块表示8个或更多点，则另一个角度为(pi/2-theta)的N为传播需要在上述的传播前进行，

5.3.6.4 分隔解码

为了避免PVQ矢量的多精度计算，码本允许的最大数量不超过32比特表示的范围，当需要更大的码本时，采用对半分隔编码矢量再分别编码的方法以约束码本数量，用熵编码的量化增益表示分隔每一侧的相对增益，并且这一表示递归应用于整个编码过程。多级拆分最多施加LM+1次。

5.3.6.5 时频变化

时频参数用于控制每个编码频带的时域分辨率和频域分辨率折中平衡，对于每个频带有两个时频分辨率备选项，对于第一个编码的频带，对于瞬态编码帧使用3, 1/4为编码PDF，其他类型的编码帧使用15, 1/16为PDF，对于后续的子带，对于瞬态帧用PDF15, 1/16，瞬态之外的使用31, 1/32 PDF相对先前的时频选择编码，负TF调整意味着时间分辨率增加，而正TF调整意味着频率分辨率增加。时频分辨率调整使用Hadamard 变换实现。

5.3.7 抗混叠处理

抗混叠是为了处理一些频带因使用多个小的MDCT而可能出现这些小的MDCT存在能量为零情况，当编码帧的瞬态（trainsient）置位时（因采用多个短时MDCT变换）会接着译码一个抗混叠比特位，如果抗混叠比特位被置位，则会阻止小的MDCT能量骤降为零，即对能量骤降频带的MDCT位置，采取插入一个和前两帧最小能量差不多的伪随机信号，然后再对信号重新规整化以保持能量的特性。

5.3.8 去规范化

正如编码端对每个频带归一化一样，解码端在逆MDCT之前的最后一步是对频带去规范化，即每一个解码的归一化频带和解码能量的均方根相乘，这一过程实现于denormalise_bands() （bands.c）。

5.3.9 IMDCT

逆MDCT的输入是N个频域采样点，输出是幅值缩为二分之一的2N个时域采样点，逆MDCT使用的窗长影响算法延迟，其窗源自于维特比编码器使用的240个采样点的加窗方法，IMDCT和加窗实现于mdct_backward (mdct.c)。
$$w(n)=(\sin (\frac{\pi }{2}\ast \sin (\frac{\pi }{2}\ast \frac{n+1/2}{L})){)}^2$$

5.3.9.1 后滤波

逆MDCT的结果在加权和重叠相加之后再经过后滤波输出，尽管后滤波处在解码的最后位置，后滤波参数确实先编码的，其在编码比特流中紧随静音标志，后滤波可以使能或者禁止，当使能时，倍频程（octave）解码为[0,6]区间均分分布的整数值。一旦获得octave之后，the fine pitch within the octave is decoded
using 4+octave raw bits. 基频周期最终为(16<<octave)+fine_pitch-1，因而基频周期的取值范围是[15, 1022]，接下来解码增益为G=3*(int_gain+1)/32，后滤波系数索引使用2, 1, 1/4 PDF解码，索引值等于0时，三个系数是g0 = 0.3066406250, g1 = 0.2170410156, g2 =0.1296386719，索引值等于1时，三个系数是g0 =0.4638671875, g1 = 0.2680664062, g2 = 0，索引值等于2时，三个系数是g0 = 0.7998046875, g1 = 0.1000976562, g2 = 0。后滤波的计算如下：
$$y(n)=x(n)+G\ast (g0\ast y(n-T)+g1\ast (y(n-T+以上是关于实时音频编解码之十八\; Opus解码\; CELT解码的主要内容，如果未能解决你的问题，请参考以下文章$$

实时音频编解码之十五 Opus编码-CELT编码

实时音频编解码之十五 Opus编码-CELT编码

实时音频编解码之十七 Opus解码 SILK解码

实时音频编解码之十七 Opus解码 SILK解码

实时音频编解码之十 CELT编码器

实时音频编解码之十六 Opus解码