DBN原理及实践-TensorFlow

Posted 2022-05-12 ljtyxl

转自Luozm's Blog

深度信念网络（Deep Belief Networks，DBN）是一种概率生成模型，是多个受限玻尔兹曼机（Restricted Boltzmann Machines，RBM）的堆叠，其中每个RBM层与其上下两层相连，且任意层内的单元不相互连接。除了第一层和最后一层之外，DBN的每一层都有两个作用：作为前一层的隐藏层，或者作为后一层的输入（可视层）。堆叠的RBM层上可以连接一个Softmax层来将整个DBN当做分类器使用，也可以简单的在无监督学习中用于无标签数据的聚类。DBN通常用于识别，聚类和生成图像、影像序列或者动作捕捉，由Geoff Hinton和他的学生在2006年首次提出。

 

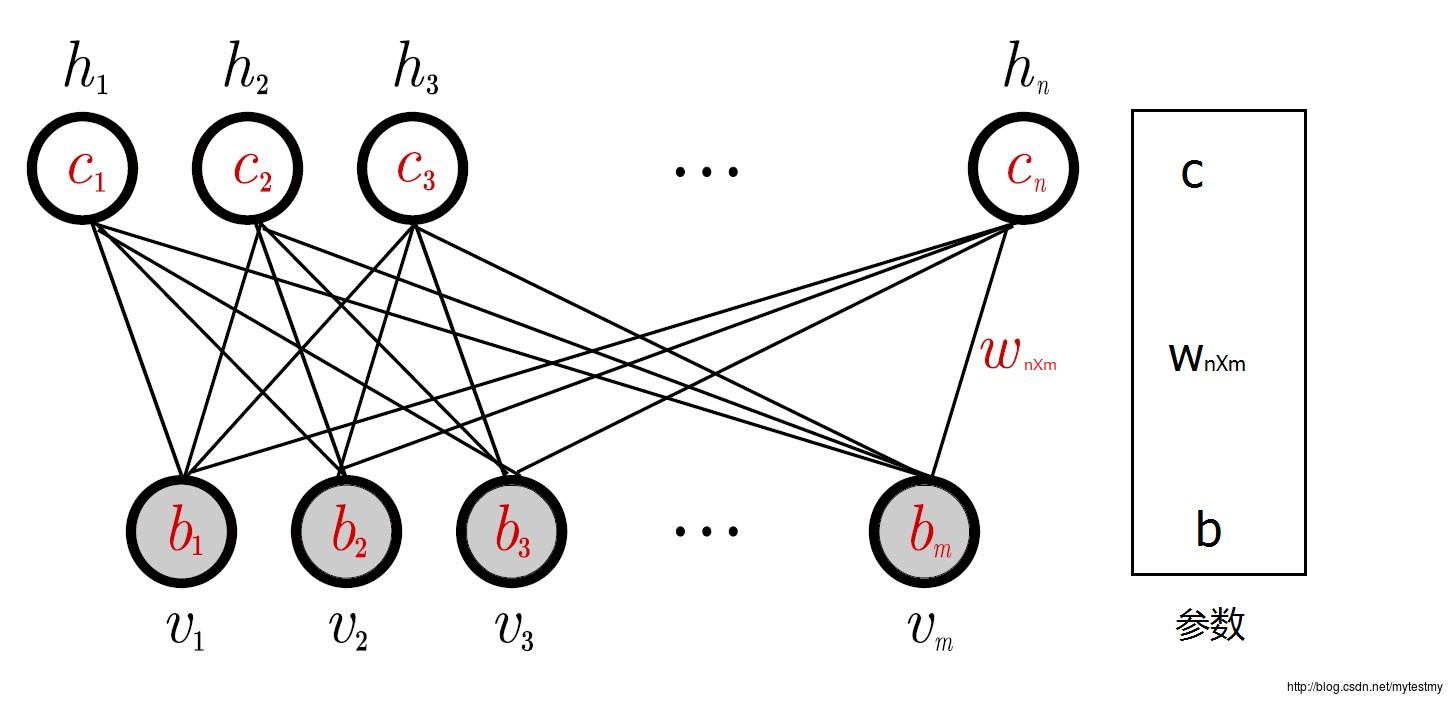
RBM网络有几个参数，一个是可视层与隐藏层之间的权重矩阵，一个是可视节点的偏移量b=(b1,b2⋯bm)，一个是隐藏节点的偏移量c=(c1,c2⋯cn)，这几个参数决定了RBM网络将一个m维的样本编码成一个什么样的n维的样本。

一个训练样本x过来了取值为x=(x1,x2⋯xm)，根据RBM网络，可以得到这个样本的m维的编码后的样本y=(y1,y2⋯yn)，这n维的编码也可以认为是抽取了n个特征的样本。而这个m维的编码后的样本是按照下面的规则生成的：对于给定的x=(x1,x2⋯xm)，隐藏层的第i个节点的取值为1（编码后的样本的第i个特征的取值为1）的概率为，其中的v取值就是x，hi的取值就是yi，其中，是sigmoid函数。也就是说，编码后的样本y的第i个位置的取值为1的概率是p(hi=1|v)。所以，生成yi的过程就是：
i）先利用公式，根据x的值计算概率p(hi=1|v)，其中vj的取值就是xj的值。
ii）然后产生一个0到1之间的随机数，如果它小于p(hi=1|v)，yi的取值就是1，否则就是0（假如p(hi=1|v)=0.6，这里就是因为yi的取值就是1的概率是,0.6，而这个随机数小于0.6的概率也是0.6；如果这个随机数小于0.6，就是这个事件发生了，那就可以认为yi的取值是1这个事件发生了，所以把yi取值为1）。
反过来，现在知道了一个编码后的样本y，想要知道原来的样本x，即解码过程，跟上面也是同理，过程如下：
i）先利用公式，根据y的值计算概率p(vj=1|h)，其中hi的取值就是yi的值。
ii）然后按照均匀分布产生一个0到1之间的随机浮点数，如果它小于p(vj=1|h)，vj的取值就是1，否则就是0。
 

RBM的用途：一是对数据进行编码，然后交给监督学习方法去进行分类或回归，二是得到了权重矩阵和偏移量，供BP神经网络初始化训练。三是可以计算联合分布，作为生成模型使用，四是可以计算条件概率，作为判别模型使用。

第一种可以说是把它当做一个降维的方法来使用。

第二种就用途比较奇怪。其中的原因就是神经网络也是要训练一个权重矩阵和偏移量，但是如果直接用BP神经网络，初始值选得不好的话，往往会陷入局部极小值。根据实际应用结果表明，直接把RBM训练得到的权重矩阵和偏移量作为BP神经网络初始值，得到的结果会非常地好。

第三种，RBM可以估计联合概率p(v,h)，如果把v当做训练样本，h当成类别标签（隐藏节点只有一个的情况，能得到一个隐藏节点取值为1的概率），就可以利用利用贝叶斯公式求p(h|v)，然后就可以进行分类，类似朴素贝叶斯、LDA、HMM。说得专业点，RBM可以作为一个生成模型（Generative model）使用。

第四种，RBM可以直接计算条件概率p(h|v)，如果把v当做训练样本，h当成类别标签（隐藏节点只有一个的情况，能得到一个隐藏节点取值为1的概率），RBM就可以用来进行分类。说得专业点，RBM可以作为一个判别模型（Discriminative model）使用。

一个样本和其对应编码的联合概率，也就是得到了RBM网络的Gibbs分布的概率密度函数，求解的目标也可以认为是让RBM网络表示的Gibbs分布与输入样本的分布尽可能地接近。求解输入样本的极大似然，就能让RBM网络表示的Gibbs分布和样本本身表示的分布最接近。 RBM问题最终可以转化为极大似然来求解。

LDA-math-MCMC 和 Gibbs Sampling

DBN原理及实践总结-1

DBN原理及实践总结-2

条件随机场（Conditional random field，CRF）

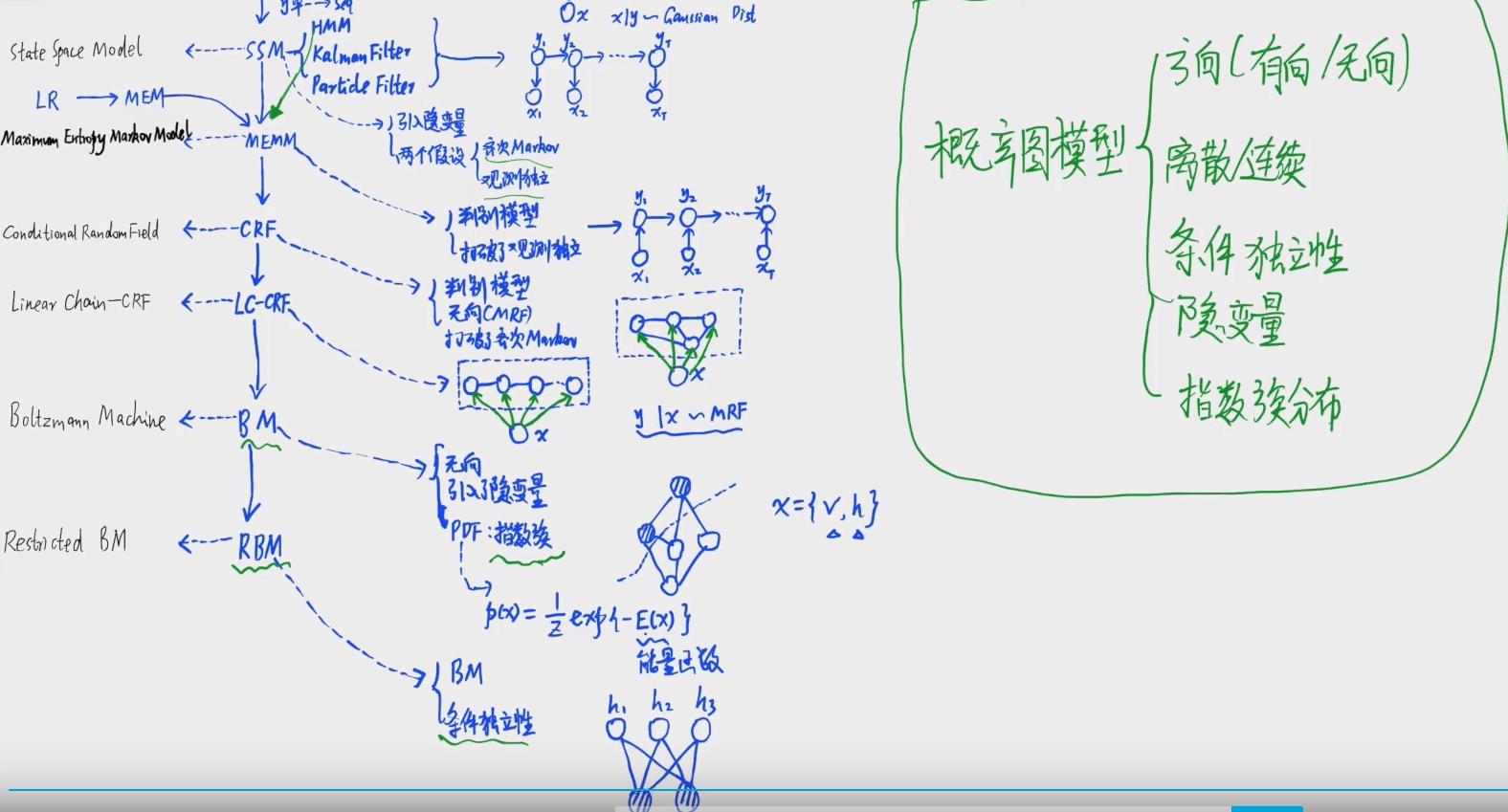
概率图模型（Probabilistic Graphical Model，PGM）使用一种基于图的表示来编码高维空间中的复杂联合概率分布。概率图模型的目的是提供一种机制能够利用复杂分布的结构来简洁地描述它们,并能有效地构造和利用它们。

一般PGM分为两类：Bayesian Network、Markov Random Field它们的主要区别在于采用不同类型的图来表达变量之间的关系：

贝叶斯网络采用有向无环图（Directed Acyclic Graph）来表达因果关系。一般来说，贝叶斯网络中每一个节点都对应于一个先验概率分布或者条件概率分布，因此整体的联合分布可以直接分解为所有单个节点所对应的分布的乘积。

马尔可夫随机场则采用无向图（Undirected Graph）来表达变量间的相互作用。对于马尔可夫场，由于变量之间没有明确的因果关系，它的联合概率分布通常会表达为一系列势函数（potential function）的乘积。通常情况下，这些乘积的积分并不等于1，因此，还要对其进行归一化才能形成一个有效的概率分布——这一点往往在实际应用中给参数估计造成非常大的困难。

 

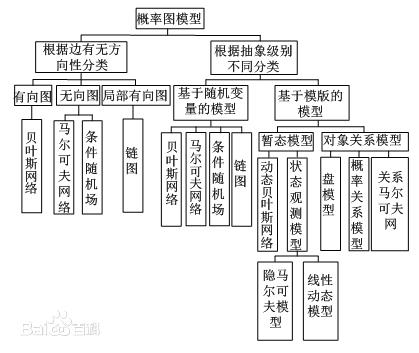
概率图模型：

有向图：贝叶斯网络NB

无向图：马尔科夫网络MM、条件随机场

局部有向图：链图

状态：动态贝叶斯网络、状态空间模型state space model（SSM）、HMM。

对象关系：概率关系GMM、关系马尔科夫网络

概率图模型主要有三个关注点：

1. 图模型的表示（representation）：指的是一个图模型应该是什么样子的；
2. 图模型的推断（inference）：指的是已知图模型的情况下，怎么去计算一个查询的概率，例如已经一些观察节点，去求其它未知节点的概率；
3. 图模型的学习（learning）：这里又分为两类，一类是图的结构学习；一类是图的参数学习。

概率图模型的理论体系如下6：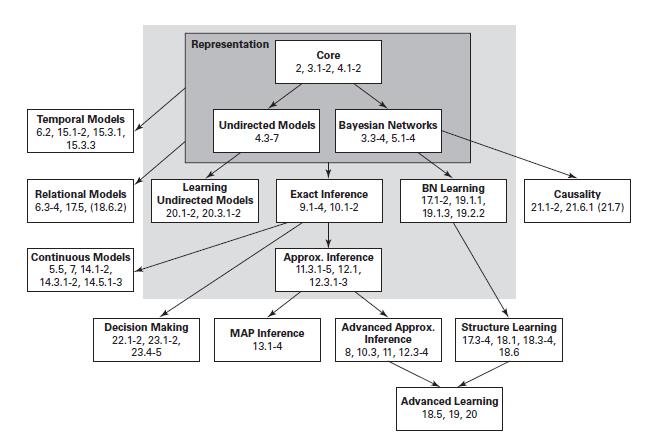

tensorflow 实现参考：

https://blog.csdn.net/u014033218/article/details/88809070